In questa lezione, mostreremo una facile strategia per risolvere il seguente problema: come trovare l’area di un triangolo isoscele.
Mettiamo in pratica alcune delle proprietà che abbiamo dimostrato finora, nel seguente problema di geometria:
Problema
In un triangolo isoscele, ΔABC, con lunghezza delle gambe 10, l’altezza alla base è uguale a due terzi della base. Trova l’area del triangolo.
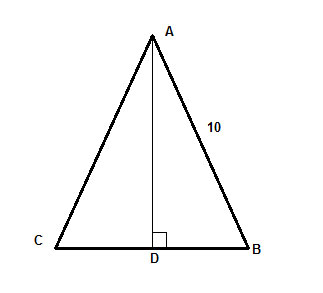
Strategia
Per risolvere questo problema, lavoreremo a ritroso da ciò che dobbiamo fare.
Dobbiamo trovare l’area del triangolo che sappiamo essere data dalla formula (base per altezza)/2.
Un problema che abbiamo è che non sappiamo né la lunghezza della base né l’altezza. Ma ci viene data la relazione tra loro, che è il suggerimento su ciò che dobbiamo fare. Chiamiamo la lunghezza della base, BC, x.
Poi sappiamo che l’altezza, AD, è 2x/3, come dato nel problema.
Quindi la risposta che stiamo cercando è (base per altezza)/2, o x per 2x/3, diviso due.
Ma come troviamo x? Ci sono due cose aggiuntive che ci sono state date nel problema e che non abbiamo ancora usato: la lunghezza della gamba (10) e il fatto che questo è un triangolo isoscele. Probabilmente dobbiamo usare queste due cose per risolvere il problema.
Ripercorriamo le proprietà dei triangoli isosceli. Una cosa che dovrebbe saltare subito alla mente è che, come abbiamo dimostrato, in un triangolo isoscele, l’altezza alla base biseca la base, quindi CD=DB=x/2.
Infine, AD è l’altezza, il che significa che l’angolo ∠ADC è un angolo retto, e abbiamo un triangolo rettangolo, ΔADC, di cui conosciamo l’ipotenusa (10) e possiamo usare per trovare le gambe usando il teorema di Pitagora, c2 =a2+b2,
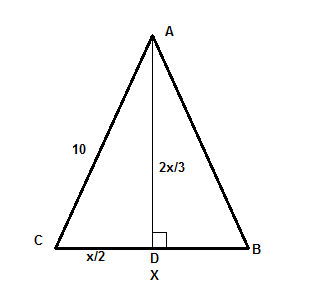
dove c= 10 , a = x/2 e b=2x/3 . E abbiamo finito, il resto è solo risolvere algebricamente per x.
Prova: area di un triangolo isoscele
(1) ΔADC è un triangolo rettangolo //dato, poiché AD è l’altezza alla base
(2) AC2 =CD2 + AD2 //Teorema di Pitagora
(3) AC= 10 //data
(4) CB = x
(5) CD = x/2 //Altezza alla base nel triangolo isoscele biseca la base
(6) AD = 2x/3 //data
(7) 102 = (x/2)2 + (2x/3)2 //Sostituire in (2)
(8) 100 = x2/4+4×2/9 //semplificare
(9) 100*36 = 9×2 +16×2 //moltiplicare entrambi i lati per 36
(10) 100*36 = 25×2 //raccogliere termini simili