Risposta 7 – 7 – 7 = 73 Si legge “sette al cubo.”

Comprendere gli esponenti e le radici quadrate

Obiettivo(i) di apprendimento

– Valutare espressioni contenenti esponenti.

– Scrivere fattori ripetuti usando la notazione esponenziale.

– Trovare la radice quadrata di un quadrato perfetto.

Gli esponenti forniscono un modo speciale di scrivere moltiplicazioni ripetute. I numeri scritti in questo modo hanno una forma specifica, con ogni parte che fornisce informazioni importanti sul numero. Scrivere i numeri usando gli esponenti può anche far risparmiare molto spazio. L’operazione inversa della moltiplicazione di un numero per se stesso si chiama trovare la radice quadrata di un numero. Questa operazione è utile per problemi sull’area di un quadrato.

La notazione esponenziale è un modo speciale di scrivere fattori ripetuti, per esempio 7 – 7. La notazione esponenziale ha due parti. Una parte della notazione è chiamata base. La base è il numero che viene moltiplicato per se stesso. L’altra parte della notazione è l’esponente, o potenza. Questo è il piccolo numero scritto in alto a destra della base. L’esponente, o potenza, dice quante volte usare la base come fattore nella moltiplicazione. Nell’esempio, 7 – 7 può essere scritto come 72, 7 è la base e 2 è l’esponente. L’esponente 2 significa che ci sono due fattori.

72 = 7 – 7 = 49

Si può leggere 72 come “sette al quadrato”. Questo perché moltiplicare un numero per se stesso si chiama “squadrare un numero”. Allo stesso modo, elevare un numero a una potenza di 3 si chiama “cubatura del numero”. Puoi leggere 73 come “sette al cubo”.

Puoi leggere 25 come “due alla quinta potenza” o “due alla potenza di cinque”. Leggete 84 come “otto alla quarta potenza” o “otto alla potenza di quattro”. Questo formato può essere usato per leggere qualsiasi numero scritto in notazione esponenziale. Infatti, mentre 63 è più comunemente letto come “sei al cubo”, può anche essere letto come “sei alla terza potenza” o “sei alla potenza di tre.”

Per trovare il valore di un numero scritto in forma esponenziale, riscrivi il numero come moltiplicazione ripetuta ed esegui la moltiplicazione. Due esempi sono mostrati sotto.

Trova il valore di 43.

A) 12

B) 64

C) 256

D) 43

Scrivere la moltiplicazione ripetuta in notazione esponenziale può risparmiare tempo e spazio. Consideriamo l’esempio 5 – 5 – 5 – 5. Possiamo usare la notazione esponenziale per scrivere questa moltiplicazione ripetuta come 54. Poiché 5 viene moltiplicato, viene scritto come base. Poiché la base è usata 4 volte nella moltiplicazione, l’esponente è 4. L’espressione 5 – 5 – 5 – 5 può essere riscritta in notazione esponenziale abbreviata come 54 e si legge, “cinque alla quarta potenza” o “cinque alla potenza di 4.”

Per scrivere la moltiplicazione ripetuta dello stesso numero in notazione esponenziale, prima scrivi il numero moltiplicato come base. Poi conta quante volte quel numero viene usato nella moltiplicazione e scrivi quel numero come esponente. Assicurati di contare i numeri, non i segni di moltiplicazione, per determinare l’esponente.

Scrivi 10 – 10 – 10 – 10 – 10 – 10 in notazione esponenziale.

A) 1.000.000

B) 60

C) 105

D) 106

Come hai visto prima, 52 è chiamato “cinque al quadrato”. “Cinque al quadrato” significa moltiplicare cinque per se stesso. In matematica, chiamiamo la moltiplicazione di un numero per se stesso “squadrare” il numero. Chiamiamo il risultato della quadratura di un numero intero un quadrato o un quadrato perfetto. Un quadrato perfetto è qualsiasi numero che può essere scritto come un numero intero elevato alla potenza di 2. Per esempio, 9 è un quadrato perfetto. Un numero perfettamente quadrato può essere rappresentato come una forma quadrata, come mostrato qui sotto. Vediamo che 1, 4, 9, 16, 25 e 36 sono esempi di quadrati perfetti.

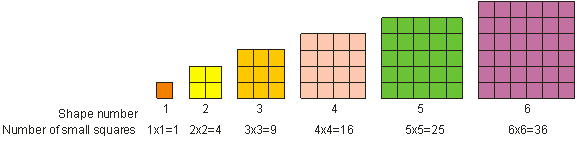
Per elevare al quadrato un numero, moltiplicare il numero per se stesso. 3 al quadrato = 32 = 3 – 3 = 9.

Di seguito ci sono altri esempi di quadrati perfetti.

L’operazione inversa di squadrare un numero si chiama trovare la radice quadrata di un numero. Trovare una radice quadrata è come chiedere: “quale numero moltiplicato per se stesso mi darà questo numero? La radice quadrata di 25 è 5, perché 5 moltiplicato per se stesso è uguale a 25. Le radici quadrate sono scritte con il simbolo matematico, chiamato segno radicale, che assomiglia a questo: . La “radice quadrata di 25” si scrive .

Cerca .

A) 6

B) 18

C) 72

D) 7

La notazione esponenziale è un modo sintetico di scrivere la moltiplicazione ripetuta dello stesso numero. Un numero scritto in notazione esponenziale ha una base e un esponente, e ciascuna di queste parti fornisce informazioni per trovare il valore dell’espressione. La base dice quale numero viene moltiplicato ripetutamente, e l’esponente dice quante volte la base viene usata nella moltiplicazione. Gli esponenti 2 e 3 hanno nomi speciali. Elevare una base a una potenza di 2 è chiamato “squadrare” un numero. Elevare una base a una potenza di 3 si chiama “cubatura” di un numero. L’inverso di squadrare un numero è trovare la radice quadrata di un numero. Per trovare la radice quadrata di un numero, chiediti: “Quale numero posso moltiplicare per se stesso per ottenere questo numero?