
La questione politica: Credito d’imposta per l’acquisto di auto ibride: è la scelta migliore del governo per ridurre il consumo di carburante e le emissioni di carbonio?
I residenti degli Stati Uniti e il governo sono preoccupati per la dipendenza dal petrolio straniero importato e il rilascio di carbonio nell’atmosfera. Nel 2005, il Congresso ha approvato una legge per fornire ai consumatori crediti d’imposta per l’acquisto di auto elettriche e ibride.
Questo credito d’imposta può sembrare una buona scelta politica, ma è costoso perché riduce direttamente la quantità di entrate che il governo degli Stati Uniti raccoglie. Ci sono approcci più efficaci per ridurre la dipendenza dai combustibili fossili e le emissioni di carbonio? Come facciamo a decidere quale politica è migliore? Per rispondere a questa domanda, i politici hanno bisogno di prevedere con una certa precisione come i consumatori risponderanno a questa politica fiscale prima che questi politici spendano milioni di dollari federali.
Possiamo applicare il concetto di utilità a questa domanda politica. In questo modulo, studieremo l’utilità e le funzioni di utilità. Saremo quindi in grado di usare una funzione di utilità appropriata per derivare curve di indifferenza che descrivono la nostra domanda politica.
Esplorare la domanda politica
Supponiamo che il credito d’imposta per sovvenzionare l’acquisto di auto ibride abbia un enorme successo e raddoppi il risparmio medio di carburante di tutte le auto sulle strade degli Stati Uniti – un risultato che non è chiaramente realistico ma utile per le nostre discussioni successive. Cosa pensate che succederebbe al consumo di carburante di tutti gli automobilisti statunitensi? Il governo dovrebbe aspettarsi che il consumo di carburante e le emissioni di carbonio delle auto diminuiscano della metà in risposta? Perché o perché no?
2.1 Funzioni di utilità
LO 2.1: Descrivere una funzione di utilità.
2.2 Funzioni di utilità e preferenze tipiche
LO 2.2: Identificare le funzioni di utilità in base alle preferenze tipiche che rappresentano.
2.3 Mettere in relazione le funzioni di utilità e le mappe delle curve di indifferenza
LO 2.3: Spiegare come derivare una curva di indifferenza da una funzione di utilità.
2.4 Trovare l’utilità marginale e il tasso marginale di sostituzione
LO 2.4: Derivare l’utilità marginale e il tasso di sostituzione per funzioni di utilità tipiche.
2.5. Domanda politica
2.1 Funzioni di utilità
LO1: Descrivere una funzione di utilità.
Le nostre preferenze ci permettono di fare confronti tra diversi pacchetti di consumo e scegliere i pacchetti preferiti. Potremmo, per esempio, determinare l’ordine di rango di un intero insieme di pacchetti in base alle nostre preferenze. Una funzione di utilità è una funzione matematica che classifica i pacchetti di beni di consumo assegnando un numero a ciascuno di essi, dove i numeri più grandi indicano i pacchetti preferiti. Le funzioni di utilità hanno le proprietà che abbiamo identificato nel Modulo 1 riguardo alle preferenze. Cioè: sono in grado di ordinare i pacchetti, sono complete e transitive, più è preferito a meno e, in casi rilevanti, i pacchetti misti sono migliori.
Il numero che la funzione di utilità assegna a un pacchetto specifico è noto come utilità, la soddisfazione che un consumatore ottiene da un pacchetto specifico. Il numero di utilità per ogni pacchetto non significa nulla in termini assoluti; non c’è una scala uniforme con cui misuriamo la soddisfazione. Il suo unico scopo è in termini relativi: possiamo usare l’utilità per determinare quali pacchetti sono preferiti ad altri.
Se l’utilità del pacchetto A è superiore all’utilità del pacchetto B, è equivalente a dire che un consumatore preferisce il pacchetto A al pacchetto B. Le funzioni di utilità quindi classificano le preferenze dei consumatori assegnando un numero a ciascun pacchetto. . Possiamo usare una funzione di utilità per disegnare le mappe delle curve di indifferenza descritte nel Modulo 1. Poiché tutti i pacchetti sulla stessa curva di indifferenza forniscono la stessa soddisfazione, e quindi nessuno è preferito, ogni pacchetto ha la stessa utilità. Possiamo quindi disegnare una curva di indifferenza determinando tutti i pacchetti che restituiscono lo stesso numero dalla funzione di utilità.
Gli economisti dicono che le funzioni di utilità sono ordinali piuttosto che cardinali. Ordinale significa che le funzioni di utilità classificano solo i pacchetti – indicano solo quale è migliore, non quanto sia migliore di un altro pacchetto. Supponiamo, per esempio, che una funzione di utilità indichi che il pacchetto A restituisce 10 utils e il pacchetto B 20 utils. Non diciamo che il pacchetto B è due volte più buono, o 10 utils meglio, solo che il consumatore preferisce il pacchetto B. Per esempio, supponiamo che un’amica abbia partecipato a una gara e vi abbia detto che è arrivata terza. Questa informazione è ordinale: Sapete che era più veloce del quarto classificato e più lento del secondo. Conoscete solo l’ordine in cui i corridori hanno finito. I tempi individuali sono cardinali: Se il primo classificato ha corso la gara esattamente in un’ora e il tuo amico ha finito in un’ora e sei minuti, sai che il tuo amico era esattamente il 10% più lento del corridore più veloce. Questo è vero finché l’ordinamento è conservato.
Prendiamo per esempio la funzione di utilità U che descrive le preferenze sui pacchetti di beni A e B: U(A,B). Possiamo applicare qualsiasi trasformazione monotona positiva a questa funzione (il che significa, essenzialmente, che non cambiamo l’ordinamento) e la nuova funzione che abbiamo creato rappresenterà le stesse preferenze. Per esempio, potremmo moltiplicare una costante positiva, α , o aggiungere una costante positiva o negativa, β . Quindi αU(A,B)+β rappresenta esattamente le stesse preferenze di U(A,B) perché ordinerà i fasci esattamente nello stesso modo. Questo fatto è abbastanza utile perché a volte applicare una trasformazione monotona positiva di una funzione di utilità rende più facile risolvere i problemi.
2.2 Funzioni di utilità e preferenze tipiche
LO2: Identificare le funzioni di utilità in base alle preferenze tipiche che rappresentano
Considera i fasci di mele, A, e di banane, B. Una funzione di utilità che descrive le preferenze di Isaac per i fasci di mele e banane è la funzione U(A,B). Ma quali sono le particolari preferenze di Isaac per i pacchetti di mele e banane? Supponiamo che Isaac abbia delle preferenze abbastanza standard per mele e banane che portano alle nostre tipiche curve di indifferenza: Preferisce di più a meno, e gli piace la varietà. Una funzione di utilità che rappresenti queste preferenze potrebbe essere:
U(A,B) = AB
Se le mele e le banane sono complementi perfetti nelle preferenze di Isaac, la funzione di utilità sarebbe qualcosa come questa:
U(A,B) = MIN,
dove la funzione MIN assegna semplicemente il più piccolo dei due numeri come valore della funzione.
Se le mele e le banane sono sostituti perfetti, la funzione di utilità è additiva e assomiglierebbe a questa:
U(A,B) = A + B
Una classe di funzioni di utilità conosciute come funzioni di utilità Cobb-Douglas sono molto usate in economia per due ragioni:
1. Rappresentano preferenze ‘ben educate’, come più è meglio e la preferenza per la varietà.
2. Sono molto flessibili e possono essere adattate molto facilmente ai dati del mondo reale.
Le funzioni di utilità di Coop-Douglas hanno questa forma:
U(A,B) = AαBβ
Perché le trasformazioni monotoniche positive rappresentano le stesse preferenze, una di queste trasformazioni può essere usata per impostare α + β = 1, che più avanti vedremo essere una condizione conveniente che semplifica alcuni calcoli nel problema della scelta del consumatore.
Un altro modo per trasformare la funzione di utilità in modo utile è prendere il log naturale della funzione, che crea una nuova funzione che assomiglia a questa:
U(A,B) = αln(A) + βln(B)
Per ricavare questa equazione, basta applicare le regole dei log naturali. È importante tenere a mente il livello di astrazione qui. In genere non possiamo creare funzioni di utilità specifiche che descrivano precisamente le preferenze individuali. Probabilmente nessuno di noi potrebbe descrivere le proprie preferenze con una singola equazione. Ma finché i consumatori in generale hanno preferenze che seguono le nostre ipotesi di base, possiamo fare un buon lavoro nel trovare funzioni di utilità che corrispondano ai dati di consumo del mondo reale. Ne vedremo la prova più avanti nel corso.
La tabella 2.1 riassume le preferenze e le funzioni di utilità descritte in questa sezione.
|
Tabella 2.1 Tipi di preferenze e funzioni di utilità che le rappresentano |
||
|
PREFERENZE |
UTILITÀ FUNZIONE |
Tipo di funzione di utilità |
|
Amore della varietà o “ben educato” |
U(A,B) = AB |
Cobb-Douglas |
|
Amore per la varietà o “ben educato” |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Amore della varietà o “ben educato” |
U(A,B) = αln(A) + βln(B) |
Naturale Log Cobb-Douglas |
|
Complementi perfetti |
U(A,B) = MIN |
Funzione Min |
|
Sostituti perfetti |
U(A,B) = A + B |
Additivo |
2.3 Mettere in relazione funzioni di utilità e mappe di curve di indifferenza
LO3: Spiegare come derivare una curva di indifferenza da una funzione di utilità
Le curve di indifferenza e le funzioni di utilità sono direttamente correlate. Infatti, poiché le curve di indifferenza rappresentano le preferenze graficamente e le funzioni di utilità rappresentano le preferenze matematicamente, ne consegue che le curve di indifferenza possono essere derivate dalle funzioni di utilità.
Nelle funzioni uni-variate, la variabile dipendente è tracciata sull’asse verticale e la variabile indipendente è tracciata sull’asse orizzontale, come il grafico di y=f(x). Al contrario, i grafici delle funzioni bi-variate sono tridimensionali, come U=U(A,B). La figura 2.1 mostra un grafico di U=A^\frac{1}{2}B^\frac{1}{2}. I grafici tridimensionali sono utili per capire come l’utilità aumenta con l’aumento del consumo sia di A che di B.
Figura 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
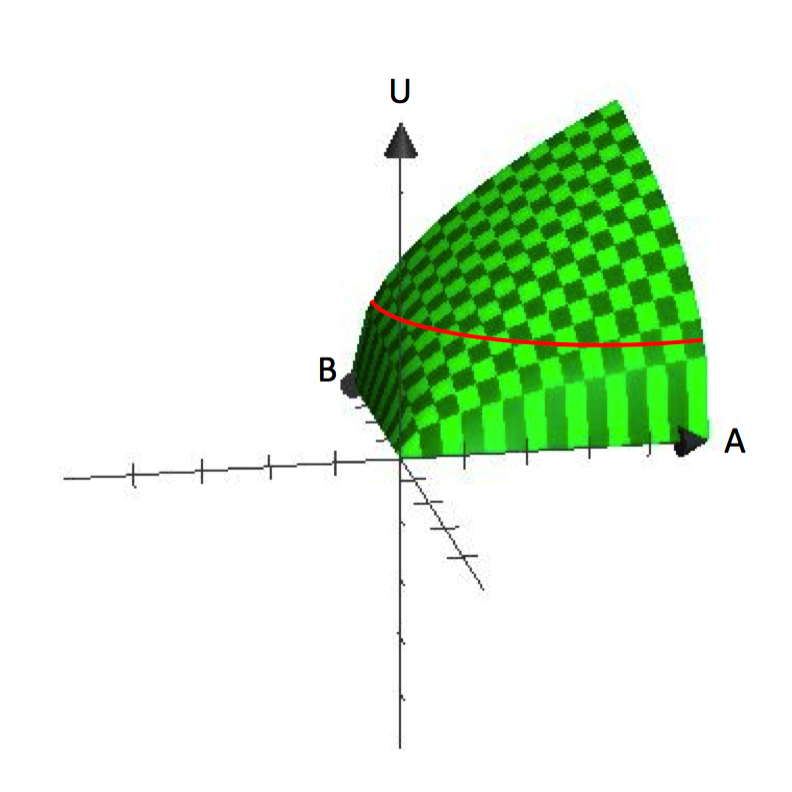
La figura 2.1 mostra chiaramente il presupposto che i consumatori hanno una preferenza per la varietà. Ogni mazzo che contiene una quantità specifica di A e B rappresenta un punto sulla superficie. L’altezza verticale della superficie rappresenta il livello di utilità. Aumentando sia A che B, un consumatore può raggiungere punti più alti sulla superficie.
Da dove vengono le curve di indifferenza? Ricordiamo che una curva di indifferenza è un insieme di tutti i pacchetti per i quali un consumatore è indifferente, rispetto a quale consumare. Matematicamente, questo equivale a dire che tutti i pacchetti, se messi nella funzione di utilità, restituiscono lo stesso valore funzionale. Quindi, se fissiamo un valore per l’utilità, Ū, e troviamo tutti i bundle di A e B che generano quel valore, definiremo una curva di indifferenza. Notate che questo equivale a trovare tutti i pacchetti che portano il consumatore alla stessa altezza sulla superficie tridimensionale nella figura 2.1.
Le curve di indifferenza sono una rappresentazione dell’elevazione (livello di utilità) su una superficie piatta. In questo modo, sono analoghe a una linea di contorno su una mappa topografica. Riportando il grafico tridimensionale allo spazio bidimensionale – lo spazio A, B – possiamo mostrare le linee di contorno/curve di differenza che rappresentano diverse elevazioni o livelli di utilità. Dal grafico in figura 2.1, si può già vedere come questa funzione di utilità produce curve di indifferenza che sono ‘bowed-in’ o concave verso l’origine.
Quindi le curve di indifferenza seguono direttamente dalle funzioni di utilità e sono un modo utile per rappresentare le funzioni di utilità in un grafico bidimensionale.
2.4 Trovare l’utilità marginale e il tasso marginale di sostituzione
LO4: Derivare l’utilità marginale e l’MRS per funzioni di utilità tipiche.
L’utilità marginale è l’utilità addizionale che un consumatore riceve dal consumo di una unità addizionale di un bene. Matematicamente la esprimiamo come:
MU_{a}=frac{Delta \cup }{Delta A}
ovvero il cambiamento di utilità da un cambiamento nella quantità di A consumata, dove Δ rappresenta un cambiamento nel valore del bene. Quindi,
MU_{a}=frac{Delta \cup }{Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Nota che quando stiamo esaminando l’utilità marginale del consumo di A, teniamo B costante.
Utilizzando il calcolo, l’utilità marginale è uguale alla derivata parziale della funzione di utilità rispetto ad A:
MU_{A}frac{parziale U(A,B)}{parziale A}
Consideriamo un consumatore che si siede a mangiare un pasto di insalata e pizza. Supponiamo di mantenere costante la quantità di insalata – un contorno di insalata con una cena, per esempio. Ora aumentiamo le fette di pizza, supponiamo che con 1 fetta l’utilità sia 10, con 2 è 18, con 3 è 24 e con 4 è 28. Tracciamo questi numeri su un grafico che ha l’utilità sull’asse verticale e la pizza sull’asse orizzontale (Figura 2.2).
Figura 2.2: Grafico e tabella dell’utilità marginale decrescente
|
Fette di pizza |
Utilità |
Marginale Utilità |
|
1 |
10 |
|
|
2 |
18 |
8 |
|
3 |
24 |
6 |
|
4 |
28 |
4 |
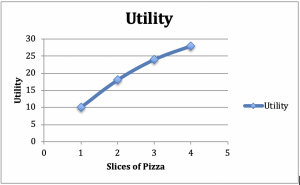
Dalla pendenza positiva del grafico, possiamo vedere l’aumento dell’utilità da fette di pizza aggiuntive. Dalla forma concava del grafico, possiamo vedere un altro fenomeno comune: L’utilità aggiuntiva che il consumatore riceve da ogni fetta di pizza aggiuntiva diminuisce con il numero di fette consumate.
Il fatto che l’utilità aggiuntiva diventa più piccola con ogni fetta di pizza aggiuntiva è chiamato principio di utilità marginale decrescente. Questo principio si applica alle preferenze ben educate in cui i pacchetti misti sono preferiti.
Il tasso marginale di sostituzione (MRS) è la quantità di un bene a cui un consumatore è disposto a rinunciare per ottenere una unità in più di un altro bene. Questo è il motivo per cui è la stessa cosa della pendenza della curva di indifferenza – dal momento che manteniamo costante il livello di soddisfazione, rimaniamo sulla stessa curva di indifferenza, solo spostandoci lungo di essa mentre scambiamo un bene per un altro. Quanto di un bene si è disposti a scambiare per uno in più di un altro dipende dall’utilità marginale di ciascuno.
Utilizzando il nostro esempio precedente, se consumando un lato di insalata in più la tua utilità sale di 10, allora con un consumo attuale di 4 fette di pizza, potresti rinunciare a 2 fette di pizza e passare da 28 a 18 utils. 10 utils in più dall’insalata e 10 utils in meno rinunciando a 2 fette di pizza lasciano l’utilità complessiva invariata – quindi dobbiamo essere ancora sulla stessa curva di indifferenza. Mentre ci si muove lungo la curva di indifferenza, si deve cavalcare la pendenza, cioè si deve rinunciare al bene sull’asse verticale in cambio di più del bene sull’asse orizzontale, il che produce un aumento negativo su una corsa positiva.
Possiamo passare direttamente dall’utilità marginale alla MRS riconoscendo la connessione tra i due concetti. Nel nostro caso, per una funzione di utilità U=U(A,B) , la MRS è rappresentata come:
MRS=-\frac{MU_{A}{MU_{B}}
Nota che quando sostituiamo possiamo semplificare l’equazione:
MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{Delta U}{Delta A}}{\frac{Delta U}{Delta B}}=-\frac{Delta B}{Delta A}
Inserendo il calcolo equivale a:
MRS=-\frac{frac{parziale U(A,B)}{parziale A}}{frac{parziale U(A,B)}{parziale B}
2.5 Domanda politica
Abbiamo determinato nel Modulo 1 che la decisione del consumatore tra più chilometri percorsi e altri consumi probabilmente è conforme alle ipotesi standard sulla scelta del consumatore. Quindi, usare la funzione di utilità Cobb-Douglas per rappresentare un consumatore a cui piace guidare un’auto e consumare altri beni, e che li vede come un trade-off (il denaro speso per la benzina è denaro non speso per altri beni di consumo), è una buona scelta. Ha anche i vantaggi di essere sia conforme alle ipotesi, sia flessibile:
U(MD,C)=MD^{a}C^{\beta }
dove MD = miglia percorse, e C = altri consumi.
In effetti, la funzione stessa può essere portata ai dati del mondo reale dove i parametri e possono essere stimati per questo mercato, il mercato dei chilometri percorsi nell’auto del consumatore.
Figura 2.3 Grafico delle curve di indifferenza per l’esempio di politica
Esplorazione delle domande sulla politica:
1 . Altri tipi di preferenza sarebbero più appropriati in questo esempio?
2. Cosa dovrebbe essere vero per i complementi perfetti per essere il tipo di preferenza appropriato da usare per analizzare questa politica?
Cosa dovrebbe essere vero per i sostituti perfetti? 3. Dato che stiamo considerando un consumatore ‘tipico’ che guida, è appropriato scegliere una funzione di utilità ‘tipica’?
4. Stiamo solo tirando a indovinare o abbiamo qualche base teorica per sostenere la nostra scelta di preferenze ‘ben educate’ o una funzione di utilità Cobb-Douglas?
SOMMARIO
Rassegna: Argomenti e risultati di apprendimento correlati
2.1 Funzioni di utilità
LO 2.1: Descrivere una funzione di utilità
2.2 Funzioni di utilità e preferenze tipiche
LO 2.2: Identificare le funzioni di utilità in base alle preferenze tipiche che rappresentano
2.3 Mettere in relazione le funzioni di utilità e le mappe delle curve di indifferenza
LO 2.3: Spiegare come derivare una curva di indifferenza da una funzione di utilità
2.4 Trovare l’utilità marginale e il tasso marginale di sostituzione
LO 2.4: Derivare l’utilità marginale e il tasso marginale di sostituzione per funzioni di utilità tipiche.
2.5. Domanda politica
Impara: Termini chiave e grafici
Funzioni bi-funzioni variabili
Cardinale
Retta di contorno
Utilità marginale decrescente
Funzione
Tasso marginale di sostituzione (MRS)
Utilità marginale
Ordinale
Funzioni univariate
Util
Utilità
Funzione di utilità
Grafi
Funzione di utilità 3D e curva di livello
Equazioni
Cobb-Douglas
Complementi perfetti
Sostituti perfetti