La deviazione standard è la quantità media di variabilità nel vostro set di dati. Ti dice, in media, quanto ogni valore si trova lontano dalla media.
Un’alta deviazione standard significa che i valori sono generalmente lontani dalla media, mentre una bassa deviazione standard indica che i valori sono raggruppati vicino alla media.
Cosa ti dice la deviazione standard?
La deviazione standard è un’utile misura della diffusione per le distribuzioni normali.
Nelle distribuzioni normali, i dati sono distribuiti simmetricamente senza asimmetria. La maggior parte dei valori si raggruppa intorno a una regione centrale, con valori che si assottigliano man mano che si allontanano dal centro. La deviazione standard vi dice quanto i vostri dati sono mediamente distanti dal centro della distribuzione.
Molte variabili scientifiche seguono distribuzioni normali, compresa l’altezza, i punteggi dei test standardizzati o le valutazioni di soddisfazione sul lavoro. Quando hai le deviazioni standard di diversi campioni, puoi confrontare le loro distribuzioni usando test statistici per fare inferenze sulle popolazioni più grandi da cui provengono.
Le valutazioni medie (M) sono le stesse per ogni gruppo – è il valore sull’asse x quando la curva è al suo picco. Tuttavia, le loro deviazioni standard (SD) differiscono l’una dall’altra.
La deviazione standard riflette la dispersione della distribuzione. La curva con la deviazione standard più bassa ha un picco alto e una piccola diffusione, mentre la curva con la deviazione standard più alta è più piatta e diffusa.
La regola empirica
La deviazione standard e la media insieme possono dirti dove si trova la maggior parte dei valori nella tua distribuzione se seguono una distribuzione normale.
La regola empirica, o la regola 68-95-99.7, ti dice dove si trovano i tuoi valori:
- Circa il 68% dei punteggi sono entro 2 deviazioni standard della media,
- Circa il 95% dei punteggi sono entro 4 deviazioni standard della media,
- Circa il 99.7% dei punteggi sono entro 6 deviazioni standard della media.
Seguendo la regola empirica:
- Circa il 68% dei punteggi sono tra 40 e 60.
- Circa il 95% dei punteggi sono tra 30 e 70.
- Circa il 99,7% dei punteggi è compreso tra 20 e 80.
La regola empirica è un modo veloce per avere una visione d’insieme dei tuoi dati e controllare eventuali outlier o valori estremi che non seguono questo schema.
Per distribuzioni non normali, la deviazione standard è una misura meno affidabile della variabilità e dovrebbe essere usata in combinazione con altre misure come l’intervallo o l’intervallo interquartile.
Formule di deviazione standard per popolazioni e campioni
Per calcolare le deviazioni standard si usano formule diverse a seconda che si abbiano dati di un’intera popolazione o di un campione.
Deviazione standard della popolazione
Quando hai raccolto dati da ogni membro della popolazione che ti interessa, puoi ottenere un valore esatto per la deviazione standard della popolazione.
La formula della deviazione standard della popolazione si presenta così:
| Formula | Spiegazione |
|---|---|
 |
|
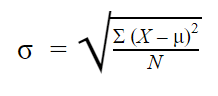Deviazione standard del campione
Quando si raccolgono dati da un campione, la deviazione standard del campione è usata per fare stime o inferenze sulla deviazione standard della popolazione.
La formula della deviazione standard del campione si presenta così:
| Formula | Spiegazione |
|---|---|
 |
|
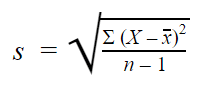Con i campioni, usiamo n – 1 nella formula perché usando n avremmo una stima distorta che sottostima costantemente la variabilità. La deviazione standard del campione tenderebbe ad essere più bassa della reale deviazione standard della popolazione.
Riducendo il campione n a n – 1 si rende la deviazione standard artificialmente grande, dando una stima conservativa della variabilità.
Anche se questa non è una stima imparziale, è una stima meno distorta della deviazione standard: è meglio sovrastimare piuttosto che sottostimare la variabilità nei campioni.
Passi per calcolare la deviazione standard
La deviazione standard è solitamente calcolata automaticamente dal software che usi per le tue analisi statistiche. Ma puoi anche calcolarla a mano per capire meglio come funziona la formula.
Ci sono sei passi principali per trovare la deviazione standard a mano. Utilizzeremo un piccolo set di dati di 6 punteggi per illustrare i passi.
| Set di dati | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Passo 1: Trova la media
Per trovare la media, somma tutti i punteggi, poi dividili per il numero di punteggi.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Passo 2: Trova la deviazione di ogni punteggio dalla media
Sottrai la media da ogni punteggio per ottenere le deviazioni dalla media.
Siccome x̅ = 50, qui togliamo 50 da ogni punteggio.
| Score | Deviazione dalla media |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Passo 3: Elevare al quadrato ogni deviazione dalla media
Moltiplicare ogni deviazione dalla media per se stessa. Questo risulterà in numeri positivi.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Passo 4: Trova la somma dei quadrati
Aggiungi tutte le deviazioni al quadrato. Questa è chiamata la somma dei quadrati.
16 + 361 + 324 + 100 + 4 + 81 = 886
Passo 5: Trova la varianza
Dividi la somma dei quadrati per n – 1 (per un campione) o N (per una popolazione) – questa è la varianza.
Siccome stiamo lavorando con un campione di 6, useremo n – 1, dove n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Passo 6: Trovare la radice quadrata della varianza
Per trovare la deviazione standard, prendiamo la radice quadrata della varianza.
√177.2 = 13.31
Dall’apprendimento che SD = 13.31, possiamo dire che ogni punteggio si discosta dalla media di 13,31 punti in media.
Perché la deviazione standard è una misura utile della variabilità?
Anche se ci sono modi più semplici per calcolare la variabilità, la formula della deviazione standard pesa di più i campioni distribuiti in modo irregolare che quelli distribuiti in modo uniforme. Una deviazione standard più alta ti dice che la distribuzione non solo è più diffusa, ma anche più disomogenea.
Questo significa che ti dà un’idea migliore della variabilità dei tuoi dati rispetto a misure più semplici, come la deviazione assoluta media (MAD).
La MAD è simile alla deviazione standard ma più facile da calcolare. Per prima cosa, si esprime ogni deviazione dalla media in valori assoluti convertendoli in numeri positivi (per esempio, -3 diventa 3). Poi, si calcola la media di queste deviazioni assolute.
A differenza della deviazione standard, non è necessario calcolare i quadrati o le radici quadrate dei numeri per la MAD. Tuttavia, per questa ragione, vi dà una misura meno precisa della variabilità.
Prendiamo due campioni con la stessa tendenza centrale ma con diverse quantità di variabilità. Il campione B è più variabile del campione A.
| Valori | Media | Deviazione assoluta media | Deviazione standard | |
|---|---|---|---|---|
| Campione A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| Campione B | 51, 21, 79, 49 | 50 | 15 | 23.7 |
Per campioni con deviazioni medie uguali dalla media, la MAD non può distinguere i livelli di diffusione. La deviazione standard è più precisa: è più alta per il campione con più variabilità nelle deviazioni dalla media.
Quadrando le differenze dalla media, la deviazione standard riflette più accuratamente la dispersione irregolare. Questo passo pesa le deviazioni estreme più pesantemente delle piccole deviazioni.
Tuttavia, questo rende anche la deviazione standard sensibile agli outlier.
Domande frequenti sulla deviazione standard
La variabilità è più comunemente misurata con le seguenti statistiche descrittive:
- Range: la differenza tra il valore più alto e quello più basso
- Range interquartile: la gamma della metà centrale di una distribuzione
- Deviazione standard: distanza media dalla media
- Varianza: media delle distanze quadrate dalla media
La deviazione standard è la quantità media di variabilità nella tua serie di dati. Ti dice, in media, quanto ogni punteggio si trova lontano dalla media.
Nelle distribuzioni normali, una deviazione standard alta significa che i valori sono generalmente lontani dalla media, mentre una deviazione standard bassa indica che i valori sono raggruppati vicino alla media.
In una distribuzione normale, i dati sono distribuiti simmetricamente senza asimmetrie. La maggior parte dei valori si raggruppa intorno a una regione centrale, con valori che si assottigliano man mano che si allontanano dal centro.
Le misure di tendenza centrale (media, modo e mediana) sono esattamente le stesse in una distribuzione normale.
La regola empirica, o la regola 68-95-99.7, ti dice dove si trova la maggior parte dei valori in una distribuzione normale:
- Circa il 68% dei valori sono entro 1 deviazione standard della media.
- Circa il 95% dei valori sono entro 2 deviazioni standard della media.
- Circa il 99.Il 7% dei valori sono entro 3 deviazioni standard della media.
La regola empirica è un modo veloce per avere una visione d’insieme dei tuoi dati e controllare eventuali outlier o valori estremi che non seguono questo schema.
La varianza è la media delle deviazioni al quadrato dalla media, mentre la deviazione standard è la radice quadrata di questo numero. Entrambe le misure riflettono la variabilità in una distribuzione, ma le loro unità differiscono:
- La deviazione standard è espressa nelle stesse unità dei valori originali (ad esempio, minuti o metri).
- La varianza è espressa in unità molto più grandi (ad esempio, metri al quadrato).
Anche se le unità della varianza sono più difficili da capire intuitivamente, la varianza è importante nei test statistici.