
Lo studioso greco classico Aristotele (384-322 a.C.) fu il primo a dedicare seria attenzione agli arcobaleni. Secondo Raymond L. Lee e Alistair B. Fraser, “Nonostante i suoi molti difetti e il suo appello alla numerologia pitagorica, la spiegazione qualitativa di Aristotele ha mostrato un’inventiva e una relativa coerenza che non ha avuto eguali per secoli. Dopo la morte di Aristotele, gran parte delle teorie sull’arcobaleno consistevano in reazioni al suo lavoro, anche se non tutte erano acritiche.”
Nel libro I delle Naturales Quaestiones (65 d.C. circa), il filosofo romano Seneca il Giovane discute a lungo varie teorie sulla formazione dell’arcobaleno, comprese quelle di Aristotele. Egli nota che gli arcobaleni appaiono sempre di fronte al sole, che appaiono nell’acqua spruzzata da un rematore, nell’acqua sputata da una frusta su vestiti tesi da pinze, o nell’acqua spruzzata attraverso un piccolo foro in un tubo scoppiato. Ha anche parlato di arcobaleni prodotti da piccole bacchette di vetro (virgulae), anticipando gli esperimenti di Newton con i prismi. Aveva due teorie in mente: una, che l’arcobaleno fosse prodotto dal sole che rifletteva ogni goccia d’acqua; e l’altra, che fosse prodotto dal sole che rifletteva una nuvola a forma di specchio concavo; favorì la seconda. Discusse anche altri fenomeni legati all’arcobaleno: le misteriose “virgas” (aste), gli aloni e i parhelia.
Secondo Hüseyin Gazi Topdemir, il fisico e polimaco arabo Ibn al-Haytham (Alhazen; 965-1039), tentò di fornire una spiegazione scientifica al fenomeno dell’arcobaleno. Nella sua Maqala fi al-Hala wa Qaws Quzah, al-Haytham “ha spiegato la formazione dell’arcobaleno come un’immagine che si forma in uno specchio concavo. Se i raggi di luce provenienti da una fonte di luce più lontana si riflettono in un punto qualsiasi dell’asse dello specchio concavo, formano cerchi concentrici in quel punto. Quando si assume il sole come ulteriore fonte di luce, l’occhio dello spettatore come un punto sull’asse dello specchio e una nuvola come superficie riflettente, allora si può osservare che sull’asse si formano dei cerchi concentrici”. Non poteva verificarlo perché la sua teoria che “la luce del sole viene riflessa da una nuvola prima di raggiungere l’occhio” non permetteva una possibile verifica sperimentale. Questa spiegazione fu ripetuta da Averroè e, sebbene errata, fornì la base per le spiegazioni corrette date più tardi da Kamāl al-Dīn al-Fārisī nel 1309 e, indipendentemente, da Teodorico di Freiberg (circa 1250 – circa 1311) – entrambi i quali avevano studiato il Libro di Ottica di al-Haytham.
Un contemporaneo di Ibn al-Haytham, il filosofo e studioso persiano Ibn Sīnā (Avicenna, 980-1037), ha fornito una spiegazione alternativa: “che l’arco non si forma nella nuvola scura ma piuttosto nella nebbia molto fine che si trova tra la nuvola e il sole o l’osservatore. La nuvola, pensò, serve solo come sfondo per questa sostanza sottile, proprio come quando un rivestimento di mercurio è posto sulla superficie posteriore del vetro in uno specchio. Ibn Sīnā sposterebbe il luogo non solo dell’arco, ma anche della formazione del colore, ritenendo che l’iridescenza sia semplicemente una sensazione soggettiva dell’occhio”. Anche questa spiegazione, però, non era corretta. Il resoconto di Ibn Sīnā accettava molti degli argomenti di Aristotele sugli arcobaleni.
Nella Cina della dinastia Song (960-1279), un polimatico e studioso ufficiale di nome Shen Kuo (1031-1095) ipotizzò – come aveva fatto in precedenza un certo Sun Sikong (1015-1076) – che gli arcobaleni fossero formati da un fenomeno di luce solare che incontra le gocce di pioggia in aria. Paul Dong sottolinea che la spiegazione di Shen dell’arcobaleno come fenomeno di rifrazione atmosferica “è fondamentalmente in accordo con i principi scientifici moderni”.
Secondo Nader El-Bizri, l’astronomo persiano Qutb al-Din al-Shirazi (1236-1311), ha dato una spiegazione abbastanza precisa del fenomeno dell’arcobaleno. Questo fu elaborato dal suo allievo, Kamāl al-Dīn al-Fārisī (1267-1319), che diede una spiegazione più matematicamente soddisfacente dell’arcobaleno. “Egli propose un modello in cui il raggio di luce del sole veniva rifratto due volte da una goccia d’acqua, con una o più riflessioni che si verificavano tra le due rifrazioni. Un esperimento fu condotto con una sfera di vetro riempita d’acqua e al-Farisi dimostrò che le rifrazioni aggiuntive dovute al vetro potevano essere ignorate nel suo modello. Come notato nel suo Kitab Tanqih al-Manazir , al-Farisi ha usato un grande recipiente di vetro trasparente a forma di sfera, che è stato riempito con acqua, per avere un modello sperimentale su larga scala di una goccia di pioggia. Ha poi messo questo modello in una camera buia che aveva un’apertura controllata per far passare la luce. Proiettò la luce sulla sfera e alla fine dedusse, attraverso vari test e osservazioni dettagliate delle riflessioni e rifrazioni della luce, che i colori dell’arcobaleno erano fenomeni di decadimento della luce.
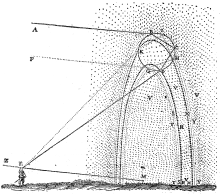
In Europa, il Libro di ottica di Ibn al-Haytham fu tradotto in latino e studiato da Robert Grosseteste. Il suo lavoro sulla luce fu continuato da Roger Bacon, che scrisse nel suo Opus Majus del 1268 di esperimenti con la luce che brilla attraverso cristalli e gocce d’acqua che mostrano i colori dell’arcobaleno. Inoltre, Bacon fu il primo a calcolare la dimensione angolare dell’arcobaleno. Ha dichiarato che la parte superiore dell’arcobaleno non può apparire più di 42° sopra l’orizzonte. Teodorico di Freiberg è noto per aver dato un’accurata spiegazione teorica degli arcobaleni primari e secondari nel 1307 (poi sviluppata da Antonius de Demini nel 1611). Ha spiegato l’arcobaleno primario, notando che “quando la luce del sole cade su singole gocce di umidità, i raggi subiscono due rifrazioni (entrando e uscendo) e una riflessione (sul retro della goccia) prima della trasmissione all’occhio dell’osservatore”. Ha spiegato l’arcobaleno secondario attraverso un’analisi simile che coinvolge due rifrazioni e due riflessioni.
René Descartes, nel suo trattato del 1637, Discorso sul metodo, avanzò ulteriormente questa spiegazione. Sapendo che la dimensione delle gocce di pioggia non sembrava influenzare l’arcobaleno osservato, sperimentò il passaggio dei raggi di luce attraverso una grande sfera di vetro piena d’acqua. Misurando gli angoli in cui i raggi emergevano, concluse che l’arco primario era causato da una singola riflessione interna alla goccia di pioggia e che l’arco secondario poteva essere causato da due riflessioni interne. Ha sostenuto questa conclusione con una derivazione della legge della rifrazione (successiva, ma indipendente dalla legge di Snell) e ha calcolato correttamente gli angoli per entrambi gli archi. Tuttavia, la sua spiegazione dei colori era basata su una versione meccanica della teoria tradizionale che i colori erano prodotti da una modifica della luce bianca.
Isaac Newton dimostrò che la luce bianca era composta dalla luce di tutti i colori dell’arcobaleno, che un prisma di vetro poteva separare nell’intero spettro dei colori – decomposizione della luce bianca – rifiutando la teoria che i colori erano prodotti da una modifica della luce bianca. Mostrò anche che la luce rossa si rifrangeva meno della luce blu, portando alla prima spiegazione scientifica delle principali caratteristiche dell’arcobaleno. La teoria corpuscolare della luce di Newton non era in grado di spiegare gli arcobaleni soprannumerari, per i quali non fu trovata alcuna spiegazione soddisfacente fino a quando Thomas Young si rese conto che la luce si comportava come un’onda in certe condizioni e poteva interferire con se stessa.
Il lavoro di Young, successivamente elaborato in dettaglio da Richard Potter, fu perfezionato negli anni 1820 da George Biddell Airy, che spiegò che esisteva una dipendenza tra la forza dei colori dell’arcobaleno e la dimensione delle gocce d’acqua. Le moderne descrizioni fisiche degli arcobaleni si basano sulla dispersione di Mie, pubblicata da Gustav Mie nel 1908. I progressi nei metodi computazionali e nella teoria ottica continuano a portare a una comprensione più completa degli arcobaleni. Per esempio, Nussenzveig fornisce una panoramica moderna.

.