A Concise Introduction to Logic

9.1 Un esempio storico

Il filosofo David Hume (1711-1776) è ricordato per essere un brillante empirista scettico. Una persona è scettica su un argomento se ha standard molto severi per ciò che costituisce la conoscenza su quell’argomento e crede anche che non possiamo soddisfare questi standard severi. L’empirismo è il punto di vista che noi otteniamo la conoscenza principalmente attraverso l’esperienza, in particolare le esperienze dei nostri sensi. Nel suo libro, An Inquiry Concerning Human Understanding, Hume espone i suoi principi per la conoscenza, e poi ci consiglia di ripulire le nostre biblioteche:

Quando corriamo sulle biblioteche, persuasi di questi principi, che disastro dobbiamo fare? Se prendiamo in mano un qualsiasi volume di divinità o di metafisica scolastica, per esempio, chiediamoci: contiene qualche ragionamento astratto sulla quantità o sul numero? No. Contiene qualche ragionamento sperimentale sulla materia di fatto e sull’esistenza? No. Affidatelo allora alle fiamme, perché non può contenere altro che sofismi e illusioni.

Hume ritiene che le uniche fonti di conoscenza siano il ragionamento logico o matematico (che egli chiama sopra “ragionamento astratto riguardante la quantità o il numero”) o l’esperienza dei sensi (“ragionamento sperimentale riguardante la materia dei fatti e dell’esistenza”). Hume è portato a sostenere che qualsiasi affermazione non basata sull’uno o sull’altro metodo è priva di valore.

Possiamo ricostruire l’argomento di Hume nel modo seguente. Supponiamo che t sia un qualche argomento sul quale sosteniamo di avere conoscenza. Supponiamo che non abbiamo ottenuto questa conoscenza dall’esperienza o dalla logica. Scritto in inglese, possiamo ricostruire il suo argomento nel modo seguente:

Abbiamo conoscenza su t se e solo se le nostre affermazioni su t sono apprese dal ragionamento sperimentale o dalla logica o dalla matematica.

Le nostre affermazioni su t non sono apprese dal ragionamento sperimentale.

Le nostre affermazioni su t non sono apprese dalla logica o dalla matematica.

Non abbiamo conoscenza su t.

Cosa significa questa frase “se e solo se”? I filosofi pensano che essa, e diverse frasi sinonime, siano usate spesso nei ragionamenti. Lasciando per ora inspiegabile il “se e solo”, possiamo usare la seguente chiave di traduzione per scrivere l’argomento in un mix della nostra logica proposizionale e dell’inglese.

P: Abbiamo conoscenze su t.

Q: Le nostre affermazioni su t sono apprese dal ragionamento sperimentale.

R: Le nostre affermazioni su t sono apprese dalla logica o dalla matematica.

E così abbiamo:

P se e solo se (QvR)

¬Q

¬R

¬P

Il nostro compito è di aggiungere al nostro linguaggio logico un equivalente a “se e solo se”. Poi potremo valutare questa riformulazione dell’argomento di Hume.

9.2 Il bicondizionale

Prima di introdurre un simbolo sinonimo di “se e solo se”, e poi esporre la sua sintassi e semantica, dovremmo iniziare con un’osservazione. Una frase come “P se e solo se Q” sembra essere un modo abbreviato di dire “P se Q e P solo se Q”. Una volta notato questo, non dobbiamo cercare di discernere il significato di “if and only if” usando la nostra comprensione esperta dell’inglese. Invece, possiamo discernere il significato di “se e solo se” usando le nostre già rigorose definizioni di “se”, “e” e “solo se”. In particolare, “P se Q e P solo se Q” sarà tradotto “((Q→P)^(P→Q))”. (Se questo non vi è chiaro, tornate indietro e rivedete la sezione 2.2.) Ora, facciamo una tabella di verità per questa formula.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T	T
T	F	T	F	F
F	T	F	T	F
F	F	T	T	T

Abbiamo risolto la semantica per “se e solo se”. Possiamo ora introdurre un nuovo simbolo per questa espressione. È tradizionale usare la doppia freccia, “↔”. Possiamo ora esprimere la sintassi e la semantica di “↔”.

Se Φ e Ψ sono frasi, allora

(Φ↔Ψ)

è una frase. Questo tipo di frase è tipicamente chiamato “bicondizionale”.

La semantica è data dalla seguente tabella di verità.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

Un piacevole risultato del nostro conto del bicondizionale è che ci permette di spiegare sinteticamente la nozione sintattica di equivalenza logica. Diciamo che due frasi Φ e Ψ sono “equivalenti” o “logicamente equivalenti” se (Φ↔Ψ) è un teorema.

9.3 Frasi alternative

In inglese, sembra che ci siano diverse frasi che solitamente hanno lo stesso significato del bicondizionale. Ognuna delle seguenti frasi sarebbe tradotta come (P↔Q).

P se e solo se Q.

P solo nel caso in cui Q.

P è necessario e sufficiente per Q.

P è equivalente a Q.

9.4 Ragionare con il bicondizionale

Come possiamo ragionare usando un bicondizionale? All’inizio, sembrerebbe offrire poche indicazioni. Se so che (P↔Q), so che P e Q hanno lo stesso valore di verità, ma da questa sola frase non so se sono entrambi veri o entrambi falsi. Tuttavia, possiamo approfittare della semantica del bicondizionale per osservare che se conosciamo anche il valore di verità di una delle frasi che costituiscono il bicondizionale, allora possiamo ricavare il valore di verità dell’altra frase. Questo suggerisce un semplice insieme di regole. Queste saranno in realtà quattro regole, ma le raggrupperemo sotto un unico nome, “equivalenza”:

e

e

e

E se invece stiamo cercando di mostrare un bicondizionale? Qui possiamo tornare all’intuizione che il bicondizionale (Φ↔Ψ) è equivalente a ((Φ→Ψ)^(Ψ→Φ)). Se potessimo provare sia (Φ→Ψ) che (Ψ→Φ), sapremo che (Φ↔Ψ) deve essere vero.

Possiamo chiamare questa regola “bicondizione”. Ha la seguente forma:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Questo significa che spesso, quando vogliamo provare un bicondizionale, intraprenderemo due derivazioni condizionali per ricavare due condizionali, e poi useremo la regola del bicondizionale. Cioè, molte prove di bicondizionali hanno la seguente forma:

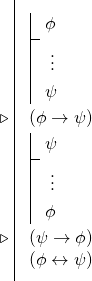
9.5 Tornando a Hume

Ora possiamo vedere se siamo in grado di provare l’argomento di Hume. Dato ora il nuovo simbolo bicondizionale, possiamo iniziare una prova diretta con le nostre tre premesse.

Abbiamo già osservato che pensiamo che (QvR) sia falso perché ¬Q e ¬R. Quindi proviamo ¬(QvR). Questa frase non può essere dimostrata direttamente, date le premesse che abbiamo; e non può essere dimostrata con una prova condizionale, poiché non è una condizionale. Proviamo allora una prova indiretta. Noi crediamo che ¬(QvR) sia vero, quindi assumiamo la negazione di questo e mostriamo una contraddizione.

L’argomento di Hume, almeno come lo abbiamo ricostruito, è valido.

L’argomento di Hume è valido? Che sia valido dipende dalla prima premessa di cui sopra (poiché la seconda e la terza premessa sono astrazioni su qualche argomento t). Più specificamente, dipende dall’affermazione che abbiamo conoscenza di qualcosa solo nel caso in cui possiamo dimostrarlo con un esperimento o con la logica. Hume sostiene che dovremmo diffidare – anzi, dovremmo bruciare i testi che contengono affermazioni che non provengono dall’esperimento e dall’osservazione, o dalla logica e dalla matematica. Ma consideriamo questa affermazione: abbiamo conoscenza su un argomento t se e solo se le nostre affermazioni su t sono apprese dall’esperimento o le nostre affermazioni su t sono apprese dalla logica o dalla matematica.

Hume ha scoperto questa affermazione attraverso gli esperimenti? O l’ha scoperta attraverso la logica? Quale destino subirebbe il libro di Hume, se seguissimo il suo consiglio?

9.6 Alcuni esempi

Può essere utile dimostrare alcuni teoremi che fanno uso del bicondizionale, per illustrare come possiamo ragionare con il bicondizionale.

Ecco un principio utile. Se due frasi hanno lo stesso valore di verità di una terza frase, allora hanno lo stesso valore di verità l’una dell’altra. Lo dichiariamo come (((P↔Q)^(R↔Q))→(P↔R)). Per illustrare il ragionamento con il bicondizionale, dimostriamo questo teorema.

Questo teorema è un condizionale, quindi richiederà una derivazione condizionale. Il conseguente del condizionale è un bicondizionale, quindi avremo bisogno di due derivazioni condizionali, una per provare (P→R) e una per provare (R→P). La prova avrà questo aspetto. Studiatela attentamente.

Abbiamo accennato prima ai principi che associamo al matematico Augustus De Morgan (1806-1871), e che oggi sono chiamati “Leggi di De Morgan” o “Equivalenze di De Morgan”. Queste sono il riconoscimento che ¬(PvQ) e (¬P^¬Q) sono equivalenti, e anche che ¬(P^Q) e (¬Pv¬Q) sono equivalenti. Possiamo ora esprimerle con il bicondizionale. I seguenti sono teoremi della nostra logica:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Proveremo il secondo di questi teoremi. Questa è forse la prova più difficile che abbiamo visto; richiede prove indirette annidate, e una buona dose di astuzia nel trovare quale sarà la contraddizione rilevante.

9.7 Uso dei teoremi

Ogni frase della nostra logica è, in termini semantici, di tre tipi. È una tautologia, una frase contraddittoria o una frase contingente. Abbiamo già definito “tautologia” (una frase che deve essere vera) e “frase contraddittoria” (una frase che deve essere falsa). Una frase contingente è una frase che non è né una tautologia né una frase contraddittoria. Così, una frase contingente è una frase che potrebbe essere vera, o potrebbe essere falsa.

Ecco un esempio di ogni tipo di frase:

(Pv¬P)

(P↔¬P)

P

La prima è una tautologia, la seconda è una frase contraddittoria, e la terza è contingente. Possiamo vedere questo con una tabella di verità.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Nota che la negazione di una tautologia è una contraddizione, la negazione di una contraddizione è una tautologia, e la negazione di una frase contingente è una frase contingente.

¬(Pv¬P)

¬(P↔¬P)

¬P

P	¬P	(Pv¬P)	¬(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	T
F	T	T	F	F	T

Un momento di riflessione rivelerà che sarebbe un vero disastro se una frase contraddittoria o una frase contingente fosse un teorema della nostra logica proposizionale. La nostra logica è stata progettata per produrre solo argomenti validi. Gli argomenti che non hanno premesse, abbiamo osservato, dovrebbero avere conclusioni che devono essere vere (di nuovo, questo segue perché una frase che può essere dimostrata senza premesse potrebbe essere dimostrata con qualsiasi premessa, e quindi dovrebbe essere vera indipendentemente dalle premesse che usiamo). Se un teorema fosse contraddittorio, sapremmo che potremmo provare una falsità. Se un teorema fosse contingente, allora a volte potremmo provare una falsità (cioè, potremmo provare una frase che è falsa a certe condizioni). E, dato che abbiamo adottato la derivazione indiretta come metodo di prova, ne consegue che una volta che abbiamo una contraddizione o una frase contraddittoria in un argomento, possiamo provare qualsiasi cosa.

I teoremi possono esserci molto utili negli argomenti. Supponiamo di sapere che né Smith né Jones andranno a Londra, e vogliamo dimostrare, quindi, che Jones non andrà a Londra. Se ci permettessimo di usare uno dei teoremi di De Morgan, potremmo fare un rapido lavoro di argomentazione. Assumiamo la seguente chiave.

P: Smith andrà a Londra.

Q: Jones andrà a Londra.

E abbiamo il seguente argomento:

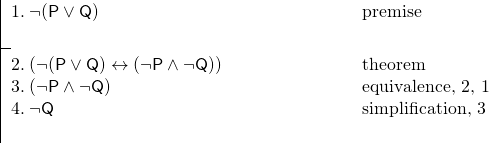
Questa dimostrazione è stata resa molto facile dal nostro uso del teorema alla linea 2.

Ci sono due cose da notare su questo. Primo, dovremmo permetterci di farlo, perché se sappiamo che una frase è un teorema, allora sappiamo che potremmo provare quel teorema in una sottoprova. Cioè, potremmo sostituire la linea 2 sopra con una lunga sottoprova che provi (¬(P v Q)↔(¬P ^ ¬Q)), che potremmo poi usare. Ma se siamo certi che (¬(P v Q)↔(¬P ^ ¬Q)) è un teorema, non dovremmo avere bisogno di rifare questa prova ogni volta che vogliamo fare uso del teorema.

Il secondo problema che dobbiamo riconoscere è più sottile. Ci sono infinite frasi della forma del nostro teorema, e dovremmo essere in grado di usare anche quelle. Per esempio, le seguenti frasi avrebbero ciascuna una prova identica alla nostra prova del teorema (¬(P v Q)↔(¬P ^ ¬Q)), tranne che le lettere sarebbero diverse:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Questo è spero ovvio. Prendete la prova di (¬(P v Q)↔(¬P ^ ¬Q)), e in quella prova sostituite ogni istanza di P con R e ogni istanza di Q con S, e avrete una prova di (¬(R v S)↔(¬R ^ ¬S)).

Ma ecco qualcosa che forse è meno ovvio. Ognuno dei seguenti può essere pensato come simile al teorema (¬(P v Q)↔(¬P ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ¬(R^S)))

(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(R→¬Q)))

Ad esempio, se si prendesse una dimostrazione di (¬(P v Q)↔(¬P ^ ¬Q)) e si sostituisse ogni istanza iniziale di P con (Q↔P) e ogni istanza iniziale di Q con (¬R→¬Q), allora si avrebbe una dimostrazione del teorema (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q))).

Si potrebbe cogliere questa intuizione in due modi. Potremmo enunciare teoremi del nostro metalinguaggio e permettere che questi abbiano istanze. Così, potremmo prendere (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) come un teorema del metalinguaggio, in cui potremmo sostituire ogni Φ con una frase e ogni Ψ con una frase e ottenere una particolare istanza di un teorema. Un’alternativa è permettere che da un teorema si possano produrre altri teoremi attraverso la sostituzione. Per comodità, adotteremo questa seconda strategia.

La nostra regola sarà questa. Una volta dimostrato un teorema, possiamo citarlo in una dimostrazione in qualsiasi momento. La nostra giustificazione è che l’affermazione è un teorema. Permettiamo la sostituzione di qualsiasi frase atomica nel teorema con qualsiasi altra frase se e solo se sostituiamo ogni istanza iniziale di quella frase atomica nel teorema con la stessa frase.

Prima di considerare un esempio, è utile elencare alcuni teoremi utili. Ci sono infiniti teoremi del nostro linguaggio, ma questi dieci sono spesso molto utili. Alcuni li abbiamo dimostrati. Gli altri possono essere dimostrati come esercizio.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Alcuni esempi renderanno chiaro il vantaggio di usare i teoremi. Consideriamo un argomento diverso, basato su quello precedente. Sappiamo che non è vero che se Smith va a Londra, andrà a Berlino, né che se Jones va a Londra andrà a Berlino. Vogliamo dimostrare che non è il caso che Jones vada a Berlino. Aggiungiamo alla nostra chiave quanto segue:

R: Smith andrà a Berlino.

S: Jones andrà a Berlino.

E abbiamo il seguente argomento:

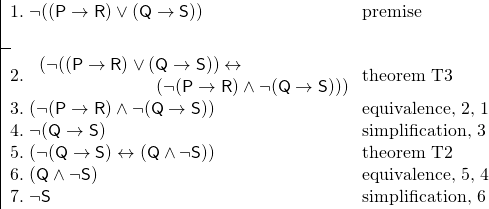
L’uso dei teoremi ha reso questa prova molto più breve di quanto sarebbe stata altrimenti. Inoltre, i teoremi spesso rendono una dimostrazione più facile da seguire, poiché riconosciamo i teoremi come tautologie, come frasi che devono essere vere.

9.8 Problemi

1. Provare che ciascuno dei seguenti argomenti è valido.

1. Premesse: P, ¬Q. Conclusione: ¬(P↔Q).
2. Premesse: (¬PvQ), (Pv¬Q). Conclusione: (P↔Q).
3. Premesse: (P↔Q), (R↔S) . Conclusione: ((P^R)↔(Q^S)).

1. Provare ciascuno dei seguenti teoremi.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. T9
9. ((P^Q)↔¬(¬Pv¬Q))
10. ((P→Q)↔¬(P^¬Q))

1. In un normale inglese colloquiale, scrivete la vostra argomentazione valida con almeno due premesse, di cui almeno una è un bicondizionale. La vostra argomentazione dovrebbe essere solo un paragrafo (non una lista ordinata di frasi o qualsiasi altra cosa che assomigli alla logica formale). Traducilo in logica proposizionale e dimostra che è valido.
2. In inglese colloquiale normale, scrivi il tuo argomento valido con almeno due premesse, e con una conclusione che sia un bicondizionale. Il tuo argomento dovrebbe essere solo un paragrafo (non una lista ordinata di frasi o qualsiasi altra cosa che assomigli alla logica formale). Traducilo in logica proposizionale e dimostra che è valido.