Une introduction concise à la logique

9.1 Un exemple historique

On se souvient du philosophe David Hume (1711-1776) comme d’un brillant empiriste sceptique. Une personne est sceptique sur un sujet si elle a à la fois des normes très strictes pour ce qui constitue la connaissance sur ce sujet et croit également que nous ne pouvons pas répondre à ces normes strictes. L’empirisme est le point de vue selon lequel nous acquérons des connaissances principalement par l’expérience, en particulier l’expérience de nos sens. Dans son livre, An Inquiry Concerning Human Understanding, Hume énonce ses principes de connaissance, puis nous conseille de nettoyer nos bibliothèques :

Quand nous courons sur les bibliothèques, persuadés de ces principes, quel ravage devons-nous faire ? Si nous prenons en main un volume quelconque de divinité ou de métaphysique scolaire, par exemple, demandons-nous : contient-il un raisonnement abstrait sur la quantité ou le nombre ? Non. Contient-il un raisonnement expérimental sur les faits et l’existence ? Non. Livrez-le alors aux flammes, car il ne peut contenir que des sophismes et des illusions.

Hume estimait que les seules sources de connaissance étaient le raisonnement logique ou mathématique (qu’il appelle ci-dessus « raisonnement abstrait concernant la quantité ou le nombre ») ou l’expérience des sens (« raisonnement expérimental concernant la matière du fait et de l’existence »). Hume est amené à soutenir que toute affirmation qui ne repose pas sur l’une ou l’autre méthode est sans valeur.

Nous pouvons reconstruire l’argument de Hume de la manière suivante. Supposons que t soit un sujet sur lequel nous prétendons avoir une connaissance. Supposons que nous n’ayons pas obtenu cette connaissance par l’expérience ou la logique. Rédigé en anglais, nous pouvons reconstruire son argument de la manière suivante :

Nous avons une connaissance sur t si et seulement si nos affirmations sur t sont apprises par un raisonnement expérimental ou par la logique ou les mathématiques.

Nos affirmations sur t ne sont pas apprises du raisonnement expérimental.

Nos affirmations sur t ne sont pas apprises de la logique ou des mathématiques.

Nous n’avons pas de connaissance sur t.

Que signifie cette expression « si et seulement si » ? Les philosophes pensent qu’elle, ainsi que plusieurs phrases synonymes, sont souvent utilisées dans les raisonnements. En laissant « si et seulement » inexpliqué pour le moment, nous pouvons utiliser la clé de traduction suivante pour écrire l’argument dans un mélange de notre logique propositionnelle et de l’anglais.

P : Nous avons des connaissances sur t.

Q : Nos affirmations sur t sont apprises par un raisonnement expérimental.

R : Nos affirmations sur t sont apprises de la logique ou des mathématiques.

Et donc nous avons:

P si et seulement si (QvR)

¬Q

¬R

¬P

Notre tâche est d’ajouter à notre langage logique un équivalent à « si et seulement si ». Nous pourrons alors évaluer cette reformulation de l’argument de Hume.

9.2 Le biconditionnel

Avant d’introduire un symbole synonyme de « si et seulement si », puis d’en exposer la syntaxe et la sémantique, nous devons commencer par une observation. Une phrase comme « P si et seulement si Q » semble être une manière abrégée de dire « P si Q et P seulement si Q ». Une fois que nous l’avons remarqué, nous n’avons pas besoin d’essayer de discerner le sens de « if and only if » en utilisant notre compréhension experte de l’anglais. Au lieu de cela, nous pouvons discerner le sens de « si et seulement si » en utilisant nos définitions déjà rigoureuses de « si », « et », et « seulement si ». Plus précisément, « P si Q et P seulement si Q » sera traduit par « ((Q→P)^(P→Q)) ». (Si cela n’est pas clair pour vous, revenez en arrière et revoyez la section 2.2.) Maintenant, faisons une table de vérité pour cette formule.

.

.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T
T	F	T	F	F
F	T	F	T	F
F	F	T	T	T

Nous avons réglé la sémantique de « si et seulement si ». Nous pouvons maintenant introduire un nouveau symbole pour cette expression. Il est traditionnel d’utiliser la double flèche, « ↔ ». Nous pouvons maintenant exprimer la syntaxe et la sémantique de « ↔ ».

Si Φ et Ψ sont des phrases, alors

(Φ↔Ψ)

est une phrase. Ce type de phrase est typiquement appelé « biconditionnel ».

La sémantique est donnée par la table de vérité suivante.

.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

Un résultat agréable de notre compte du biconditionnel est qu’il nous permet d’expliquer succinctement la notion syntaxique d’équivalence logique. Nous disons que deux phrases Φ et Ψ sont « équivalentes » ou « logiquement équivalentes » si (Φ↔Ψ) est un théorème.

9.3 Phrases alternatives

En anglais, il semble qu’il existe plusieurs phrases qui ont généralement le même sens que le biconditionnel. Chacune des phrases suivantes se traduirait par (P↔Q).

P if and only if Q.

P just in case Q.

P is necessary and sufficient for Q.

P is equivalent to Q.

9.4 Reasoning with the biconditional

Comment peut-on raisonner en utilisant un biconditionnel ? Au premier abord, il semblerait qu’il offre peu d’indications. Si je sais que (P↔Q), je sais que P et Q ont la même valeur de vérité, mais à partir de cette seule phrase, je ne sais pas s’ils sont tous deux vrais ou tous deux faux. Néanmoins, nous pouvons profiter de la sémantique du biconditionnel pour observer que si nous connaissons également la valeur de vérité d’une des phrases constituant le biconditionnel, alors nous pouvons déduire la valeur de vérité de l’autre phrase. Cela suggère un ensemble de règles simples. Il s’agira en fait de quatre règles, mais nous les regrouperons sous un seul nom, « équivalence » :

et

et

et

Qu’en est-il si nous essayons plutôt de montrer un biconditionnel ? Ici, nous pouvons revenir à l’intuition que le biconditionnel (Φ↔Ψ) est équivalent à ((Φ→Ψ)^(Ψ→Φ)). Si nous pouvions prouver à la fois (Φ→Ψ) et (Ψ→Φ), nous saurons que (Φ↔Ψ) doit être vrai.

Nous pouvons appeler cette règle « bicondition ». Elle a la forme suivante:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Cela signifie que souvent, lorsque nous visons à prouver une bicondition, nous entreprendrons deux dérivations conditionnelles pour dériver deux conditionnels, puis nous utiliserons la règle de bicondition. C’est-à-dire que de nombreuses preuves de biconditionnelles ont la forme suivante :

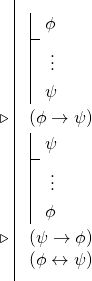
9.5 Retour à Hume

Nous pouvons maintenant voir si nous sommes capables de prouver l’argument de Hume. Étant donné maintenant le nouveau symbole biconditionnel, nous pouvons commencer une preuve directe avec nos trois prémisses.

Nous avons déjà observé que nous pensons que (QvR) est faux parce que ¬Q et ¬R. Prouvons donc ¬(QvR). Cette phrase ne peut pas être prouvée directement, étant donné les prémisses que nous avons ; et elle ne peut pas être prouvée avec une preuve conditionnelle, puisqu’elle n’est pas un conditionnel. Essayons donc une preuve indirecte. Nous croyons que ¬(QvR) est vrai, donc nous allons supposer la négation de ceci et montrer une contradiction.

L’argument de Hume, au moins tel que nous l’avons reconstruit, est valide.

L’argument de Hume est-il solide ? La question de savoir s’il est solide dépend de la première prémisse ci-dessus (puisque les deuxième et troisième prémisses sont des abstractions sur un certain sujet t). Plus précisément, il dépend de l’affirmation selon laquelle nous avons la connaissance de quelque chose juste au cas où nous pouvons le montrer par l’expérience ou la logique. Hume soutient que nous devrions nous méfier – en fait, nous devrions brûler les textes contenant – des affirmations qui ne sont pas issues de l’expérience et de l’observation, ou de la logique et des mathématiques. Mais considérez cette affirmation : nous avons une connaissance sur un sujet t si et seulement si nos affirmations sur t sont apprises par l’expérience ou si nos affirmations sur t sont apprises par la logique ou les mathématiques.

Hume a-t-il découvert cette affirmation par des expériences ? Ou l’a-t-il découverte par la logique ? Quel sort subirait le livre de Hume, si nous suivions son conseil ?

9.6 Quelques exemples

Il peut être utile de prouver quelques théorèmes qui font usage du biconditionnel, afin d’illustrer comment nous pouvons raisonner avec le biconditionnel.

Voici un principe utile. Si deux phrases ont la même valeur de vérité qu’une troisième phrase, alors elles ont la même valeur de vérité l’une que l’autre. On l’énonce sous la forme (((P↔Q)^(R↔Q))→(P↔R)). Pour illustrer le raisonnement avec le biconditionnel, prouvons ce théorème.

Ce théorème est un conditionnel, il nécessitera donc une dérivation conditionnelle. Le conséquent du conditionnel est un biconditionnel, donc nous nous attendrons à avoir besoin de deux dérivations conditionnelles, une pour prouver (P→R) et une pour prouver (R→P). La preuve ressemblera à ceci . Étudiez-la de près.

Nous avons mentionné auparavant les principes que nous associons au mathématicien Augustus De Morgan (1806-1871), et que l’on appelle aujourd’hui « les lois de De Morgan » ou les « équivalences de De Morgan ». Il s’agit de la reconnaissance que ¬(PvQ) et (¬P^¬Q) sont équivalents, et aussi que ¬(P^Q) et (¬Pv¬Q) sont équivalents. Nous pouvons maintenant les exprimer avec le biconditionnel. Voici les théorèmes de notre logique :

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Nous allons prouver le deuxième de ces théorèmes. C’est peut-être la preuve la plus difficile que nous ayons vue ; elle nécessite des preuves indirectes imbriquées, et une bonne dose d’ingéniosité pour trouver quelle sera la contradiction pertinente.

9.7 Utilisation des théorèmes

Chaque phrase de notre logique est, en termes sémantiques, de trois sortes. C’est soit une tautologie, soit une phrase contradictoire, soit une phrase contingente. Nous avons déjà défini « tautologie » (une phrase qui doit être vraie) et « phrase contradictoire » (une phrase qui doit être fausse). Une phrase contingente est une phrase qui n’est ni une tautologie ni une phrase contradictoire. Ainsi, une phrase contingente est une phrase qui pourrait être vraie, ou qui pourrait être fausse.

Voici un exemple de chaque type de phrase:

(Pv¬P)

(P↔¬P)

P

La première est une tautologie, la deuxième est une phrase contradictoire, et la troisième est contingente. On peut voir cela avec une table de vérité.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Notez que la négation d’une tautologie est une contradiction, la négation d’une contradiction est une tautologie, et la négation d’une phrase contingente est une phrase contingente.

¬(Pv¬P)

¬(P↔¬P)

¬P

.

P	¬P	(Pv¬P)	¬(Pv¬P)	(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	T
F	T	T	F	F	T

Un moment de réflexion révélera que ce serait un véritable désastre si une phrase contradictoire ou une phrase contingente était un théorème de notre logique propositionnelle. Notre logique a été conçue pour ne produire que des arguments valides. Les arguments qui n’ont pas de prémisses, avons-nous observé, devraient avoir des conclusions qui doivent être vraies (encore une fois, cela découle du fait qu’une phrase qui peut être prouvée sans prémisses pourrait être prouvée avec n’importe quelles prémisses, et donc elle a intérêt à être vraie, peu importe les prémisses que nous utilisons). Si un théorème était contradictoire, nous saurions que nous pouvons prouver une fausseté. Si un théorème était contingent, alors nous pourrions parfois prouver une fausseté (c’est-à-dire que nous pourrions prouver une phrase qui est fausse sous certaines conditions). Et, étant donné que nous avons adopté la dérivation indirecte comme méthode de preuve, il s’ensuit qu’une fois que nous avons une contradiction ou une phrase contradictoire dans un argument, nous pouvons prouver n’importe quoi.

Les théorèmes peuvent nous être très utiles dans les arguments. Supposons que nous savons que ni Smith ni Jones n’iront à Londres, et que nous voulons prouver, par conséquent, que Jones n’ira pas à Londres. Si nous nous permettons d’utiliser l’un des théorèmes de De Morgan, nous pourrions faire un travail rapide sur l’argument. Supposons la clé suivante.

P : Smith ira à Londres.

Q : Jones ira à Londres.

Et nous avons l’argument suivant:

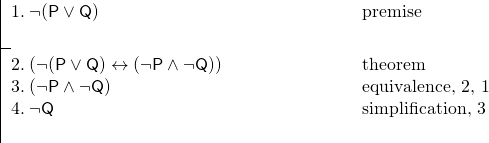
Cette preuve a été rendue très facile par notre utilisation du théorème à la ligne 2.

Il y a deux choses à noter à ce sujet. Premièrement, nous devrions nous permettre de le faire, car si nous savons qu’une phrase est un théorème, alors nous savons que nous pourrions prouver ce théorème dans une sous-preuve. C’est-à-dire que nous pourrions remplacer la ligne 2 ci-dessus par une longue sous-épreuve qui prouve (¬(P v Q)↔(¬P ^ ¬Q)), que nous pourrions alors utiliser. Mais si nous sommes certains que (¬(P v Q)↔(¬P ^ ¬Q)) est un théorème, nous ne devrions pas avoir besoin de faire cette preuve encore et encore, chaque fois que nous voulons faire usage du théorème.

Le deuxième problème que nous devrions reconnaître est plus subtil. Il existe une infinité de phrases de la forme de notre théorème, et nous devrions être en mesure de les utiliser également. Par exemple, les phrases suivantes auraient chacune une preuve identique à notre preuve du théorème (¬(P v Q)↔(¬P ^ ¬Q)), sauf que les lettres seraient différentes :

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

On espère que c’est évident. Prenez la preuve de (¬(P v Q)↔(¬P ^ ¬Q)), et dans cette preuve remplacez chaque instance de P par R et chaque instance de Q par S, et vous auriez une preuve de (¬(R v S)↔(¬R ^ ¬S)).

Mais voici quelque chose qui est peut-être moins évident. Chacun des éléments suivants peut être considéré comme similaire au théorème (¬(P v Q)↔(¬P ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))

Par exemple, si on prenait une preuve de (¬(P v Q)↔(¬P ^ ¬Q)) et qu’on remplaçait chaque instance initiale de P par (Q↔P) et chaque instance initiale de Q par (¬R→¬Q), alors on aurait une preuve du théorème (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)))).

Nous pourrions capturer cette intuition de deux manières. Nous pourrions énoncer des théorèmes de notre métalangage et permettre que ceux-ci aient des instances. Ainsi, nous pourrions prendre (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) comme un théorème du métalangage, dans lequel nous pourrions remplacer chaque Φ par une phrase et chaque Ψ par une phrase et obtenir une instance particulière d’un théorème. Une alternative est de permettre qu’à partir d’un théorème nous puissions produire d’autres théorèmes par substitution. Par facilité, nous prendrons cette deuxième stratégie.

Notre règle sera la suivante . Une fois que nous avons prouvé un théorème, nous pouvons le citer dans une preuve à tout moment. Notre justification est que la preuve est un théorème. Nous permettons la substitution de toute phrase atomique dans le théorème par toute autre phrase si et seulement si nous remplaçons chaque instance initiale de cette phrase atomique dans le théorème par la même phrase.

Avant de considérer un exemple, il est bénéfique d’énumérer quelques théorèmes utiles. Il existe une infinité de théorèmes de notre langue, mais ces dix-là sont souvent très utiles. Nous en avons prouvé quelques-uns. Les autres peuvent être prouvés comme un exercice.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Certains exemples rendront clair l’avantage d’utiliser des théorèmes. Considérons un argument différent, s’appuyant sur celui qui précède. Nous savons que ce n’est pas le cas que si Smith va à Londres, il ira à Berlin, ni le cas que si Jones va à Londres, il ira à Berlin. Nous voulons prouver que ce n’est pas le cas que Jones aille à Berlin. Nous ajoutons ce qui suit à notre clé:

R : Smith ira à Berlin.

S : Jones ira à Berlin.

Et nous avons l’argument suivant:

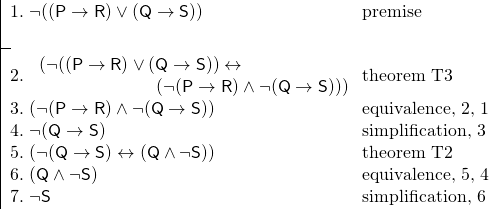
L’utilisation de théorèmes a rendu cette preuve beaucoup plus courte qu’elle ne l’aurait été autrement. De plus, les théorèmes rendent souvent une preuve plus facile à suivre, puisque nous reconnaissons les théorèmes comme des tautologies – comme des phrases qui doivent être vraies.

9.8 Problèmes

1. Prouvez que chacun des arguments suivants est valide.

1. Prémisses : P, ¬Q. Conclusion : ¬(P↔Q).
2. Prémisses : (¬PvQ), (Pv¬Q). Conclusion : (P↔Q).
3. Prémisses : (P↔Q), (R↔S) . Conclusion : ((P^R)↔(Q^S)).

1. Protester chacun des théorèmes suivants.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q))
9. ((P→Q)↔¬(P^¬Q))

1. En anglais familier normal, écrivez votre propre argument valide avec au moins deux prémisses, dont au moins une est un biconditionnel. Votre argument doit juste être un paragraphe (pas une liste ordonnée de phrases ou autre chose qui ressemble à de la logique formelle). Traduisez-le en logique propositionnelle et prouvez qu’il est valide.
2. En anglais familier normal, écrivez votre propre argument valide avec au moins deux prémisses, et avec une conclusion qui est une biconditionnelle. Votre argument devrait juste être un paragraphe (pas une liste ordonnée de phrases ou quoi que ce soit d’autre qui ressemble à de la logique formelle). Traduisez-le en logique propositionnelle et prouvez qu’il est valide.