Dans cette leçon, nous allons montrer une stratégie facile pour résoudre le problème suivant : comment trouver l’aire d’un triangle isocèle.
Mettons en pratique un certain nombre des propriétés que nous avons prouvées jusqu’à présent, dans le problème de géométrie suivant :
Problème
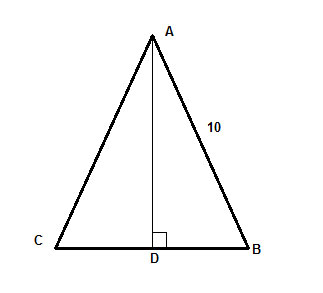
Dans un triangle isocèle, ΔABC, de longueur de jambe 10, la hauteur à la base est égale aux deux tiers de la base. Trouvez l’aire du triangle.
Stratégie
Pour résoudre ce problème, Nous allons travailler à rebours de ce que nous devons faire.
Nous devons trouver l’aire du triangle qui, nous le savons, est donnée par la formule (base fois hauteur)/2.
Un problème que nous avons est que nous ne connaissons ni la longueur de la base ni la hauteur. Mais, on nous donne la relation entre elles, ce qui est l’indice de ce que nous devons faire. Appelons la longueur de la base, BC, x.
Puis nous savons que la hauteur, AD, est 2x/3, comme indiqué dans le problème.
Donc la réponse que nous cherchons est (base fois hauteur)/2, ou x fois 2x/3, divisé par deux.
Mais comment trouver x ? Il y a deux choses supplémentaires qui nous ont été données dans le problème et que nous n’avons pas encore utilisées – la longueur de la jambe (10), et le fait que c’est un triangle isocèle. Nous devons probablement utiliser ces deux choses pour résoudre le problème.
Revoyons les propriétés des triangles isocèles. Une chose qui devrait immédiatement sauter aux yeux est que, comme nous l’avons montré, dans un triangle isocèle, la hauteur à la base coupe la base en deux, donc CD=DB=x/2.
Enfin, AD est la hauteur, ce qui signifie que l’angle ∠ADC est un angle droit, et nous avons un triangle rectangle, ΔADC, dont nous connaissons l’hypoténuse (10) et pouvons utiliser pour trouver les jambes en utilisant le théorème de Pythagore, c2 =a2+b2,
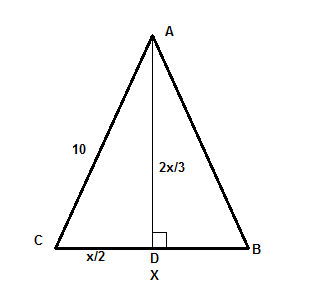
où c= 10 ,a = x/2 et b=2x/3 . Et nous avons terminé, le reste n’est que la résolution algébrique de x.
Preuve : Aire d’un triangle isocèle
(1) ΔADC est un triangle rectangle //donné, car AD est la hauteur à la base
(2) AC2 =CD2 + AD2 /Théorème de Pythagore
(3) AC= 10 //donné
(4) CB = x
(5) CD = x/2 /La hauteur à la base dans un triangle isocèle coupe la base en deux
(6) AD = 2x/3 //donné
(7) 102 = (x/2)2 + (2x/3)2 //Substituer dans (2)
(8) 100 = x2/4+4×2/9 //simplifier
(9) 100*36 = 9×2 +16×2 //multiplier les deux côtés par 36
(10) 100*36 = 25×2 //collecter les termes similaires
.