Réponse 7 – 7 – 7 = 73 On lit « sept cubes ».

Comprendre les exposants et les racines carrées

Objectif(s) d’apprentissage :

– Évaluer des expressions contenant des exposants.

– Écrire des facteurs répétés en utilisant la notation exponentielle.

– Trouver une racine carrée d’un carré parfait.

Les exposants fournissent une façon spéciale d’écrire une multiplication répétée. Les nombres écrits de cette façon ont une forme spécifique, chaque partie fournissant des informations importantes sur le nombre. L’écriture des nombres à l’aide d’exposants permet également de gagner beaucoup de place. L’opération inverse de la multiplication d’un nombre par lui-même s’appelle trouver la racine carrée d’un nombre. Cette opération est utile pour les problèmes concernant l’aire d’un carré.

La notation exponentielle est une façon spéciale d’écrire les facteurs répétés, par exemple 7 – 7. La notation exponentielle comporte deux parties. Une partie de la notation est appelée la base. La base est le nombre qui est multiplié par lui-même. L’autre partie de la notation est l’exposant, ou puissance. Il s’agit du petit nombre écrit en haut à droite de la base. L’exposant, ou puissance, indique combien de fois la base doit être utilisée comme facteur dans la multiplication. Dans l’exemple, 7 – 7 peut s’écrire 72, 7 étant la base et 2 l’exposant. L’exposant 2 signifie qu’il y a deux facteurs.

72 = 7 – 7 = 49

Vous pouvez lire 72 comme « sept au carré ». En effet, multiplier un nombre par lui-même s’appelle « élever un nombre au carré ». De même, élever un nombre à une puissance de 3 s’appelle « cuber le nombre ». Vous pouvez lire 73 comme « sept au cube ».

Vous pouvez lire 25 comme « deux à la cinquième puissance » ou « deux à la puissance de cinq ». Vous pouvez lire 84 comme « huit à la quatrième puissance » ou « huit à la puissance quatre ». Ce format peut être utilisé pour lire n’importe quel nombre écrit en notation exponentielle. En fait, si 63 se lit le plus souvent « six cubes », il peut aussi être lu « six à la troisième puissance » ou « six à la puissance trois. »

Pour trouver la valeur d’un nombre écrit sous forme exponentielle, réécrivez le nombre comme une multiplication répétée et effectuez la multiplication. Deux exemples sont présentés ci-dessous.

Trouver la valeur de 43.

A) 12

B) 64

C) 256

D) 43

Écrire une multiplication répétée en notation exponentielle peut faire gagner du temps et de l’espace. Considérons l’exemple 5 – 5 – 5 – 5 – 5. Nous pouvons utiliser la notation exponentielle pour écrire cette multiplication répétée sous la forme 54. Puisque 5 est multiplié, il est écrit comme base. Puisque la base est utilisée 4 fois dans la multiplication, l’exposant est 4. L’expression 5 – 5 – 5 – 5 peut être réécrite en notation exponentielle abrégée sous la forme 54 et se lit, « cinq à la quatrième puissance » ou « cinq à la puissance de 4. »

Pour écrire la multiplication répétée d’un même nombre en notation exponentielle, écrivez d’abord le nombre qui est multiplié comme base. Puis comptez combien de fois ce nombre est utilisé dans la multiplication, et écrivez ce nombre comme l’exposant. Assurez-vous de compter les nombres, et non les signes de multiplication, pour déterminer l’exposant.

Ecrire 10 – 10 – 10 – 10 – 10 – 10 – 10 en notation exponentielle.

A) 1.000.000

B) 60

C) 105

D) 106

Comme vous l’avez vu précédemment, 52 est appelé « cinq au carré ». « Cinq au carré » signifie multiplier cinq par lui-même. En mathématiques, on appelle multiplier un nombre par lui-même « élever au carré » le nombre. Le résultat de l’élévation au carré d’un nombre entier est appelé un carré ou un carré parfait. Un carré parfait est un nombre qui peut être écrit comme un nombre entier élevé à la puissance 2. Par exemple, 9 est un carré parfait. Un nombre carré parfait peut être représenté par une forme carrée, comme indiqué ci-dessous. Nous voyons que 1, 4, 9, 16, 25 et 36 sont des exemples de carrés parfaits.

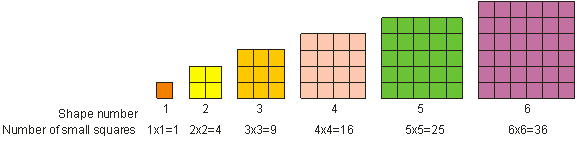
Pour élever un nombre au carré, il faut le multiplier par lui-même. 3 au carré = 32 = 3 – 3 = 9.

Vous trouverez ci-dessous d’autres exemples de carrés parfaits.

L’opération inverse d’élever un nombre au carré s’appelle trouver la racine carrée d’un nombre. Trouver une racine carrée revient à se demander « quel nombre multiplié par lui-même me donnera ce nombre ? ». La racine carrée de 25 est 5, car 5 multiplié par lui-même est égal à 25. Les racines carrées s’écrivent avec le symbole mathématique, appelé signe radical, qui ressemble à ceci : . La « racine carrée de 25 » s’écrit .

Trouver .

A) 6

B) 18

C) 72

D) 7

La notation exponentielle est une façon abrégée d’écrire la multiplication répétée d’un même nombre. Un nombre écrit en notation exponentielle a une base et un exposant, et chacune de ces parties fournit des informations pour trouver la valeur de l’expression. La base indique le nombre qui est multiplié de manière répétée, et l’exposant indique combien de fois la base est utilisée dans la multiplication. Les exposants 2 et 3 ont des noms spéciaux. Elever une base à une puissance de 2 s’appelle « élever au carré » un nombre. Augmenter une base à une puissance de 3 s’appelle « cuber » un nombre. L’inverse de l’élévation au carré d’un nombre est la recherche de la racine carrée d’un nombre. Pour trouver la racine carrée d’un nombre, demandez-vous :  » Quel nombre puis-je multiplier par lui-même pour obtenir ce nombre ? « 

.