Un satellite est un corps qui se déplace autour d’un autre corps selon une trajectoire mathématiquement prévisible appelée orbite. Un satellite de communication n’est rien d’autre qu’une station répétitrice de micro-ondes dans l’espace qui est utile dans les télécommunications, la radio et la télévision ainsi que les applications Internet.
Un répétiteur est un circuit qui augmente la force du signal qu’il reçoit et le retransmet. Mais ici, ce répéteur fonctionne comme un transpondeur, qui change la bande de fréquence du signal émis, par rapport à celle reçue.
La fréquence avec laquelle le signal est envoyé dans l’espace est appelée fréquence de liaison montante, tandis que la fréquence avec laquelle il est envoyé par le transpondeur est la fréquence de liaison descendante.
La figure suivante illustre clairement ce concept.
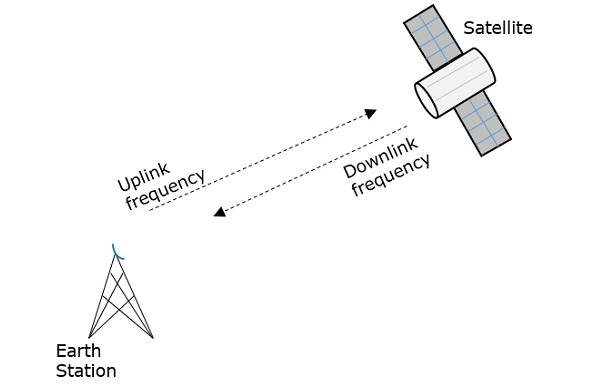
Maintenant, voyons les avantages, les inconvénients et les applications des communications par satellite.
Communication par satellite – Avantages
Les communications par satellite présentent de nombreux avantages tels que –
-
Flexibilité
-
Facilité d’installation de nouveaux circuits
-
Les distances sont facilement couvertes et le coût n’a pas d’importance
-
Diffusion. possibilités
-
Chaque coin de la terre est couvert
-
L’utilisateur peut contrôler le réseau
Communication par satellite – Inconvénients
La communication par satellite présente les inconvénients suivants –
-
Les coûts initiaux tels que les coûts de segment et de lancement sont trop élevés.
-
Congestion des fréquences
-
Interférences et propagation
Communication par satellite – Applications
La communication par satellite trouve ses applications dans les domaines suivants –
-
En radiodiffusion.
-
Dans la diffusion télévisuelle telle que le DTH.
-
Dans les applications Internet telles que la fourniture d’une connexion Internet pour le transfert de données, les applications GPS, la navigation sur Internet, etc.
-
Pour les communications vocales.
-
Pour le secteur de la recherche et du développement, dans de nombreux domaines.
-
Dans les applications militaires et les navigations.
L’orientation du satellite sur son orbite dépend des trois lois appelées lois de Kepler.
Les lois de Kepler
Johannes Kepler (1571-1630) le scientifique astronomique, a donné 3 lois révolutionnaires, concernant le mouvement des satellites. La trajectoire suivie par un satellite autour de son primaire (la terre) est une ellipse. L’ellipse a deux foyers – F1 et F2, la terre étant l’un d’eux.
Si l’on considère la distance du centre de l’objet à un point de sa trajectoire elliptique, alors le point le plus éloigné d’une ellipse du centre est appelé apogée et le point le plus court d’une ellipse du centre est appelé périgée.
La 1ère loi de Kepler
La 1ère loi de Kepler stipule que, « chaque planète tourne autour du soleil sur une orbite elliptique, avec le soleil comme un de ses foyers. » Ainsi, un satellite se déplace dans une trajectoire elliptique avec la terre comme l’un de ses foyers.
Le semi grand axe de l’ellipse est noté ‘a’ et le semi petit axe est noté ‘b’. Par conséquent, l’excentricité e de ce système peut être écrite comme –
$$e = \frac{\sqrt{a^{2}-b^{2}}{a}$
-
Excentricité (e) – C’est le paramètre qui définit la différence de forme de l’ellipse plutôt que celle d’un cercle.
-
Semi grand axe (a) – C’est le plus long diamètre tracé joignant les deux foyers le long du centre, qui touche les deux apogées (points les plus éloignés d’une ellipse du centre).
-
Axe semi-minor (b) – C’est le plus court diamètre tracé à travers le centre qui touche les deux périgées (points les plus courts d’une ellipse à partir du centre).
Ceux-ci sont bien décrits dans la figure suivante.
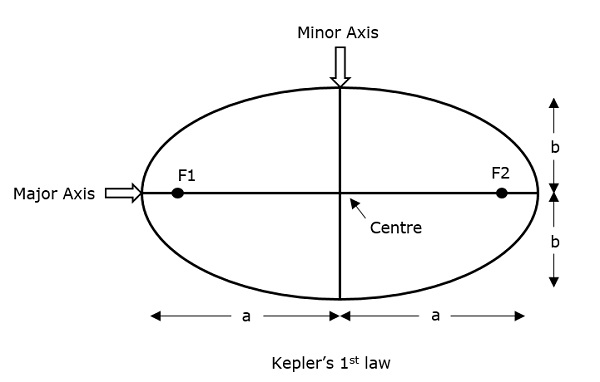
Pour une trajectoire elliptique, il est toujours souhaitable que l’excentricité se situe entre 0 et 1, c’est-à-dire.c’est-à-dire 0 < e < 1 car si e devient nul, le chemin ne sera plus en forme elliptique plutôt il sera converti en un chemin circulaire.
La 2e loi de Kepler
La 2e loi de Kepler stipule que, « pour des intervalles de temps égaux, la surface couverte par le satellite est égale par rapport au centre de la terre. »
On peut le comprendre en jetant un coup d’œil à la figure suivante.
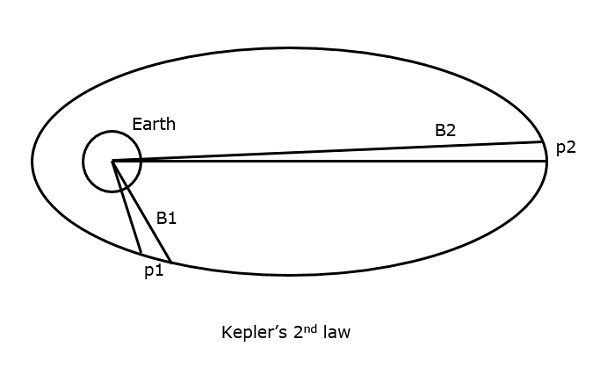
Supposons que le satellite parcourt p1 et p2 distances, dans le même intervalle de temps, alors les aires B1 et B2 parcourues respectivement dans les deux cas, sont égales.
Troisième loi de Kepler
La troisième loi de Kepler stipule que « Le carré du temps périodique de l’orbite est proportionnel au cube de la distance moyenne entre les deux corps. »
Cela peut s’écrire mathématiquement comme
$$T^{2}\:\alpha\:\ :a^{3}$
Ce qui implique
$T^{2} = \frac{4\pi ^{2}}{GM}a^{3}$
Où $^frac{4\pi ^{2}{GM}$ est la constante de proportionnalité (selon la mécanique newtonienne)
$T^{2} = \frac{4\pi ^{2}}{\mu}a^{3}$
Où μ = la constante gravitationnelle géocentrique de la terre, i.c’est-à-dire Μ = 3.986005 × 1014 m3/sec2
$$1 = \left ( \frac{2\pi}{T} \right )^{2}\frac{a^{3}}{\mu}$
$1 = n^{2}\frac{a^{3}{\mu}\:\:\:\:\:\:\:\:\:\ :a^{3} = \frac{\mu}{n^{2}}$
Où n = le mouvement moyen du satellite en radians par seconde
Le fonctionnement orbital des satellites est calculé à l’aide de ces lois de Kepler.
A côté de celles-ci, il y a une chose importante qui doit être notée. Un satellite, lorsqu’il tourne autour de la terre, subit une force de traction de la terre qui est la force gravitationnelle. Il subit également une certaine force d’attraction de la part du soleil et de la lune. Il y a donc deux forces qui agissent sur lui. Elles sont –
-
Force centripète – La force qui tend à attirer un objet se déplaçant sur une trajectoire, vers lui-même est appelée force centripète.
-
Force centrifuge – La force qui tend à pousser un objet se déplaçant sur une trajectoire, loin de sa position est appelée force centrifuge.
Donc, un satellite doit équilibrer ces deux forces pour se maintenir dans son orbite.
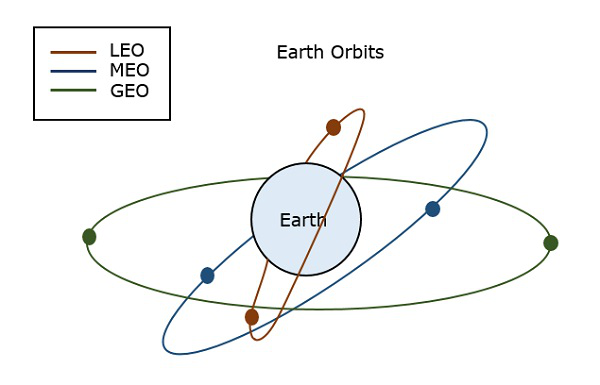
Orbites terrestres
Un satellite, lorsqu’il est lancé dans l’espace, doit être placé sur une certaine orbite afin de fournir une voie particulière pour sa révolution, de manière à maintenir l’accessibilité et à servir son objectif qu’il soit scientifique, militaire ou commercial. Les orbites attribuées aux satellites par rapport à la Terre sont appelées orbites terrestres. Les satellites qui se trouvent sur ces orbites sont des satellites à orbite terrestre.
Les types importants d’orbites terrestres sont –
-
Orbite terrestre géosynchrone
-
Orbite terrestre moyenne
-
Orbite terrestre basse
Satellites à orbite terrestre géosynchrone
Une orbite terrestre géosynchrone (GE).Synchronous Earth Orbit (GEO) est un satellite qui est placé à une altitude de 22,300 miles au-dessus de la Terre. Cette orbite est synchronisée avec un jour réel latéral (c’est-à-dire 23 heures 56 minutes). Cette orbite peut avoir une inclinaison et une excentricité. Elle peut ne pas être circulaire. Cette orbite peut être inclinée aux pôles de la terre. Mais elle apparaît stationnaire lorsqu’elle est observée depuis la Terre.
La même orbite géo-synchrone, si elle est circulaire et dans le plan de l’équateur, elle est appelée orbite géo-stationnaire. Ces satellites sont placés à 35 900kms (comme les géosynchrones) au-dessus de l’équateur de la Terre et ils continuent à tourner par rapport à la direction de la Terre (d’ouest en est). Ces satellites sont considérés comme stationnaires par rapport à la terre, d’où leur nom.
Les satellites à orbite terrestre géostationnaire sont utilisés pour les prévisions météorologiques, la télévision par satellite, la radio par satellite et d’autres types de communications mondiales.
La figure suivante montre la différence entre les orbites géosynchrones et géostationnaires. L’axe de rotation indique le mouvement de la Terre.
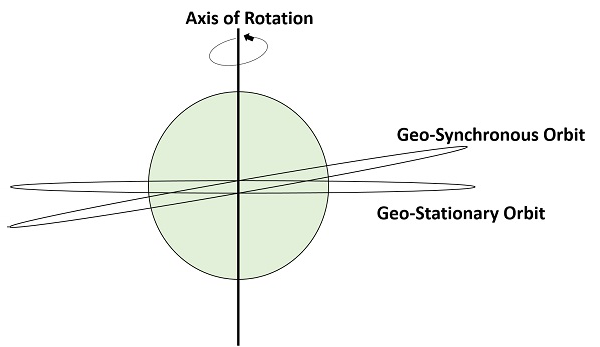
Note – Chaque orbite géo-stationnaire est une orbite géo-synchrone. Mais chaque orbite géo-synchrone n’est PAS une orbite géo-stationnaire.
Satellites à orbite terrestre moyenne
Les réseaux de satellites à orbite terrestre moyenne (MEO) orbitent à des distances d’environ 8000 miles de la surface de la Terre. Les signaux transmis depuis un satellite MEO parcourent une distance plus courte. Cela se traduit par une amélioration de la puissance du signal à l’extrémité réceptrice. Cela montre que des terminaux de réception plus petits et plus légers peuvent être utilisés à l’extrémité de réception.
Puisque le signal parcourt une distance plus courte vers et depuis le satellite, il y a moins de retard de transmission. Le délai de transmission peut être défini comme le temps qu’il faut à un signal pour monter jusqu’à un satellite et redescendre jusqu’à une station de réception.
Pour les communications en temps réel, plus le délai de transmission est court, meilleur sera le système de communication. A titre d’exemple, si un satellite GEO nécessite 0,25 seconde pour un aller-retour, alors le satellite MEO nécessite moins de 0,1 seconde pour effectuer le même trajet. Les MEO fonctionnent dans la gamme de fréquences de 2 GHz et plus.
Satellites à orbite basse
Les satellites à orbite basse (LEO) sont principalement classés en trois catégories à savoir, les petits LEO, les grands LEO et les Mega-LEO. Les LEO seront en orbite à une distance de 500 à 1000 miles au-dessus de la surface de la terre.
Cette distance relativement courte réduit le délai de transmission à seulement 0,05 seconde. Cela réduit encore le besoin d’équipements de réception sensibles et encombrants. Les petits LEO fonctionneront dans la gamme des 800 MHz (0,8 GHz). Les Big LEOs fonctionneront dans la gamme des 2 GHz ou plus, et les Mega-LEOs fonctionnent dans la gamme des 20-30 GHz.
Les fréquences plus élevées associées aux Mega-LEOs se traduisent par une plus grande capacité de transport d’informations et cèdent à la capacité du schéma de transmission vidéo en temps réel et à faible délai.
La figure suivante représente les trajectoires des LEO, MEO et GEO.
.