
La question politique : Crédit d’impôt pour l’achat de voitures hybrides-Est-ce le meilleur choix du gouvernement pour réduire la consommation de carburant et les émissions de carbone ?
Les résidents américains et le gouvernement sont préoccupés par la dépendance au pétrole étranger importé et le rejet de carbone dans l’atmosphère. En 2005, le Congrès a adopté une loi visant à fournir aux consommateurs des crédits d’impôt pour l’achat de voitures électriques et hybrides.
Ce crédit d’impôt peut sembler être un bon choix politique, mais il est coûteux car il diminue directement le montant des recettes perçues par le gouvernement américain. Existe-t-il des approches plus efficaces pour réduire la dépendance aux combustibles fossiles et les émissions de carbone ? Comment décider quelle politique est la meilleure ? Pour répondre à cette question, les décideurs politiques doivent prédire avec une certaine précision comment les consommateurs réagiront à cette politique fiscale avant que ces décideurs politiques ne dépensent des millions de dollars fédéraux.
Nous pouvons appliquer le concept d’utilité à cette question politique. Dans ce module, nous allons étudier l’utilité et les fonctions d’utilité. Nous serons ensuite en mesure d’utiliser une fonction d’utilité appropriée pour dériver des courbes d’indifférence qui décrivent notre question de politique.
Exploration de la question de politique
Supposons que le crédit d’impôt visant à subventionner l’achat de voitures hybrides connaisse un succès fou et double l’économie moyenne de carburant de toutes les voitures sur les routes américaines – un résultat qui n’est clairement pas réaliste mais utile pour nos discussions ultérieures. À votre avis, qu’adviendrait-il de la consommation de carburant de tous les automobilistes américains ? Le gouvernement devrait-il s’attendre à ce que la consommation de carburant et les émissions de carbone des voitures diminuent de moitié en réponse ? Pourquoi ou pourquoi pas ?
2.1 Fonctions d’utilité
LO 2.1 : Décrire une fonction d’utilité.
2.2 Fonctions d’utilité et préférences typiques
LO 2.2 : Identifier les fonctions d’utilité en fonction des préférences typiques qu’elles représentent.
2.3 Relier les fonctions d’utilité et les cartes de courbes d’indifférence
LO 2.3 : Expliquer comment dériver une courbe d’indifférence à partir d’une fonction d’utilité.
2.4 Trouver l’utilité marginale et le taux marginal de substitution
LO 2.4 : Dériver l’utilité marginale et le MRS pour des fonctions d’utilité typiques.
2.5. Question de politique générale
2.1 Fonctions d’utilité
LO1 : Décrire une fonction d’utilité.
Nos préférences nous permettent de faire des comparaisons entre différents ensembles de consommation et de choisir les ensembles préférés. Nous pourrions, par exemple, déterminer le classement de tout un ensemble de bouquets de consommation en fonction de nos préférences. Une fonction d’utilité est une fonction mathématique qui permet de classer des ensembles de biens de consommation en leur attribuant un chiffre, les chiffres les plus élevés correspondant aux ensembles préférés. Les fonctions d’utilité possèdent les propriétés que nous avons identifiées dans le module 1 concernant les préférences. C’est-à-dire : elles sont capables d’ordonner des regroupements, elles sont complètes et transitives, plus est préféré à moins et, dans des cas pertinents, les regroupements mixtes sont meilleurs.
Le nombre que la fonction d’utilité attribue à un regroupement spécifique est connu sous le nom d’utilité, la satisfaction qu’un consommateur obtient d’un regroupement spécifique. Le nombre d’utilité pour chaque ensemble ne signifie rien en termes absolus ; il n’y a pas d’échelle uniforme par rapport à laquelle nous mesurons la satisfaction. Sa seule utilité est en termes relatifs : nous pouvons utiliser l’utilité pour déterminer quels regroupements sont préférés à d’autres.
Si l’utilité du regroupement A est supérieure à l’utilité du regroupement B, cela revient à dire que le consommateur préfère le regroupement A au regroupement B. Les fonctions d’utilité classent donc les préférences des consommateurs en attribuant un nombre à chaque regroupement. . Nous pouvons utiliser une fonction d’utilité pour dessiner les cartes des courbes d’indifférence décrites dans le module 1. Étant donné que tous les lots de la même courbe d’indifférence procurent la même satisfaction, et qu’aucun n’est donc préféré, chaque lot a la même utilité. Nous pouvons donc dessiner une courbe d’indifférence en déterminant tous les regroupements qui renvoient le même nombre de la fonction d’utilité.
Les économistes disent que les fonctions d’utilité sont ordinales plutôt que cardinales. Ordinale signifie que les fonctions d’utilité ne font que classer les regroupements – elles indiquent seulement lequel est meilleur, pas combien il est meilleur qu’un autre regroupement. Supposons, par exemple, qu’une fonction d’utilité indique que le lot A rapporte 10 utils et le lot B 20 utils. Nous ne disons pas que l’offre B est deux fois plus intéressante, ou qu’elle est meilleure de 10 utils, mais seulement que le consommateur préfère l’offre B. Par exemple, supposons qu’une amie participe à une course et vous dise qu’elle est arrivée troisième. Cette information est ordinale : Vous savez qu’elle était plus rapide que le coureur arrivé en quatrième position et plus lente que le coureur arrivé en deuxième position. Vous ne connaissez que l’ordre dans lequel les coureurs ont terminé. Les temps individuels sont cardinaux : Si le coureur arrivé en première position a couru la course en exactement une heure et que votre ami a terminé en une heure et six minutes, vous savez que votre ami était exactement 10 % plus lent que le coureur le plus rapide. Ceci est vrai tant que l’ordre est préservé.
Prenons par exemple la fonction d’utilité U qui décrit les préférences sur des ensembles de biens A abd B : U(A,B). Nous pouvons appliquer n’importe quelle transformation monotone positive à cette fonction (ce qui signifie, essentiellement, que nous ne changeons pas l’ordonnancement) et la nouvelle fonction que nous avons créée représentera les mêmes préférences. Par exemple, nous pouvons multiplier une constante positive, α , ou ajouter une constante positive ou négative, β . Ainsi, αU(A,B)+β représente exactement les mêmes préférences que U(A,B) car elle ordonne les paquets exactement de la même manière. Ce fait est assez utile car parfois, appliquer une transformation monotone positive d’une fonction d’utilité facilite la résolution de problèmes.
2.2 Fonctions d’utilité et préférences typiques
LO2 : Identifier les fonctions d’utilité en fonction des préférences typiques qu’elles représentent
Considérons des paquets de pommes, A, et de bananes, B. Une fonction d’utilité qui décrit les préférences d’Isaac pour les paquets de pommes et de bananes est la fonction U(A,B). Mais quelles sont les préférences particulières d’Isaac pour les paquets de pommes et de bananes ? Supposons qu’Isaac ait des préférences assez classiques pour les pommes et les bananes, qui conduisent à nos courbes d’indifférence typiques : Il préfère le plus au moins, et il aime la variété. Une fonction d’utilité qui représente ces préférences pourrait être :
U(A,B) = AB
Si les pommes et les bananes sont des compléments parfaits dans les préférences d’Isaac, la fonction d’utilité ressemblerait à ceci :
U(A,B) = MIN,
où la fonction MIN attribue simplement le plus petit des deux nombres comme valeur de la fonction.
Si les pommes et les bananes sont des substituts parfaits, la fonction d’utilité est additive et ressemblerait à quelque chose comme ceci :
U(A,B) = A + B
Une classe de fonctions d’utilité connue sous le nom de fonctions d’utilité Cobb-Douglas est très couramment utilisée en économie pour deux raisons :
1. Elles représentent des préférences » bien conduites « , telles que plus c’est mieux et la préférence pour la variété.
2. Elles sont très flexibles et peuvent être ajustées pour s’adapter très facilement aux données du monde réel.
Les fonctions d’utilité de Cobb-Douglas ont cette forme:
U(A,B) = AαBβ
Parce que les transformations monotones positives représentent les mêmes préférences, une telle transformation peut être utilisée pour fixer α + β = 1 , ce que nous verrons plus tard est une condition pratique qui simplifie certains calculs dans le problème du choix du consommateur.
Une autre façon de transformer la fonction d’utilité d’une manière utile est de prendre le log naturel de la fonction, ce qui crée une nouvelle fonction qui ressemble à ceci :
U(A,B) = αln(A) + βln(B)
Pour dériver cette équation, il suffit d’appliquer les règles des logs naturels . Il est important de garder à l’esprit le niveau d’abstraction ici. Nous ne pouvons généralement pas faire de fonctions d’utilité spécifiques qui décrivent précisément les préférences individuelles. Il est probable qu’aucun d’entre nous ne pourrait décrire ses propres préférences à l’aide d’une seule équation. Mais tant que les consommateurs en général ont des préférences qui suivent nos hypothèses de base, nous pouvons faire un assez bon travail en trouvant des fonctions d’utilité qui correspondent aux données de consommation du monde réel. Nous en verrons la preuve plus tard dans le cours.
Le tableau 2.1 résume les préférences et les fonctions d’utilité décrites dans cette section.
|
Tableau 2.1 Types de préférences et les fonctions d’utilité qui les représentent |
||
|
Préférences |
FONCTION D’UTILITE. FONCTION |
TYPE DE FONCTION UTILITAIRE |
|
Amour de la variété ou « bien élevé » |
U(A.,B) = AB |
Cobb-Douglas |
|
Amour de la variété ou « bien élevé » |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Amour de la variété ou « bien élevé » |
U(A,B) = αln(A) + βln(B) |
Logar naturel Cobb-Douglas |
|
Compléments parfaits |
U(A,B) = MIN |
Fonction Min |
|
Substituts parfaits |
U(A,B) = A + B |
Additif |
2.3 Relier les fonctions d’utilité et les cartes de courbes d’indifférence
LO3 : Expliquer comment dériver une courbe d’indifférence à partir d’une fonction d’utilité
Les courbes d’indifférence et les fonctions d’utilité sont directement liées. En fait, puisque les courbes d’indifférence représentent les préférences graphiquement et les fonctions d’utilité mathématiquement, il s’ensuit que les courbes d’indifférence peuvent être dérivées des fonctions d’utilité.
Dans les fonctions uni-variées, la variable dépendante est tracée sur l’axe vertical et la variable indépendante est tracée sur l’axe horizontal, comme le graphique de y=f(x). En revanche, les graphiques des fonctions à deux variables sont tridimensionnels, comme U=U(A,B). La figure 2.1 montre un graphique de U=A^\frac{1}{2}B^\frac{1}{2}. Les graphiques tridimensionnels sont utiles pour comprendre comment l’utilité augmente avec l’augmentation de la consommation de A et B.
Figure 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
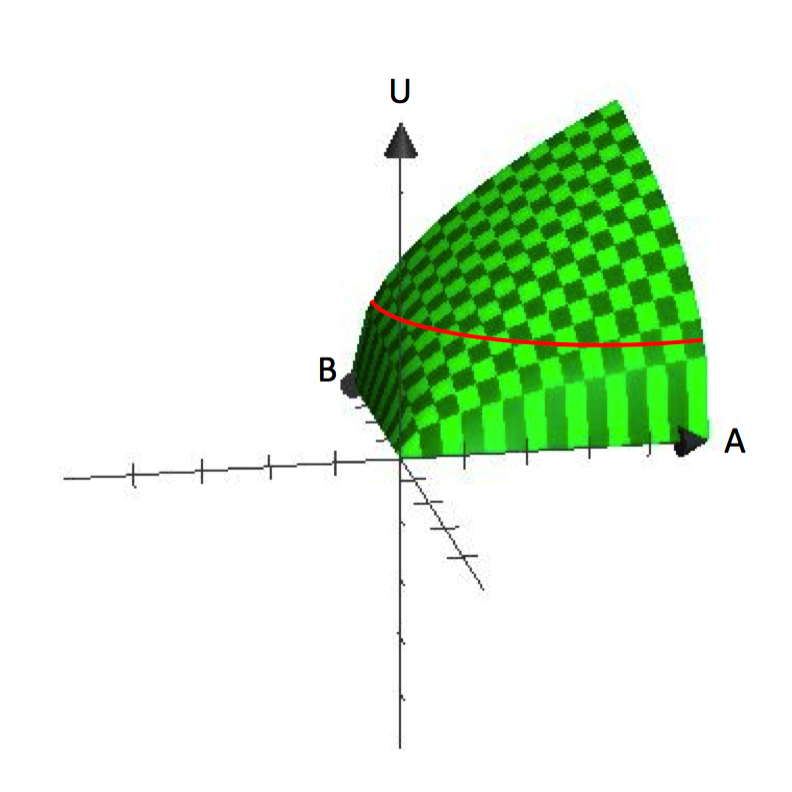
La figure 2.1 montre clairement l’hypothèse selon laquelle les consommateurs ont une préférence pour la variété. Chaque paquet qui contient une quantité spécifique de A et B représente un point sur la surface. La hauteur verticale de la surface représente le niveau d’utilité. En augmentant à la fois A et B, un consommateur peut atteindre des points plus élevés sur la surface.
Alors, d’où viennent les courbes d’indifférence ? Rappelons qu’une courbe d’indifférence est un ensemble de tous les forfaits auxquels un consommateur est indifférent, par rapport à celui qu’il doit consommer. Mathématiquement, cela revient à dire que toutes les offres, lorsqu’elles sont intégrées dans la fonction d’utilité, renvoient la même valeur fonctionnelle. Ainsi, si nous fixons une valeur pour l’utilité, Ū, et que nous trouvons tous les paquets de A et B qui génèrent cette valeur, nous définirons une courbe d’indifférence. Remarquez que cela revient à trouver tous les faisceaux qui amènent le consommateur à la même hauteur sur la surface tridimensionnelle de la figure 2.1.
Les courbes d’indifférence sont une représentation de l’élévation (niveau d’utilité) sur une surface plane. En ce sens, elles sont analogues à une courbe de niveau sur une carte topographique. En ramenant le graphique tridimensionnel à un espace bidimensionnel – l’espace A, B – nous pouvons montrer les lignes de contour/courbes d’indifférence qui représentent différentes élévations ou niveaux d’utilité. À partir du graphique de la figure 2.1, vous pouvez déjà voir comment cette fonction d’utilité donne des courbes d’indifférence qui sont » arquées » ou concaves par rapport à l’origine.
Les courbes d’indifférence découlent donc directement des fonctions d’utilité et constituent un moyen utile de représenter les fonctions d’utilité dans un graphique à deux dimensions.
2.4 Trouver l’utilité marginale et le taux marginal de substitution
LO4 : Dériver l’utilité marginale et le MRS pour des fonctions d’utilité typiques.
L’utilité marginale est l’utilité supplémentaire qu’un consommateur reçoit en consommant une unité supplémentaire d’un bien. Mathématiquement, nous l’exprimons ainsi :
MU_{a}=\frac{\Delta \cup }{\Delta A}
ou le changement d’utilité provenant d’un changement de la quantité de A consommée, où Δ représente un changement de la valeur de l’article. Ainsi,
MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Notez que lorsque nous examinons l’utilité marginale de la consommation de A, nous maintenons B constant.
En utilisant le calcul, l’utilité marginale est la même que la dérivée partielle de la fonction d’utilité par rapport à A:
MU_{A}\frac{\partial U(A,B)}{\partial A}
Considérons un consommateur qui s’assied pour manger un repas composé de salade et de pizza. Supposons que nous maintenions la quantité de salade constante – une salade d’accompagnement avec un dîner, par exemple. Augmentons maintenant le nombre de tranches de pizza : supposons que l’utilité d’une tranche est de 10, de 18 avec 2, de 24 avec 3 et de 28 avec 4. Traçons ces chiffres sur un graphique ayant l’utilité sur l’axe vertical et la pizza sur l’axe horizontal (figure 2.2).
Figure 2.2 : Graphique et tableau de l’utilité marginale décroissante
|
Pizza Slices |
Utilité |
Marginale. Utilité |
|
1 |
10 |
|
|
2 |
18 |
8 |
|
3 |
24 |
6 |
|
4 |
28 |
4 |
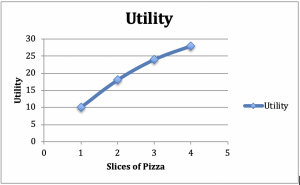
D’après la pente positive du graphique, nous pouvons voir l’augmentation de l’utilité des parts supplémentaires de pizza. À partir de la forme concave du graphique, nous pouvons voir un autre phénomène commun : L’utilité supplémentaire que le consommateur reçoit de chaque part de pizza supplémentaire diminue avec le nombre de parts consommées.
Le fait que l’utilité supplémentaire diminue avec chaque part de pizza supplémentaire est appelé le principe de l’utilité marginale décroissante. Ce principe s’applique à des préférences bien conduites où les paquets mixtes sont préférés.
Le taux marginal de substitution (TMS) est la quantité d’un bien qu’un consommateur est prêt à abandonner pour obtenir une unité supplémentaire d’un autre bien. C’est pourquoi c’est la même chose que la pente de la courbe d’indifférence – puisque nous gardons le niveau de satisfaction constant, nous restons sur la même courbe d’indifférence, nous nous déplaçons simplement le long de celle-ci lorsque nous échangeons un bien contre un autre. La quantité de l’un que vous êtes prêt à échanger contre un plus d’un autre dépend de l’utilité marginale de chacun.
En reprenant notre exemple précédent, si en consommant une salade latérale de plus votre utilité augmente de 10, alors à une consommation actuelle de 4 parts de pizza, vous pourriez renoncer à 2 parts de pizza et passer de 28 à 18 utils. Si l’on ajoute 10 utilités à la salade et que l’on diminue de 10 utilités en renonçant à 2 parts de pizza, l’utilité globale reste inchangée – nous sommes donc toujours sur la même courbe d’indifférence. Lorsque vous vous déplacez le long de la courbe d’indifférence, vous devez suivre la pente, c’est-à-dire que vous devez abandonner le bien sur l’axe vertical pour plus de bien sur l’axe horizontal, ce qui donne une hausse négative sur une course positive.
Nous pouvons passer directement de l’utilité marginale au SRM en reconnaissant le lien entre les deux concepts. Dans notre cas, pour une fonction d’utilité U=U(A,B) , la MRS est représentée par :
MRS=-\frac{MU_{A}}{MU_{B}}
Notez que lorsque nous substituons nous pouvons simplifier l’équation :
MRS=-\frac{MU_{A}{MU_{B}}=-\frac{\frac{\Delta U}{\Delta A}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}
En insérant le calcul, cela équivaut à :
MRS=-\frac{\frac{\partial U(A,B)}{\partial A}}{\frac{\partial U(A,B)}{\partial B}}
2.5 Question de politique
Nous avons déterminé dans le module 1 que la décision pertinente du consommateur entre plus de kilomètres parcourus et d’autres consommations est probablement conforme aux hypothèses standard sur le choix du consommateur. Par conséquent, l’utilisation de la fonction d’utilité Cobb-Douglas pour représenter un consommateur qui aime conduire une voiture ainsi que consommer d’autres biens, et qui les considère comme un compromis (l’argent dépensé pour l’essence est de l’argent non dépensé pour d’autres biens de consommation), est un bon choix. Il a aussi l’avantage à la fois de se conformer aux hypothèses, et d’être flexible :
U(MD,C)=MD^{a}C^{\beta }.
où MD = kilomètres parcourus, et C = autre consommation.
En fait, la fonction elle-même peut être ramenée à des données du monde réel où les paramètres et peuvent être estimés pour ce marché, le marché des kilomètres parcourus dans la voiture du consommateur.
Figure 2.3 Graphique des courbes d’indifférence pour l’exemple de politique
Exploration des questions de politique:
1 . D’autres types de préférence seraient-ils plus appropriés dans cet exemple ?
2. Qu’est-ce qui devrait être vrai pour que les compléments parfaits soient le type de préférence approprié à utiliser pour analyser cette politique ?
Qu’est-ce qui devrait être vrai pour les substituts parfaits ? Étant donné que nous considérons un consommateur » typique » qui conduit, est-il approprié de choisir une fonction d’utilité » typique » ?
4. Sommes-nous simplement en train de deviner ou avons-nous une base théorique pour soutenir notre choix de préférences » bien conduites » ou une fonction d’utilité Cobb-Douglas ?
Résumé
Revue : Sujets et résultats d’apprentissage connexes
2.1 Fonctions d’utilité
LO 2.1 : Décrire une fonction d’utilité
2.2 Fonctions d’utilité et préférences typiques
LO 2.2 : Identifier les fonctions d’utilité en fonction des préférences typiques qu’elles représentent
2.3 Relier les fonctions d’utilité et les cartes de courbes d’indifférence
LO 2.3 : Expliquer comment dériver une courbe d’indifférence à partir d’une fonction d’utilité
2.4 Trouver l’utilité marginale et le taux marginal de substitution
LO 2.4 : Dériver l’utilité marginale et le MRS pour des fonctions d’utilité typiques.
2.5. Question de politique générale
Apprendre : Termes clés et graphiques
Les bivariate functions
Cardinal
Contour line
Diminishing marginal utility
Function
Marginal rate of substitution (MRS)
Marginal utility
.
Ordinale
Fonctions univariées
Util
Utilité
Fonction d’utilité
Graphes
Fonction d’utilité 3D et courbe de niveau
Equations
Cobb-.Douglas
Compléments parfaits
Substituts parfaits
.