L’étude des jeux est l’étude de l’interaction stratégique où la décision d’un joueur dépend de ce que fait l’autre joueur. Ce que fait l’adversaire dépend également de ce qu’il pense que le premier joueur fera.
Exemples de la théorie des jeux
- Les deux joueurs ont une stratégie dominante.
Une stratégie dominante se produit lorsqu’il existe un choix optimal de stratégie pour chaque joueur, peu importe ce que fait l’autre.
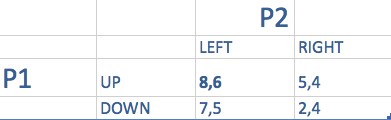
- Si P2 choisit à gauche, P1 choisira UP
- Si P2 choisit à droite, P1 choisira UP
- Donc UP est une stratégie dominante pour P1
P2 choisira toujours à droite quoi que fasse P1
L’unique équilibre est (up, left). C’est le meilleur pour les deux
- Un joueur a une stratégie dominante
PIGLET
Pousser le levier attendre le swill
Pousser le levier 8,-2 1,7
PIG
Attendre le swill 10,-2 0,0
- Le cochon attendra toujours
- Le cochon devra pousser
Equilibre de Nash
Il existe de nombreux jeux qui n’ont pas de stratégie dominante.
Définition : Un équilibre de Nash se produit lorsque le gain du joueur un est le meilleur étant donné le choix de l’autre.
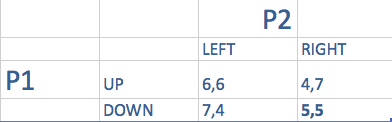
Dans ce cas Si P1 choisit vers le bas, P2 choisira à droite
Si P1 choisit vers le haut, P2 choisira à droite. Mais, si P2 choisit droit, P1 voudra choisir bas.
L’équilibre de Nash sera bas droit, (5,5) malgré le fait que UP gauche soit le résultat optimal de Pareto.
Collusion et théorie des jeux
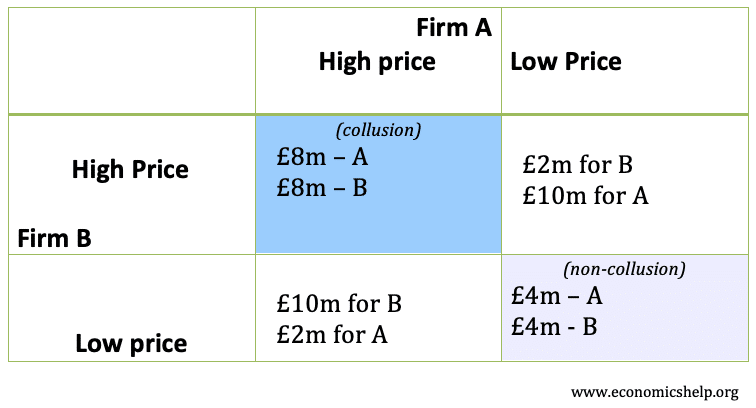
- Si les entreprises sont compétitives et qu’elles fixent un prix bas -elles feront toutes deux 4m£.
- Si elles s’entendent et fixent un prix élevé, alors elles doubleront toutes deux leurs bénéfices et gagneront 8 millions de livres sterling.
- Cependant, si pendant la collusion, l’entreprise A sous-estime le prix collusoire et fixe un prix bas – elle est capable de vendre plus. Dans ce cas, l’entreprise A bénéficie du meilleur des deux mondes. Les prix sont élevés parce que l’entreprise B fixe un prix élevé, mais l’entreprise A vend également de grandes quantités parce qu’elle vend moins cher que son rival. Dans ce cas, l’entreprise A fait 10 millions de livres sterling et l’entreprise B ne fait que 2 millions de livres sterling.
- Donc, il est peu probable que l’entreprise B maintienne des prix élevés et le marché revient à ce que les deux fixent des prix bas.
Le résultat optimal pour les entreprises est de s’entendre (prix élevé, prix élevé)
Jeux répétés et théorie des jeux
Si les jeux sont répétés, alors il y a la possibilité de punir les gens qui trichent, cela incitera à s’en tenir à l’approche optimale de Pareto.
En revanche, s’ils sont répétés un nombre fini de fois, alors il y aura une incitation à tricher. Si le jeu est répété 10 fois alors le joueur fera défection au 10ème tour alors pourquoi coopérer. Donc, par conséquent, autant faire défection au 9ème tour et donc au 8ème tour également
S’il est joué un nombre infini de fois alors ce sera différent. La meilleure stratégie est alors de jouer au chat et à la souris. Si un joueur fait défaut dans un tour, vous ripostez dans le tour suivant. En d’autres termes, vous faites tout ce que votre adversaire fait et cela incite à faire respecter le cartel.
Théorie des jeux : Un jeu de dissuasion d’entrée
Si une nouvelle entreprise entre sur le marché alors le gain dépendra du fait que l’opérateur historique se batte ou accepte. Si l’entreprise en place se bat, elles obtiennent toutes les deux 0. Si elle ne se bat pas, l’entreprise en place obtient 1 et l’entrant obtient 2. Par conséquent, l’équilibre est que la nouvelle entreprise entre et que l’opérateur historique accepte.
Cependant, si l’opérateur historique peut menacer de manière crédible qu’il se battra, il peut être en mesure de persuader l’entrant de rester en dehors. Il pourrait le faire en investissant dans des capacités supplémentaires, ce qui lui donnerait un gain plus important dans une guerre des prix. Cela dissuaderait l’entrée. Donc, bien que le monopoliste n’utiliserait jamais cela, il empêcherait l’entrée.
Théorie des jeux et courbe de demande coudée
La théorie des jeux peut être utilisée pour les stratégies de prix.
En oligopole, les entreprises peuvent décider de baisser les prix, de les augmenter ou de les garder statiques.
Le modèle de la courbe de demande coudée suggère que le résultat le plus probable est la stabilité des prix. Cela est dû au fait que
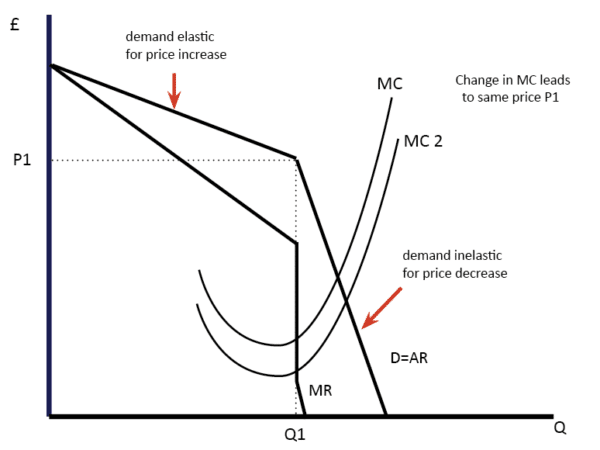
- Si les entreprises augmentent le prix, les autres ne le font pas – Par conséquent, la demande chute de manière significative. (La demande est élastique)
- Si les entreprises baissent le prix, vous gagneriez une augmentation de la part de marché. Les autres entreprises ne veulent pas permettre cela. Par conséquent, elles réduisent également leurs prix. En gros, cela provoque une guerre des prix où tout le monde est perdant.
Donc, en oligopole, une caractéristique importante des décisions des entreprises est l’impact de l’interdépendance. Les décisions d’une entreprise ont un impact significatif sur les autres.
Related
- Théorie des jeux – réduire le prix des playstations
.