L’écart type est la quantité moyenne de variabilité dans votre ensemble de données. Il vous indique, en moyenne, à quelle distance chaque valeur se situe par rapport à la moyenne.
Un écart-type élevé signifie que les valeurs sont généralement éloignées de la moyenne, tandis qu’un écart-type faible indique que les valeurs sont regroupées près de la moyenne.
Que vous dit l’écart-type ?
L’écart-type est une mesure utile de la dispersion pour les distributions normales.
Dans les distributions normales, les données sont distribuées de manière symétrique et sans biais. La plupart des valeurs se regroupent autour d’une région centrale, les valeurs s’amenuisant à mesure qu’elles s’éloignent du centre. L’écart-type vous indique à quel point vos données sont en moyenne éloignées du centre de la distribution.
De nombreuses variables scientifiques suivent des distributions normales, notamment la taille, les résultats de tests standardisés ou les taux de satisfaction au travail. Lorsque vous disposez des écarts types de différents échantillons, vous pouvez comparer leurs distributions à l’aide de tests statistiques afin de faire des inférences sur les populations plus importantes dont ils sont issus.
Les notes moyennes (M) sont les mêmes pour chaque groupe – c’est la valeur sur l’axe des x lorsque la courbe est à son sommet. Cependant, leurs écarts types (ET) diffèrent les uns des autres.
L’écart type reflète la dispersion de la distribution. La courbe avec l’écart-type le plus faible a un pic élevé et une petite dispersion, tandis que la courbe avec l’écart-type le plus élevé est plus plate et plus étendue.
La règle empirique
L’écart-type et la moyenne ensemble peuvent vous indiquer où se situent la plupart des valeurs de votre distribution si elles suivent une distribution normale.
La règle empirique, ou la règle 68-95-99,7, vous indique où se situent vos valeurs :
- Environ 68% des scores se situent à 2 écarts types de la moyenne,
- Environ 95% des scores se situent à 4 écarts types de la moyenne,
- Environ 99.7% des scores sont dans les 6 écarts types de la moyenne.
Suivant la règle empirique :
- Environ 68% des scores sont compris entre 40 et 60.
- Environ 95% des scores sont compris entre 30 et 70.
- Environ 99,7% des scores sont compris entre 20 et 80.
La règle empirique est un moyen rapide d’avoir une vue d’ensemble de vos données et de vérifier s’il existe des valeurs aberrantes ou extrêmes qui ne suivent pas ce modèle.
Pour les distributions non normales, l’écart type est une mesure moins fiable de la variabilité et devrait être utilisé en combinaison avec d’autres mesures comme l’étendue ou l’écart interquartile.
Formules d’écart type pour les populations et les échantillons
Des formules différentes sont utilisées pour calculer les écarts types selon que vous avez des données provenant d’une population entière ou d’un échantillon.
Ecart-type de la population
Lorsque vous avez recueilli des données de chaque membre de la population qui vous intéresse, vous pouvez obtenir une valeur exacte pour l’écart-type de la population.
La formule de l’écart-type de la population ressemble à ceci :
| Formule | Explication |
|---|---|
 |
|
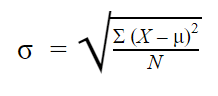Ecart-type de l’échantillon
Lorsque vous recueillez des données à partir d’un échantillon, l’écart-type de l’échantillon est utilisé pour faire des estimations ou des inférences sur l’écart-type de la population.
La formule de l’écart type de l’échantillon se présente comme suit :
| Formule | Explication |
|---|---|
 |
|
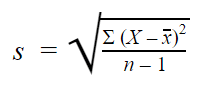Avec les échantillons, nous utilisons n – 1 dans la formule parce que l’utilisation de n nous donnerait une estimation biaisée qui sous-estime constamment la variabilité. L’écart type de l’échantillon aurait tendance à être plus faible que l’écart type réel de la population.
Réduire l’échantillon n à n – 1 rend l’écart type artificiellement grand, ce qui vous donne une estimation conservatrice de la variabilité.
Bien que ce ne soit pas une estimation sans biais, c’est une estimation moins biaisée de l’écart-type : il vaut mieux surestimer que sous-estimer la variabilité des échantillons.
Étapes du calcul de l’écart-type
L’écart-type est généralement calculé automatiquement par le logiciel que vous utilisez pour votre analyse statistique. Mais vous pouvez aussi le calculer à la main pour mieux comprendre comment fonctionne la formule.
Il y a six étapes principales pour trouver l’écart-type à la main. Nous allons utiliser un petit ensemble de données de 6 scores pour parcourir les étapes.
| Ensemble de données | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Étape 1 : Trouvez la moyenne
Pour trouver la moyenne, additionnez toutes les notes, puis divisez-les par le nombre de notes.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Étape 2 : Trouver l’écart de chaque score par rapport à la moyenne
Soustraire la moyenne de chaque score pour obtenir les écarts par rapport à la moyenne.
Puisque x̅ = 50, ici on enlève 50 à chaque score.
| Score | Ecart par rapport à la moyenne |
|---|---|
| 46 | 46 – 50 = -.4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Etape 3 : Élevez au carré chaque écart par rapport à la moyenne
Multipliez chaque écart par rapport à la moyenne par lui-même. Cela donnera des nombres positifs.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -.18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Étape 4 : Trouvez la somme des carrés
Ajoutez tous les écarts au carré. C’est ce qu’on appelle la somme des carrés.
16 + 361 + 324 + 100 + 4 + 81 = 886
Étape 5 : Trouver la variance
Diviser la somme des carrés par n – 1 (pour un échantillon) ou N (pour une population) – c’est la variance.
Puisque nous travaillons avec un échantillon de 6, nous utiliserons n – 1, où n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Étape 6 : Trouver la racine carrée de la variance
Pour trouver l’écart-type, nous prenons la racine carrée de la variance.
√177,2 = 13,31
En apprenant que SD = 13.31, nous pouvons dire que chaque score s’écarte de la moyenne de 13,31 points en moyenne.
Pourquoi l’écart-type est-il une mesure utile de la variabilité ?
Bien qu’il existe des moyens plus simples de calculer la variabilité, la formule de l’écart-type pèse davantage sur les échantillons inégalement répartis que sur les échantillons uniformément répartis. Un écart-type plus élevé vous indique que la distribution est non seulement plus étalée, mais aussi plus inégalement répartie.
Cela signifie qu’il vous donne une meilleure idée de la variabilité de vos données que des mesures plus simples, telles que l’écart absolu moyen (MAD).
Le MAD est similaire à l’écart-type mais plus facile à calculer. D’abord, vous exprimez chaque écart par rapport à la moyenne en valeurs absolues en les convertissant en nombres positifs (par exemple, -3 devient 3). Ensuite, vous calculez la moyenne de ces écarts absolus.
Contrairement à l’écart-type, vous n’avez pas à calculer les carrés ou les racines carrées des nombres pour le MAD. Cependant, pour cette raison, il vous donne une mesure moins précise de la variabilité.
Prenons deux échantillons ayant la même tendance centrale mais des quantités différentes de variabilité. L’échantillon B est plus variable que l’échantillon A.
| Valeurs | Moyenne | Écart absolu moyen | Écart-type | |
|---|---|---|---|---|
| Échantillon A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| Échantillon B | 51, 21, 79, 49 | 50 | 15 | 23,7 |
Pour des échantillons dont les écarts moyens par rapport à la moyenne sont égaux, le MAD ne permet pas de différencier les niveaux de dispersion. L’écart-type est plus précis : il est plus élevé pour l’échantillon dont les écarts par rapport à la moyenne sont plus variables.
En élevant au carré les écarts par rapport à la moyenne, l’écart-type reflète plus précisément la dispersion inégale. Cette étape pèse plus lourdement les écarts extrêmes que les petits écarts.
Cependant, cela rend également l’écart-type sensible aux valeurs aberrantes.
Questions fréquemment posées sur l’écart-type
La variabilité est le plus souvent mesurée avec les statistiques descriptives suivantes :
- Etendue : la différence entre les valeurs les plus élevées et les plus basses
- Etendue interquartile : l’étendue de la moitié médiane d’une distribution
- Écart-type : distance moyenne par rapport à la moyenne
- Variance : moyenne des carrés des distances par rapport à la moyenne
L’écart-type est la quantité moyenne de variabilité dans votre ensemble de données. Il vous indique, en moyenne, à quelle distance de la moyenne se trouve chaque résultat.
Dans les distributions normales, un écart-type élevé signifie que les valeurs sont généralement éloignées de la moyenne, tandis qu’un écart-type faible indique que les valeurs sont regroupées près de la moyenne.
Dans une distribution normale, les données sont distribuées de manière symétrique et sans asymétrie. La plupart des valeurs se regroupent autour d’une région centrale, les valeurs diminuant au fur et à mesure qu’elles s’éloignent du centre.
Les mesures de tendance centrale (moyenne, mode et médiane) sont exactement les mêmes dans une distribution normale.
La règle empirique, ou règle des 68-95-99,7, vous indique où se situent la plupart des valeurs dans une distribution normale :
- Environ 68% des valeurs se situent à moins d’un écart-type de la moyenne.
- Environ 95% des valeurs se situent à moins de 2 écarts-types de la moyenne.
- Environ 99.7% des valeurs se situent à l’intérieur de 3 écarts-types de la moyenne.
La règle empirique est un moyen rapide d’avoir une vue d’ensemble de vos données et de vérifier si des valeurs aberrantes ou extrêmes ne suivent pas ce modèle.
La variance est la moyenne des écarts au carré par rapport à la moyenne, tandis que l’écart-type est la racine carrée de ce nombre. Les deux mesures reflètent la variabilité d’une distribution, mais leurs unités diffèrent :
- L’écart-type est exprimé dans les mêmes unités que les valeurs initiales (par exemple, les minutes ou les mètres).
- La variance est exprimée dans des unités beaucoup plus grandes (par exemple, les mètres au carré).
Bien que les unités de la variance soient plus difficiles à comprendre intuitivement, la variance est importante dans les tests statistiques.
.