Dans l’ère moderne de l’audio, vous ne pouvez pas bouger pour la mention de la musique « Hi-Res » et 24-bit « Studio Quality ». Si vous n’avez pas repéré la tendance dans les smartphones haut de gamme – le codec Bluetooth LDAC de Sony – et les services de streaming comme Tidal, alors vous devez vraiment commencer à lire davantage ce site.
La promesse est simple – une qualité d’écoute supérieure grâce à plus de données, alias la profondeur de bits. La promesse est simple : une qualité d’écoute supérieure grâce à une plus grande quantité de données, c’est-à-dire une profondeur de bits, soit 24 bits de bits et de zéros numériques contre 16 bits, vestige de l’ère du CD. Bien sûr, vous devrez payer un supplément pour ces produits et services de qualité supérieure, mais plus de bits, c’est sûrement mieux, n’est-ce pas ?
L’audio « basse résolution » est souvent présenté comme une forme d’onde en escalier. Ce n’est pas comme ça que l’échantillonnage audio fonctionne et ce n’est pas ce à quoi ressemble l’audio sortant d’un appareil.
Pas nécessairement. Le besoin de profondeurs de bits de plus en plus élevées n’est pas basé sur la réalité scientifique, mais plutôt sur une déformation de la vérité et l’exploitation d’un manque de sensibilisation des consommateurs à la science du son. En fin de compte, les entreprises qui commercialisent de l’audio 24 bits ont beaucoup plus à gagner en termes de profit que vous en termes de qualité de lecture supérieure.
Profondeur binaire et qualité sonore : L’escalier n’est pas une chose
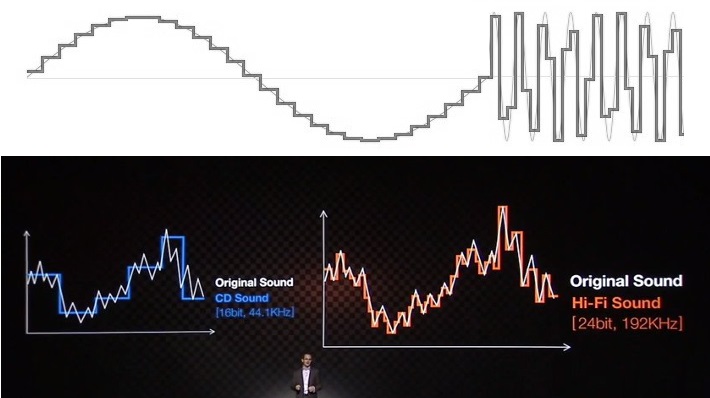
Pour suggérer que l’audio 24 bits est un must-have, les entreprises (et trop d’autres qui tentent d’expliquer ce sujet) trottent l’escalier très familier de la qualité audio vers le paradis. L’exemple 16 bits montre toujours une reproduction irrégulière et irrégulière d’une onde sinusoïdale ou d’un autre signal, tandis que l’équivalent 24 bits semble magnifiquement lisse et de plus haute résolution. Il s’agit d’une aide visuelle simple, mais qui s’appuie sur l’ignorance du sujet et de la science pour amener les consommateurs à des conclusions erronées.
Avant que quelqu’un ne m’arrache la tête, techniquement parlant, ces exemples d’escaliers dépeignent en quelque sorte fidèlement l’audio dans le domaine numérique. Cependant, un diagramme stem plot/lollipop est un graphique plus précis pour visualiser l’échantillonnage audio que ces marches d’escalier. Pensez-y de cette façon – un échantillon contient une amplitude à un moment très spécifique, pas une amplitude maintenue pendant une durée spécifique.

L’utilisation de graphiques en escalier est délibérément trompeuse alors que les diagrammes à tige fournissent une représentation plus précise de l’audio numérique. Ces deux graphiques tracent les mêmes points de données mais le graphique en escalier semble beaucoup moins précis.
Cependant, il est exact qu’un convertisseur analogique-numérique (CAN) doit faire rentrer un signal audio analogique infini dans un nombre fini de bits. Un bit qui se situe entre deux niveaux doit être arrondi à l’approximation la plus proche, ce qui est connu comme une erreur de quantification ou un bruit de quantification. (Retenez bien cela, car nous y reviendrons.)
Cependant, si vous regardez la sortie audio de n’importe quel convertisseur numérique-analogique (CNA) audio construit ce siècle (et probablement bien avant), vous ne repérerez aucune marche d’escalier. Pas même si vous sortez un signal de 8 bits. Alors qu’est-ce qui se passe ?

Une sortie d’onde sinusoïdale 8 bits, 10 kHz, capturée à partir d’un smartphone Pixel 3a à bas prix. Nous pouvons voir un peu de bruit, mais pas de marches d’escalier perceptibles si souvent dépeintes par les entreprises audio.
Premièrement, ce que ces diagrammes en escalier décrivent, si nous les appliquons à une sortie audio, est quelque chose appelé un CNA à maintien d’ordre zéro. C’est une technologie DAC très simple et bon marché où un signal est commuté entre différents niveaux à chaque nouvel échantillon pour donner une sortie. Cette technologie n’est utilisée dans aucun produit audio professionnel ou grand public à moitié décent. Vous pouvez la trouver dans un microcontrôleur à 5 $, mais certainement pas ailleurs. Déformer les sorties audio de cette façon implique une forme d’onde déformée et inexacte, mais ce n’est pas ce que vous obtenez.

En réalité, une sortie de DAC moderne ∆Σ est un signal PDM 1 bit suréchantillonné (à droite), plutôt qu’un signal de maintien à zéro (à gauche). Ce dernier produit une sortie analogique à faible bruit lorsqu’il est filtré.
Les CAN et les CNA de qualité audio sont principalement basés sur la modulation delta-sigma (∆Σ). Les composants de ce calibre comprennent l’interpolation et le suréchantillonnage, la mise en forme du bruit et le filtrage pour lisser et réduire le bruit. Les DAC Delta-sigma convertissent les échantillons audio en un flux de 1 bit (modulation de densité d’impulsion) avec une fréquence d’échantillonnage très élevée. Lorsqu’il est filtré, cela produit un signal de sortie lisse avec un bruit repoussé bien en dehors des fréquences audibles.
En un mot : les DAC modernes ne produisent pas d’échantillons audio déchiquetés d’apparence grossière – ils produisent un flux binaire qui est filtré par le bruit en une sortie très précise et lisse. Cette visualisation en escalier est fausse à cause de quelque chose appelé « bruit de quantification ».
Comprendre le bruit de quantification
Dans tout système fini, des erreurs d’arrondi se produisent. Il est vrai qu’un CAN ou un CNA de 24 bits aura une erreur d’arrondi plus petite qu’un équivalent de 16 bits, mais qu’est-ce que cela signifie réellement ? Plus important encore, qu’entendons-nous réellement ? S’agit-il de distorsion ou de fuzz, les détails sont-ils perdus à jamais ?
C’est en fait un peu des deux selon que l’on se trouve dans le domaine numérique ou analogique. Mais le concept clé pour comprendre les deux est de s’attaquer au plancher de bruit, et comment celui-ci s’améliore à mesure que la profondeur de bit augmente. Pour le démontrer, prenons du recul par rapport à 16 et 24 bits et regardons des exemples de très petite profondeur de bits.
La différence entre les profondeurs de 16 et 24 bits n’est pas la précision dans la forme d’une forme d’onde, mais la limite disponible avant que le bruit numérique n’interfère avec notre signal.
Il y a pas mal de choses à vérifier dans l’exemple ci-dessous, donc d’abord une explication rapide de ce que nous regardons. Nous avons nos formes d’onde d’entrée (bleu) et quantifiées (orange) dans les graphiques supérieurs, avec des profondeurs de bits de 2, 4 et 8 bits. Nous avons également ajouté une petite quantité de bruit à notre signal pour mieux simuler le monde réel. En bas, nous avons un graphique de l’erreur de quantification ou du bruit d’arrondi, qui est calculé en soustrayant le signal quantifié du signal d’entrée.

Le bruit de quantification augmente plus la profondeur de bit est petite, à cause des erreurs d’arrondi.
En augmentant la profondeur de bit, le signal quantifié correspond clairement mieux au signal d’entrée. Cependant ce n’est pas ce qui est important, observez le signal d’erreur/bruit beaucoup plus important pour les profondeurs de bit inférieures. Le signal quantifié n’a pas supprimé les données de notre entrée, il a en fait ajouté ce signal d’erreur. La synthèse additive nous dit qu’un signal peut être reproduit par la somme de deux autres signaux quelconques, y compris les signaux déphasés qui agissent comme une soustraction. C’est ainsi que fonctionne l’annulation du bruit. Donc ces erreurs d’arrondi introduisent un nouveau signal de bruit.
Ce n’est pas seulement théorique, vous pouvez réellement entendre de plus en plus de bruit dans les fichiers audio à faible profondeur de bits. Pour comprendre pourquoi, examinez ce qui se passe dans l’exemple de 2 bits avec de très petits signaux, comme avant 0,2 seconde. Cliquez ici pour obtenir un graphique agrandi. De très petits changements dans le signal d’entrée produisent de grands changements dans la version quantifiée. C’est l’erreur d’arrondi en action, qui a pour effet d’amplifier le bruit des petits signaux. Donc, une fois de plus, le bruit devient plus fort à mesure que la profondeur de bit diminue.
La quantification ne supprime pas les données de notre entrée, elle ajoute en fait un signal d’erreur bruyant.
Pensez aussi à l’inverse : il n’est pas possible de capturer un signal plus petit que la taille du pas de quantification – ironiquement connu comme le bit le moins significatif. Les petites modifications du signal doivent sauter au niveau de quantification le plus proche. Les profondeurs de bits plus importantes ont des pas de quantification plus petits et donc des niveaux d’amplification du bruit plus petits.
Plus important encore cependant, notez que l’amplitude du bruit de quantification reste constante, quelle que soit l’amplitude des signaux d’entrée. Cela démontre que le bruit se produit à tous les différents niveaux de quantification, il y a donc un niveau de bruit constant pour toute profondeur de bit donnée. Des profondeurs binaires plus importantes produisent moins de bruit. Nous devrions donc considérer les différences entre les profondeurs de 16 et 24 bits non pas comme la précision de la forme d’une onde, mais comme la limite disponible avant que le bruit numérique n’interfère avec notre signal.
La profondeur de bits est une question de bruit
Maintenant que nous parlons de la profondeur de bits en termes de bruit, revenons une dernière fois à nos graphiques ci-dessus. Notez comment l’exemple 8 bits semble correspondre presque parfaitement à notre signal d’entrée bruyant. Cela est dû au fait que sa résolution de 8 bits est en fait suffisante pour capturer le niveau du bruit de fond. En d’autres termes : la taille du pas de quantification est inférieure à l’amplitude du bruit, ou le rapport signal/bruit (SNR) est meilleur que le niveau du bruit de fond.
L’équation 20log(2n), où n est la profondeur de bit, nous donne le SNR. Un signal de 8 bits a un SNR de 48dB, 12-bits est 72dB, tandis que 16-bit atteint 96dB, et 24-bits un énorme 144dB. C’est important car nous savons maintenant que nous n’avons besoin que d’une profondeur de bit avec un SNR suffisant pour accommoder la gamme dynamique entre notre bruit de fond et le signal le plus fort que nous voulons capturer pour reproduire l’audio aussi parfaitement qu’il apparaît dans le monde réel. Cela devient un peu délicat de passer des échelles relatives du domaine numérique aux échelles basées sur la pression acoustique du monde physique, nous allons donc essayer de rester simples.
Nous avons besoin d’une profondeur de bits avec un SNR suffisant pour tenir compte de notre bruit de fond afin de capturer notre audio aussi parfaitement qu’il apparaît dans le monde réel.
Votre oreille a une sensibilité allant de 0dB (silence) à environ 120dB (son douloureusement fort), et la capacité typique à discerner les volumes est juste à 1dB d’écart. La gamme dynamique de votre oreille est donc d’environ 120dB, soit près de 20 bits.
Cependant, vous ne pouvez pas entendre tout cela en même temps, car la membrane tympanique, ou tympan, se resserre pour réduire la quantité de volume atteignant réellement l’oreille interne dans les environnements bruyants. Vous n’allez pas non plus écouter de la musique à un niveau aussi élevé, sous peine de devenir sourd. En outre, les environnements dans lesquels vous et moi écoutons de la musique ne sont pas aussi silencieux que des oreilles saines peuvent l’entendre. Un studio d’enregistrement bien traité peut nous faire descendre en dessous de 20dB pour le bruit de fond, mais écouter dans un salon animé ou dans le bus va évidemment aggraver les conditions et réduire notre besoin d’une gamme dynamique élevée.
L’oreille humaine a une gamme dynamique énorme, mais juste pas tout en même temps. Le masquage et les protections auditives réduisent son efficacité.
En plus de tout cela : lorsque le volume sonore augmente, le masquage des fréquences plus élevées prend effet dans votre oreille. A des volumes faibles de 20 à 40dB, le masquage ne se produit pas sauf pour les sons proches en hauteur. Cependant, à 80 dB, les sons inférieurs à 40 dB sont masqués, tandis qu’à 100 dB, les sons inférieurs à 70 dB sont impossibles à entendre. La nature dynamique de l’oreille et du matériel d’écoute fait qu’il est difficile de donner un chiffre précis, mais la gamme dynamique réelle de votre audition est probablement de l’ordre de 70 dB dans un environnement moyen, et peut descendre jusqu’à 40 dB dans des environnements très forts. Une profondeur de bit de seulement 12 bits couvrirait probablement la plupart des gens, donc les CD 16 bits nous donnent beaucoup de marge de manœuvre.

hyperphysique Le masquage haute fréquence se produit à des volumes d’écoute élevés, limitant notre perception des sons plus faibles.
La plupart des instruments et des microphones d’enregistrement introduisent également du bruit (en particulier les amplis de guitare), même dans des studios d’enregistrement très silencieux. Il y a également eu quelques études sur la gamme dynamique de différents genres, dont celle-ci qui montre une gamme dynamique typique de 60dB. Sans surprise, les genres ayant une plus grande affinité avec les parties calmes, comme le chœur, l’opéra et le piano, présentent des gammes dynamiques maximales autour de 70 dB, tandis que les genres rock, pop et rap plus « forts » tendent vers 60 dB et moins. En fin de compte, la musique n’est produite et enregistrée qu’avec une certaine fidélité.
Vous connaissez peut-être aussi les « guerres du volume » de l’industrie musicale, qui vont certainement à l’encontre de l’objectif des formats audio Hi-Res actuels. L’utilisation intensive de la compression (qui renforce le bruit et atténue les pics) réduit la plage dynamique. La musique moderne a une gamme dynamique considérablement réduite par rapport aux albums d’il y a 30 ans. En théorie, la musique moderne pourrait être distribuée à des débits binaires inférieurs à ceux de la musique ancienne. Vous pouvez vérifier la gamme dynamique d’une gamme de nombreux albums ici.

La qualité des CD peut être « seulement » de 16 bits, mais c’est exagéré pour la qualité.
16 bits est tout ce dont vous avez besoin
Ce fut tout un voyage, mais nous espérons que vous êtes repartis avec une image beaucoup plus nuancée de la profondeur de bits, du bruit et de la gamme dynamique, que ces exemples trompeurs en escalier que vous voyez si souvent.
La profondeur de bits concerne le bruit, et plus vous avez de bits de données pour stocker l’audio : moins le bruit de quantification sera introduit dans votre enregistrement. Par la même occasion, vous serez également en mesure de capturer des signaux plus petits avec plus de précision, ce qui contribuera à faire passer le plancher de bruit numérique sous l’environnement d’enregistrement ou d’écoute. C’est la seule raison pour laquelle nous avons besoin de la profondeur de bits. Il n’y a aucun avantage à utiliser des profondeurs de bits énormes pour les masters audio.
Surprenant, 12 bits sont probablement suffisants pour un master musical au son décent et pour répondre à la gamme dynamique de la plupart des environnements d’écoute. Cependant, l’audio numérique transporte plus que de la musique, et des exemples comme la parole ou les enregistrements environnementaux pour la télévision peuvent utiliser une gamme dynamique plus large que la plupart de la musique. De plus, un peu de marge pour la séparation entre le fort et le faible n’a jamais fait de mal à personne.
Dans l’ensemble, 16 bits (96dB de plage dynamique ou 120dB avec le tramage appliqué) s’adaptent à une large gamme de types d’audio, ainsi qu’aux limites de l’audition humaine et des environnements d’écoute typiques. Les améliorations perceptives de la qualité 24 bits sont très discutables, si ce n’est un simple placebo, comme j’espère l’avoir démontré. De plus, l’augmentation de la taille des fichiers et de la bande passante les rend inutiles. Le type de compression utilisé pour réduire la taille du fichier de votre bibliothèque musicale ou de votre flux a un impact beaucoup plus perceptible sur la qualité du son que le fait qu’il s’agisse d’un fichier 16 ou 24 bits.