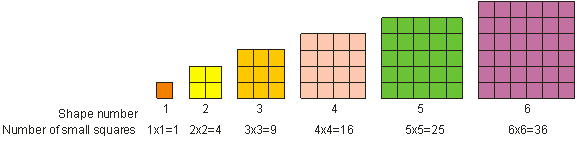Ymmärtäminen eksponenttien ja neliöjuurien
Oppimistavoite(t)
– Arvioi eksponentteja sisältäviä lausekkeita.
– Kirjoittaa toistuvia kertolaskuja käyttäen eksponenttimerkintää.
– Löytää täydellisen neliön neliöjuuren.
Esittely
Eksponentit tarjoavat erityisen tavan kirjoittaa toistuvia kertolaskuja. Tällä tavalla kirjoitetuilla luvuilla on erityinen muoto, jossa jokainen osa antaa tärkeää tietoa luvusta. Lukujen kirjoittaminen eksponenttien avulla voi myös säästää paljon tilaa. Luvun itsensä kanssa kertomisen käänteisoperaatiota kutsutaan luvun neliöjuuren löytämiseksi. Tämä operaatio on hyödyllinen neliön pinta-alaa koskevissa ongelmissa.
Eksponentiaalisen merkintätavan ymmärtäminen
Eksponentiaalinen merkintätapa on erityinen tapa kirjoittaa toistuvia tekijöitä, esimerkiksi 7 – 7. Eksponentiaalisessa merkintätavassa on kaksi osaa. Merkintätavan toista osaa kutsutaan perusluvuksi. Perus on luku, joka kerrotaan itsellään. Toinen osa on eksponentti eli potenssi. Tämä on pieni luku, joka on kirjoitettu korkealle perusluvun oikealle puolelle. Eksponentti eli potenssi kertoo, kuinka monta kertaa peruslukua käytetään kertolaskussa tekijänä. Esimerkissä 7 – 7 voidaan kirjoittaa 72:ksi, 7 on perusta ja 2 on eksponentti. Eksponentti 2 tarkoittaa, että tekijöitä on kaksi.
72 = 7 – 7 = 49
Voit lukea 72:n ”seitsemänä neliö”. Tämä johtuu siitä, että luvun kertomista itsellään kutsutaan ”luvun neliöimiseksi”. Vastaavasti luvun korottamista potenssiin 3 kutsutaan ”luvun kuutioimiseksi”. Voit lukea 73:n ”seitsemänä kuutioituna.”
Voit lukea 25:n ”kahtena viidenteen potenssiin” tai ”kahtena viiden potenssiin”. Voit lukea 84 ”kahdeksan neljänteen potenssiin” tai ”kahdeksan neljän potenssiin”. Tätä muotoa voidaan käyttää minkä tahansa eksponentiaalimuodossa kirjoitetun luvun lukemiseen. Itse asiassa, vaikka 63 luetaan tavallisimmin ”kuusi kuutioina”, se voidaan lukea myös ”kuusi kolmanteen potenssiin” tai ”kuusi potenssiin kolme.”
Kirjoittaaksesi eksponentiaalimuodossa kirjoitetun luvun arvon, kirjoita luku uudelleen toistuvaksi kertolaskuksi ja suorita kertolasku. Alla on kaksi esimerkkiä.
|
Esimerkki |
||||
|
Tehtävä |
Löydä luvun 42 arvo. |
|||
|
4 on perusta. 2 on eksponentti. |
Eksponentti tarkoittaa toistuvaa kertolaskua. Perus on 4; 4 on luku, joka kerrotaan. Eksponentti on 2; Tämä tarkoittaa, että käytetään kertolaskussa kahta 4:n tekijää. |
|||
|
42 = 4 – 4 |
Kirjoitetaan uudelleen toistettuna kertolaskuna. |
|||
|
4 – 4 = 16 |
Kertaa. |
|||
|
Vastaus 42 = 16 |
||||
|
Esimerkki |
||||
|
Ongelma |
Löydä arvo 25. |
|||
|
2 – 2 – 2 – 2 – 2 – 2 |
Kirjoita 25 uudelleen toistettuna kertolaskuna. Perusluku on 2, luku, joka kerrotaan. Eksponentti on 5, montako kertaa 2 käytetään kertolaskussa. |
|||
|
2 – 2 – 2 – 2 – 2 – 2 4 – 2 – 2 – 2 – 2 8 – 2 – 2 16 – 2 32 |
Toteuta kertolasku. |
|||
|
Vastaus 25 = 32 |
||||
Löydä 43:n arvo.
A) 12
B) 64
C) 256
D) 43
Kertauskertolaskun kirjoittaminen eksponenttien avulla
Kertauskertolaskun kirjoittaminen eksponenttimuodossa voi säästää aikaa ja tilaa. Tarkastellaan esimerkkiä 5 – 5 – 5 – 5 – 5. Voimme käyttää eksponenttimerkintää kirjoittaaksemme tämän toistetun kertolaskun muodossa 54. Koska 5 kerrotaan, se kirjoitetaan peruslukuna. Koska peruslukua käytetään kertolaskussa neljä kertaa, eksponentti on 4. Lauseke 5 – 5 – 5 – 5 – 5 voidaan kirjoittaa lyhyesti eksponentiaalisella merkintätavalla muotoon 54, ja se kuuluu seuraavasti: ”viisi neljänteen potenssiin” tai ”viisi potenssiin 4.”
Kirjoittaaksesi saman luvun toistuvan kertolaskun eksponentiaalisella merkintätavalla, kirjoita aluksi kerrottava luku peruslukuna. Laske sitten, kuinka monta kertaa kyseistä lukua käytetään kertolaskussa, ja kirjoita tämä luku eksponentiksi. Muista laskea luvut, älä kertolaskun merkkejä, eksponentin määrittämiseksi.
|
Esimerkki |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Tehtävä |
Kirjoita 7 – 7 – 7 eksponenttimerkinnällä. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7 on perusta.
Koska 7:ää käytetään kolme kertaa, 3 on eksponentti. |
Perusluku on luku, joka kerrotaan, eli 7. Eksponentti kertoo, kuinka monta kertaa perusluku kerrotaan. A) 1 000 000 B) 60 C) 105 D) 106 Näytä/piilota vastaus
Neliöjuurien ymmärtäminen ja laskeminen Kuten aiemmin huomasit, 52:ta kutsutaan ”viideksi neliöksi”. ”Viisi neliössä” tarkoittaa, että kerrotaan viisi itsellään. Matematiikassa kutsumme luvun kertomista itsellään luvun neliöimiseksi. Kutsumme kokonaisluvun neliöimisen tulosta neliöksi tai täydelliseksi neliöksi. Täydellinen neliö on mikä tahansa luku, joka voidaan kirjoittaa kokonaislukuna potenssiin 2. Esimerkiksi 9 on täydellinen neliö. Täydellinen neliöluku voidaan esittää neliön muotoisena, kuten alla on esitetty. Näemme, että 1, 4, 9, 16, 25 ja 36 ovat esimerkkejä täydellisistä neliöistä.
Luvun neliöimiseksi luku kerrotaan itsellään. 3 neliössä = 32 = 3 – 3 = 9. Alhaalla on lisää esimerkkejä täydellisistä neliöistä.
Luvun neliöimisen käänteisoperaatiota kutsutaan luvun neliöjuuren löytämiseksi. Neliöjuuren etsiminen on kuin kysyisi: ”Mikä luku kerrottuna itsellään antaa minulle tämän luvun?”. 25:n neliöjuuri on 5, koska 5 kerrottuna itsellään on 25. Neliöjuuret kirjoitetaan matemaattisella symbolilla, jota kutsutaan radikaalimerkiksi ja joka näyttää tältä:
Löydä A) 6 B) 18 C) 72 D) 7 Näytä/piilota vastaus
Yhteenveto Eksponentiaalinen merkintätapa on lyhennetty tapa kirjoittaa saman luvun toistuva kertominen. Eksponenttimerkinnällä kirjoitetussa luvussa on perusta ja eksponentti, ja kumpikin näistä osista antaa tietoa lausekkeen arvon löytämiseksi. Perusosa kertoo, mikä luku kerrotaan toistuvasti, ja eksponentti kertoo, kuinka monta kertaa perusosaa käytetään kertolaskussa. Eksponenteilla 2 ja 3 on erikoisnimet. Perusteen korottamista potenssiin 2 kutsutaan luvun neliöimiseksi. Perusluvun korottamista potenssiin 3 kutsutaan luvun ”kuutioimiseksi”. Luvun neliöimisen käänteisluku on luvun neliöjuuren löytäminen. Jos haluat löytää luvun neliöjuuren, kysy itseltäsi: ”Minkä luvun voin kertoa itsellään saadakseni tämän luvun?” |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||