Tällä oppitunnilla näytämme helpon strategian seuraavan ongelman ratkaisemiseksi: miten löytää tasakylkisen kolmion pinta-ala.
Käytetään käytännössä joitakin tähän mennessä todistamiamme ominaisuuksia seuraavassa geometriaongelmassa:
Ongelma
Tässä tasakylkisessä kolmiossa ΔABC, jonka jalan pituus on 10, on korkeus tyvestä yhtä suuri kuin kaksi kolmasosaa tyvestä. Etsi kolmion pinta-ala.
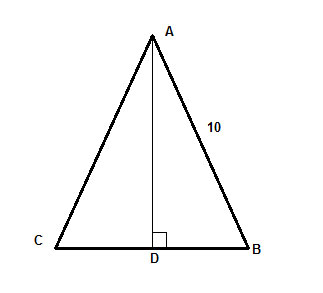
Strategia
Ratkaistaksemme tämän ongelman, Työskentelemme takaperin siitä, mitä meidän täytyy tehdä.
Meidän täytyy löytää kolmion pinta-ala, jonka tiedämme saatavan kaavalla (pohja kertaa korkeus)/2.
Esimerkkinä ongelmastamme on se, että emme tiedä sen enempää tyven pituutta kuin korkeutta. Mutta meille annetaan niiden välinen suhde, joka on vihje siitä, mitä meidän on tehtävä. Kutsutaan pohjan, BC, pituutta x:ksi.
Tiedämme sitten, että korkeus, AD, on 2x/3, kuten tehtävässä annetaan.
Etsimämme vastaus on siis (pohja kertaa korkeus)/2 eli x kertaa 2x/3 jaettuna kahdella.
Mutta miten löydämme x:n? On kaksi ylimääräistä asiaa, jotka meille annettiin tehtävässä ja joita emme ole vielä käyttäneet – jalan pituus (10) ja se, että kyseessä on tasakylkinen kolmio. Meidän on luultavasti käytettävä näitä kahta asiaa ratkaistaksemme ongelman.
Katsotaan vielä kerran tasakylkisten kolmioiden ominaisuuksia. Yksi asia, joka tulisi heti mieleen, on se, että kuten olemme osoittaneet, tasakylkisessä kolmiossa korkeus tyvestä puolittaa tyven, joten CD=DB=x/2.
Loppujen lopuksi AD on korkeus, mikä tarkoittaa, että kulma ∠ADC on suorakulma, ja meillä on suorakulmainen kolmio ΔADC, jonka hypotenuusan tiedämme (10) ja jonka avulla voimme löytää jalat Pythagoraan lauseen avulla, c2 =a2+b2,
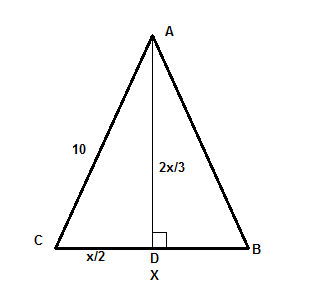
jossa c=10 ,a=x/2 ja b=2x/3 . Ja olemme valmiit, loppu on vain x:n algebrallinen ratkaiseminen.
Todistus: Tasakylkisen kolmion pinta-ala
(1) ΔADC on suorakulmainen kolmio //given, koska AD on korkeus tyvestä
(2) AC2 =CD2 + AD2 //Pythagoraan lause
(3) AC= 10 //myös
(4) CB = x
(5) CD = x/2 //Korkeus tyvestä tasakylkisessä kolmiossa puolittaa tyven
(6) AD = 2x/3 //edelleen
(7) 102 = (x/2)2 + (2x/3)2 //Substituoidaan (2)
(8) 100 = x2/4+4×2/9 //yksinkertaistetaan
(9) 100*36 = 9×2 +16×2 //kummatkin puolet kerrotaan 36:lla
(10) 100*36 = 25×2 //kerätään samankaltaisia termejä