
Politiikan kysymys: Hybridiauton hankintaverohyvitys – Onko se hallituksen paras valinta polttoaineen kulutuksen ja hiilidioksidipäästöjen vähentämiseksi?
Yhdysvaltalaiset ja hallitus ovat huolissaan riippuvuudesta ulkomaisesta tuontiöljystä ja hiilidioksidipäästöistä ilmakehään. Vuonna 2005 kongressi hyväksyi lain, jolla kuluttajille myönnettiin verohyvityksiä sähkö- ja hybridiautojen hankintaan.
Tämä verohyvitys voi vaikuttaa hyvältä poliittiselta valinnalta, mutta se on kallis, koska se pienentää suoraan Yhdysvaltain hallituksen keräämien tulojen määrää. Onko olemassa tehokkaampia lähestymistapoja vähentää riippuvuutta fossiilisista polttoaineista ja hiilidioksidipäästöjä? Miten päätämme, mikä politiikka on parasta? Vastataksemme tähän kysymykseen poliittisten päättäjien on ennustettava jollakin tarkkuudella, miten kuluttajat reagoivat tähän veropolitiikkaan, ennen kuin nämä päättäjät käyttävät miljoonia liittovaltion dollareita.
Voidaan soveltaa hyödyllisyyden käsitettä tähän poliittiseen kysymykseen. Tässä moduulissa tutkimme hyötyjä ja hyötyfunktioita. Sen jälkeen pystymme käyttämään sopivaa hyötyfunktiota päättelemään välinpitämättömyyskäyriä, jotka kuvaavat poliittista kysymystämme.
Poliittisen kysymyksen tutkiminen
Asettakaamme, että hybridiautojen ostojen tukemiseen tarkoitettu verohyvitys on hurjan menestyksekäs ja että se kaksinkertaistaa kaikkien Yhdysvaltain teillä liikkuvien autojen keskimääräisen polttoainetaloudellisuuden – tulos, joka ei selvästikään ole realistinen, mutta joka on hyödyllinen myöhempien keskustelujemme kannalta. Mitä mielestänne tapahtuisi kaikkien yhdysvaltalaisten autoilijoiden polttoaineenkulutukselle? Pitäisikö hallituksen odottaa, että autojen polttoaineenkulutus ja hiilidioksidipäästöt puolittuisivat vastauksena tähän? Miksi vai miksi ei?
2.1 Hyötyfunktiot
LO 2.1: Kuvaile hyötyfunktio.
2.2 Hyötyfunktiot ja tyypilliset preferenssit
LO 2.2: Tunnista hyötyfunktiot niiden edustamien tyypillisten preferenssien perusteella.
2.3 Hyötyfunktioiden ja indifferenssikäyräkarttojen suhteuttaminen
LO 2.3: Selitä, miten hyötyfunktiosta johdetaan indifferenssikäyrä.
2.4 Marginaalihyödyn ja marginaalisen substituutiovauhdin löytäminen
LO 2.4: Johdetaan marginaalihyöty ja MRS tyypillisille hyötyfunktioille.
2.5. Politiikkakysymys
2.1 Hyötyfunktiot
LO1: Kuvaile hyötyfunktio.
Preferenssiemme avulla voimme tehdä vertailuja eri kulutusnippujen välillä ja valita mieluisimmat. Voimme esimerkiksi määrittää kokonaisen nippujen joukon paremmuusjärjestyksen mieltymyksiemme perusteella. Hyötyfunktio on matemaattinen funktio, joka asettaa kulutushyödykkeiden niput paremmuusjärjestykseen antamalla kullekin nipulle numeron, jossa suuremmat numerot merkitsevät mieluisampia nippuja. Hyötyfunktioilla on samat ominaisuudet kuin moduulissa 1 määritellyillä preferensseillä. Toisin sanoen: ne pystyvät järjestämään nippuja, ne ovat täydellisiä ja transitiivisia, enemmän on parempi kuin vähemmän, ja asiaankuuluvissa tapauksissa sekaniput ovat parempia.
Lukua, jonka hyötyfunktio antaa tietylle nipulle, kutsutaan hyötyarvoksi, eli tyydytykseksi, jonka kuluttaja saa tietystä nipusta. Kullekin nipulle annettu hyötyluku ei tarkoita absoluuttisesti mitään; ei ole olemassa mitään yhtenäistä asteikkoa, jota vasten tyytyväisyyttä mitattaisiin. Sen ainoa merkitys on suhteellisessa mielessä: hyödyn avulla voimme määrittää, mitkä niput ovat parempia kuin toiset.
Jos nipusta A saatava hyöty on suurempi kuin nipusta B saatava hyöty, se vastaa sitä, että kuluttaja pitää nipusta A parempana kuin nipusta B. Hyötyfunktiot asettavat siis kuluttajien mieltymykset paremmuusjärjestykseen antamalla kullekin nipulle numeron. . Voimme käyttää hyötyfunktiota moduulissa 1 kuvattujen indifferenssikäyräkarttojen piirtämiseen. Koska kaikki samalla indifferenssikäyrällä olevat niput tuottavat saman tyydytyksen, eikä yksikään niistä siis ole mieluisin, jokaisella nipulla on sama hyöty. Voimme siis piirtää indifferenssikäyrän määrittämällä kaikki ne niput, jotka tuottavat saman luvun hyötyfunktiosta.
Taloustieteilijät sanovat, että hyötyfunktiot ovat pikemminkin ordinaalisia kuin kardinaalisia. Ordinaalinen tarkoittaa, että hyötyfunktiot vain järjestävät niput paremmuusjärjestykseen – ne osoittavat vain, mikä niistä on parempi, eivät sitä, kuinka paljon parempi se on kuin toinen nippu. Oletetaan esimerkiksi, että yksi hyötyfunktio osoittaa, että nippu A tuottaa 10 hyödykettä ja nippu B 20 hyödykettä. Emme sano, että nippu B on kaksi kertaa niin hyvä tai 10 hyödykettä parempi, vaan ainoastaan, että kuluttaja pitää mieluummin nipusta B. Oletetaan esimerkiksi, että ystäväsi osallistuu kilpailuun ja kertoo sinulle tulleensa kolmanneksi. Tämä tieto on ordinaalinen: Tiedät, että hän oli nopeampi kuin neljänneksi sijoittunut ja hitaampi kuin toiseksi sijoittunut. Tiedät vain, missä järjestyksessä juoksijat sijoittuivat. Yksittäiset ajat ovat kardinaalisia: Koska hyötyfunktiot ovat ordinaalisia, monet eri hyötyfunktiot voivat edustaa samoja preferenssejä. Tämä pätee niin kauan kuin järjestys säilyy.
Tarvitaan esimerkiksi hyötyfunktio U, joka kuvaa preferenssejä yli hyödykkeiden A ja B nippujen: U(A,B). Voimme soveltaa tähän funktioon mitä tahansa positiivista monotonista muunnosta (mikä tarkoittaa lähinnä sitä, että emme muuta järjestystä), ja luomaamme uutta funktiota kuvaavat samat mieltymykset. Voimme esimerkiksi kertoa positiivisen vakion α tai lisätä positiivisen tai negatiivisen vakion β . Niinpä αU(A,B)+β edustaa täsmälleen samoja preferenssejä kuin U(A,B), koska se järjestää niput täsmälleen samalla tavalla. Tämä tosiasia on varsin hyödyllinen, koska joskus positiivisen monotonisen muunnoksen soveltaminen hyötyfunktioon helpottaa ongelmien ratkaisemista.
2.2 Hyötyfunktiot ja tyypilliset preferenssit
LO2: Tunnista hyötyfunktioita niiden edustamien tyypillisten preferenssien perusteella
Tarkastellaan omenanippuja A ja banaaninippuja B. Hyötyfunktio, joka kuvaa Isaacin preferenssejä omena- ja banaaninippuja kohtaan, on funktio U(A,B). Mutta mitkä ovat Isaacin erityiset mieltymykset omena- ja banaanipaketteja kohtaan? Oletetaan, että Isaacilla on melko tavanomaiset omenoita ja banaaneja koskevat mieltymykset, jotka johtavat tyypillisiin indifferenssikäyriimme: Hän suosii enemmän kuin vähemmän, ja hän pitää monipuolisuudesta. Näitä mieltymyksiä kuvaava hyötyfunktio voisi olla:
U(A,B) = AB
Jos omenat ja banaanit ovat Isaacin mieltymyksissä täydellisiä komplementteja, hyötyfunktio näyttäisi jotakuinkin tältä:
U(A,B) = MIN,
jossa MIN-funktio yksinkertaisesti antaa funktiolle pienemmän kahdesta luvusta.
Jos omenat ja banaanit ovat täydellisiä substituutteja, hyötyfunktio on additiivinen ja se näyttäisi jotakuinkin tältä:
U(A,B) = A + B
Hyötyfunktioiden luokka, joka tunnetaan nimellä Cobb-Douglas-hyötyfunktiot, on taloustieteessä hyvin yleisesti käytetty kahdesta syystä:
1. Ne edustavat ”hyvin käyttäytyviä” mieltymyksiä, kuten enemmän on parempi ja mieltymys monipuolisuuteen.
2. Ne ovat hyvin joustavia ja niitä voidaan mukauttaa hyvin helposti vastaamaan reaalimaailman tietoja.
Cobb-Douglas-hyötyfunktiot ovat seuraavassa muodossa:
U(A,B) = AαBβ
Koska positiiviset monotoniset muunnokset edustavat samoja preferenssejä, yhtä tällaista muunnosta voidaan käyttää asettamaan α + β = 1 , minkä tulemme myöhemmin huomaamaan, että se on kätevä ehto, joka yksinkertaistaa jonkin verran matemaattista laskutoimitusta kuluttajan valintatehtävässä.
Toinen tapa muuntaa hyötyfunktio hyödyllisellä tavalla on ottaa funktiosta luonnollinen logi, jolloin syntyy uusi funktio, joka näyttää tältä:
U(A,B) = αln(A) + βln(B)
Johdattaaksemme tämän yhtälön sovellamme yksinkertaisesti luonnollisen login sääntöjä . Tässä on tärkeää pitää mielessä abstraktiotaso. Emme yleensä voi tehdä erityisiä hyötyfunktioita, jotka kuvaisivat tarkasti yksilöllisiä mieltymyksiä. Todennäköisesti kukaan meistä ei pystyisi kuvaamaan omia mieltymyksiään yhdellä yhtälöllä. Mutta niin kauan kuin kuluttajien yleiset mieltymykset noudattavat perusoletuksiamme, voimme melko hyvin löytää hyötyfunktioita, jotka vastaavat todellisia kulutustietoja. Näemme tästä todisteita myöhemmin kurssilla.
Taulukossa 2.1 on yhteenveto tässä jaksossa kuvatuista preferensseistä ja hyötyfunktioista.
|
Taulukko 2. Kuluttajien preferenssit ja hyötyfunktiot.1 Preferenssien tyypit ja niitä edustavat hyötyfunktiot |
||
|
PREFERENSSIT |
UTILITYKSET FUNKTIO |
TYYPPI UTILITY FUNKTIO |
|
Monipuolisuuden rakkaus tai ”Hyvin käyttäytyvä” |
U(A,B) = AB |
Cobb-Douglas |
|
Monipuolisuusrakkaus tai ”hyvin käyttäytyvä” |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Monipuolisuusrakkaus tai ”hyvin käyttäytyvä” |
U(A,B) = αln(A) + βln(B) |
Luonnollinen log Cobb-Douglas |
|
Täydelliset komplementit |
U(A,B) = MIN |
Min-funktio |
|
Täydelliset korvaajat |
U(A,B) = A + B |
Additiivinen |
2.3 Hyötyfunktioiden ja indifferenssikäyräkarttojen suhteuttaminen
LO3: Selitä, miten hyötyfunktiosta johdetaan indifferenssikäyrä
Indifferenssikäyrät ja hyötyfunktiot liittyvät suoraan toisiinsa. Itse asiassa, koska indifferenssikäyrät esittävät preferenssejä graafisesti ja hyötyfunktiot matemaattisesti, seuraa siitä, että indifferenssikäyrät voidaan johtaa hyötyfunktioista.
Yksimuuttujaisissa funktioissa riippuvainen muuttuja piirretään pystyakselille ja riippumaton muuttuja vaaka-akselille, kuten kuvaaja y=f(x). Sen sijaan kaksimuuttujaisten funktioiden kuvaajat ovat kolmiulotteisia, kuten U=U(A,B). Kuvassa 2.1 on esitetty kuvaaja U=A^\frac{1}{2}B^\frac{1}{2}. Kolmiulotteiset kuvaajat ovat hyödyllisiä, kun halutaan ymmärtää, miten hyöty kasvaa sekä A:n että B:n kulutuksen kasvaessa.
Kuvio 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
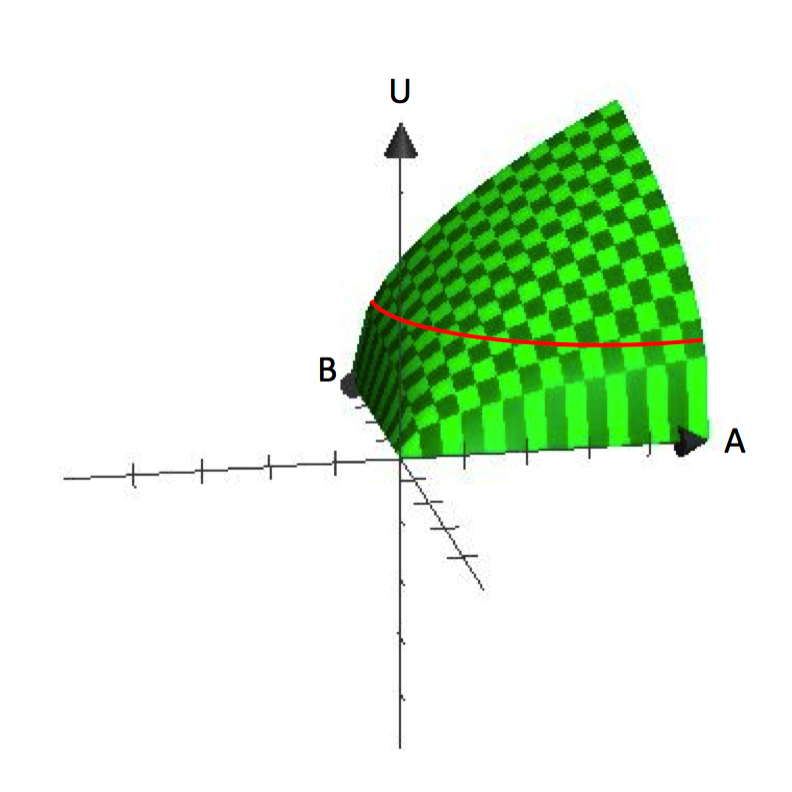
Kuviosta 2.1 käy selvästi ilmi olettamus, jonka mukaan kuluttajat suosivat monipuolisuutta. Jokainen nippu, joka sisältää tietyn määrän A:ta ja B:tä, edustaa pistettä pinnalla. Pinnan pystysuora korkeus edustaa hyödyn tasoa. Lisäämällä sekä A:ta että B:tä kuluttaja voi saavuttaa korkeampia pisteitä pinnalla.
Miten siis indifferenssikäyrät syntyvät? Muistutetaan, että välinpitämättömyyskäyrä on kokoelma kaikkia nippuja, joiden suhteen kuluttaja on välinpitämätön sen suhteen, mitä niistä kuluttaa. Matemaattisesti tämä vastaa sitä, että kaikki niput, kun ne asetetaan hyötyfunktioon, tuottavat saman funktionaalisen arvon. Jos siis asetamme hyödyllisyydelle arvon Ū ja etsimme kaikki niput A ja B, jotka tuottavat tämän arvon, määrittelemme välinpitämättömyyskäyrän. Huomaa, että tämä vastaa kaikkien niiden nippujen löytämistä, jotka saavat kuluttajan samalle korkeudelle kolmiulotteisella pinnalla kuvassa 2.1.
Ymmärryksettömyyskäyrät ovat korkeuden (hyötytason) esitys tasaisella pinnalla. Tällä tavoin ne ovat analogisia topografisen kartan korkeusviivojen kanssa. Viemällä kolmiulotteinen kuvaaja takaisin kaksiulotteiseen avaruuteen – A, B -avaruuteen – voimme näyttää ääriviivat/erokäyrät, jotka edustavat eri korkeuksia tai hyötytasoja. Kuvassa 2.1 olevasta kuvaajasta voi jo nähdä, miten tämä hyötyfunktio tuottaa indifferenssikäyrät, jotka ovat ”kaarevia” tai koveria origoon nähden.
Siten indifferenssikäyrät seuraavat suoraan hyötyfunktioista ja ovat käyttökelpoinen tapa esittää hyötyfunktioita kaksiulotteisessa kuvaajassa.
2.4 Rajahyödyn ja marginaalisubstituutionopeuden löytäminen
LO4: Johdetaan marginaalihyöty ja MRS tyypillisille hyötyfunktioille.
Marginaalihyöty on lisähyöty, jonka kuluttaja saa kuluttamalla yhden ylimääräisen hyödykkeen yksikön. Matemaattisesti tämä ilmaistaan seuraavasti:
MU_{a}=\frac{\Delta \cup }{\Delta A}
tai hyödyn muutos kulutetun A:n määrän muutoksesta johtuvasta hyödyn muutoksesta, jossa Δ edustaa hyödykkeen arvon muutosta. Eli,
MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Huomaa, että tarkastellessamme A:n kulutuksen rajahyötyä pidämme B:n vakiona.
Laskennan avulla rajahyöty on sama kuin hyötyfunktion osittaisderivaatta A:n suhteen:
MU_{A}\frac{\partial U(A,B)}{\partial A}
Asettele kuluttaja, joka istuu syömään aterian, jossa on salaattia ja pizzaa. Oletetaan, että pidämme salaatin määrän vakiona – esimerkiksi yksi lisukesalaatti illallisen kanssa. Nyt lisätään pizzaviipaleiden määrää Oletetaan, että 1viipaleella hyöty on 10, 2:lla 18, 3:lla 24 ja 4:llä 28. Piirretään nämä luvut kuvaajaan, jossa hyöty on pystyakselilla ja pizza vaaka-akselilla (kuva 2.2).
Kuva 2.2: Vähenevän rajahyödyn kuvaaja ja taulukko
|
Pizzaviipaleet |
Hyöty |
Marginaalinen Utility |
|
|
1 |
10 |
|
|
|
2 |
18 |
8 |
|
|
3 |
24 |
6 |
|
|
4 |
28 |
4 |
|
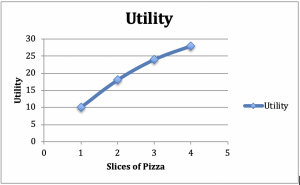
Kuvaajan positiivisesta kaltevuudesta, näemme, että pizzaviipaleiden lisäyksestä aiheutuva hyöty kasvaa. Kuvaajan koverasta muodosta näemme toisen yleisen ilmiön: Lisähyöty, jonka kuluttaja saa jokaisesta ylimääräisestä pizzaviipaleesta, pienenee kulutettujen viipaleiden määrän kasvaessa.
Tietoa siitä, että lisähyöty pienenee jokaisen ylimääräisen pizzaviipaleen myötä, kutsutaan pienenevän rajahyödyn periaatteeksi. Tämä periaate pätee hyvin käyttäytyviin preferensseihin, joissa suositaan sekapaketteja.
Marginaalinen korvattavuusaste (MRS) on se määrä yhtä tavaraa, josta kuluttaja on valmis luopumaan saadakseen yhden yksikön toista tavaraa. Siksi se on sama asia kuin välinpitämättömyyskäyrän kaltevuus – koska pidämme tyytyväisyystason vakiona, pysymme samalla välinpitämättömyyskäyrällä, siirrymme vain sitä pitkin vaihtaessamme yhtä tavaraa toiseen. Se, kuinka paljon olet valmis vaihtamaan yhdestä hyödystä toiseen, riippuu kunkin hyödyn rajahyödystä.
Käyttäen edellistä esimerkkiämme, jos kuluttamalla yhden lisäsalaatin sivusalaatin hyötysi nousee 10:llä, voisit luopua kahdesta pizzaviipaleesta, kun kulutat tällä hetkellä 4 viipaletta pizzaa, ja siirtyä 28:sta 18:aan hyötyyn. Salaatista saatava 10 lisähyötyä ja kahdesta pizzaviipaleesta luopuminen vähentää hyötyjä 10:llä, joten kokonaishyöty pysyy muuttumattomana, joten meidän on edelleen oltava samalla välinpitämättömyyskäyrällä. Kun liikumme indifferenssikäyrää pitkin, meidän on ratsastettava kaltevuudella, eli meidän on luovuttava pystyakselilla olevasta hyödykkeestä vaaka-akselilla olevan hyödykkeen lisäämiseksi, mikä johtaa negatiiviseen nousuun positiivisen juoksun aikana.
Voimme siirtyä suoraan marginaalihyötysuhteesta MRS:ään tunnistamalla näiden kahden käsitteen välisen yhteyden. Tapauksessamme hyötyfunktiolle U=U(A,B) , MRS esitetään seuraavasti:
MRS=-\frac{MU_{A}}{MU_{B}}
Huomaa, että korvaamalla voimme yksinkertaistaa yhtälöä:
MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{\frac{\frac{\Delta U}{\Delta A}}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}
Sisällyttämällä laskutoimituksen se vastaa:
MRS=-\frac{\frac{\partial U(A,B)}{\partial A}}{\frac{\partial U(A,B)}{\partial B}}
2.5 Politiikkakysymys
Moduulissa 1 totesimme, että relevantti kuluttajan päätös enemmän ajettujen kilometrien ja muun kulutuksen välillä on todennäköisesti kuluttajien valintaa koskevien vakio-oletusten mukainen. Siksi on hyvä valinta käyttää Cobb-Douglas-hyötyfunktiota kuvaamaan kuluttajaa, joka haluaa ajaa autolla sekä kuluttaa muita kulutushyödykkeitä ja joka näkee ne kompromissina (bensiiniin käytetty raha on rahaa, jota ei käytetä muihin kulutushyödykkeisiin). Sillä on myös se etu, että se sekä vastaa oletuksia että on joustava:
U(MD,C)=MD^{a}C^{\beta } ,
jossa MD = ajetut kilometrit ja C = muu kulutus.
Itse asiassa itse funktio voidaan viedä reaalimaailman aineistoon, jossa parametrit ja voidaan estimoida tälle markkinalle, kuluttajan autolla ajettujen kilometrien markkinalle.
Kuvio 2.3 Politiikkaesimerkin indifferenssikäyrien kuvaaja
Poliittisten kysymyksien pohdinta:
1 . Olisivatko muut preferenssityypit sopivampia tässä esimerkissä?
2. Minkä pitäisi olla totta, jotta täydelliset komplementit olisivat sopiva preferenssityyppi tämän politiikan analysoimiseksi?
Minkä pitäisi olla totta täydellisille substituuteille? Koska tarkastelemme ”tyypillistä” kuluttajaa, joka ajaa autoa, onko tarkoituksenmukaista valita ”tyypillinen” hyötyfunktio?
4. Arvaammeko vain, vai onko meillä teoriapohjaa, joka tukee valintamme ”hyvin käyttäytyvistä” preferensseistä tai Cobb-Douglas-hyötyfunktiosta?
YHTEENVETO
Katsaus: Aiheet ja niihin liittyvät oppimistulokset
2.1 Hyötyfunktiot
LO 2.1: Kuvaile hyötyfunktio
2.2 Hyötyfunktiot ja tyypilliset preferenssit
LO 2.2: Tunnista hyötyfunktiot niiden edustamien tyypillisten preferenssien perusteella
2.3 Hyötyfunktioiden ja indifferenssikäyräkarttojen suhteuttaminen
LO 2.3: Selitä, miten hyötyfunktiosta johdetaan indifferenssikäyrä
2.4 Rajahyödyn ja marginaalisen substituutiovauhdin löytäminen
LO 2.4: Johdetaan rajahyöty- ja marginaalihyötykäyräkartat tyypillisiä hyötyfunktioita varten
2.5. Policy Question
Learn: Keskeiset termit ja kuvaajat
Bi-…variate functions
Cardinal
Contour line
Diminishing marginal utility
Function
Marginal rate of substitution (MRS)
Marginal utility
Marginal utility
Ordinaalinen
Yksilukuiset funktiot
Hyöty
Hyötyfunktio
Hyötyfunktio
Graafit
3D-hyötyfunktio ja ääriviiva
Yhtälöt
Cobb-Douglas
Täydelliset komplementit
Täydelliset substituutit