Keskihajonta on keskimääräisen vaihtelun määrä aineistossasi. Se kertoo, kuinka kaukana kukin arvo keskimäärin on keskiarvosta.
Suuri keskihajonta tarkoittaa, että arvot ovat yleensä kaukana keskiarvosta, kun taas pieni keskihajonta osoittaa, että arvot ovat keskittyneet lähelle keskiarvoa.
Mitä keskihajonta kertoo?
Keskihajonta on hyödyllinen hajonnan mittari normaaleille jakaumille.
Normaaleissa jakaumissa aineisto jakaantuu symmetrisesti ilman vinoutta. Useimmat arvot ryhmittyvät keskialueen ympärille, ja arvot kapenevat, kun ne etääntyvät kauemmas keskipisteestä. Keskihajonta kertoo, kuinka kaukana jakauman keskipisteestä datasi keskimäärin on.
Monet tieteelliset muuttujat noudattavat normaalijakaumia, kuten pituus, standardoidut testitulokset tai työtyytyväisyysarviot. Kun sinulla on eri otosten keskihajonnat, voit vertailla niiden jakaumia tilastollisten testien avulla ja tehdä päätelmiä suuremmista populaatioista, joista ne ovat peräisin.
Keskiarvot (M) ovat samat jokaisessa ryhmässä – se on x-akselilla oleva arvo, kun käyrä on huipussaan. Niiden keskihajonnat (SD) poikkeavat kuitenkin toisistaan.
Keskihajonta kuvastaa jakauman hajontaa. Käyrällä, jolla on pienin keskihajonta, on korkea huippu ja pieni hajonta, kun taas käyrä, jolla on suurin keskihajonta, on tasaisempi ja laajemmalle levinnyt.
Empiirinen sääntö
Keskiarvo ja keskihajonta yhdessä kertovat, missä useimmat jakauman arvot sijaitsevat, jos jakauma noudattaa normaalijakaumaa.
Empiirinen sääntö eli 68-95-99,7-sääntö kertoo sinulle, missä arvosi sijaitsevat:
- Ympäri 68 % pistemääristä on kahden keskihajonnan sisällä keskiarvosta,
- Yli 95 % pistemääristä on neljän keskihajonnan sisällä keskiarvosta,
- Yli 99.7 % pisteistä on 6 keskihajonnan sisällä keskiarvosta.
Seurataan empiiristä sääntöä:
- Pistemääristä noin 68 % on välillä 40-60.
- Pistemääristä noin 95 % on välillä 30-70.
- Ympäri 99,7 % pisteistä on välillä 20-80.
Empiirinen sääntö on nopea tapa saada yleiskuva tiedoistasi ja tarkastaa mahdolliset poikkeamat tai ääriarvot, jotka eivät noudata tätä kaavaa.
Ei-normaaleille jakaumille keskihajonta on vähemmän luotettava vaihtelun mittari, ja sitä tulisi käyttää yhdessä muiden mittareiden, kuten vaihteluvälin tai interkvartiilialueen, kanssa.
Keskihajonnan kaavat populaatioille ja otoksille
Keskihajontojen laskemiseen käytetään erilaisia kaavoja riippuen siitä, onko kyseessä koko populaatiosta vai otoksesta saatu tieto.
Populaation keskihajonta
Kun olet kerännyt tiedot jokaiselta sinua kiinnostavan populaation jäseneltä, voit saada populaation keskihajonnalle tarkan arvon.
Populaation keskihajonnan kaava näyttää tältä:
| kaava | selitys |
|---|---|
 |
|
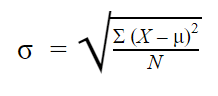Otoksen keskihajonta
Kun kerätään aineistoa otoksesta, otoksen keskihajontaa käytetään estimaattien tai johtopäätösten tekemiseen populaation keskihajonnasta.
Otoksen keskihajonnan kaava näyttää tältä:
| kaava | selitys |
|---|---|
 |
|
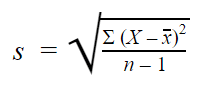Otoksilla käytämme kaavassa n – 1:tä, koska n:n käyttäminen antaisi vääristyneen estimaatin, joka johdonmukaisesti aliarvioisi vaihtelua. Otoksen keskihajonta olisi yleensä pienempi kuin populaation todellinen keskihajonta.
Vähentämällä otoksen n arvoksi n – 1 saadaan keskihajonnasta keinotekoisen suuri, jolloin saadaan varovainen estimaatti vaihtelusta.
Vaikka tämä ei ole puolueeton estimaatti, se on vähemmän puolueellinen estimaatti keskihajonnalle: on parempi yliarvioida kuin aliarvioida otosten vaihtelua.
Vaiheet keskihajonnan laskemiseksi
Keskihajonta lasketaan yleensä automaattisesti siinä ohjelmistossa, jota käytät tilastolliseen analyysiin. Voit kuitenkin laskea sen myös käsin, jotta ymmärrät paremmin, miten kaava toimii.
Keskihajonnan löytämiseen käsin on kuusi päävaihetta. Käytämme pientä 6 pisteen aineistoa käydessämme vaiheet läpi.
| Datajoukko | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Vaihe 1: Etsi keskiarvo
Keskiarvon löytämiseksi laske kaikki pisteet yhteen ja jaa ne sitten pisteiden lukumäärällä.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Vaihe 2: Etsitään kunkin pistemäärän poikkeama keskiarvosta
Vähennä keskiarvo jokaisesta pistemäärästä, jotta saat poikkeamat keskiarvosta.
Koska x̅ = 50, tässä vähennetään 50 jokaisesta pistemäärästä.
| Pisteet | Poikkeama keskiarvosta |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Vaihe 3: Neliöi jokainen poikkeama keskiarvosta
Kerro jokainen poikkeama keskiarvosta itsellään. Näin saadaan positiivisia lukuja.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Vaihe 4: Etsi neliöiden summa
Lisää kaikki neliölliset poikkeamat yhteen. Tätä kutsutaan neliöiden summaksi.
16 + 361 + 324 + 100 + 4 + 81 = 886
Vaihe 5: Etsitään varianssi
Jaa neliöiden summa luvulla n – 1 (jos kyseessä on otos) tai N (jos kyseessä on populaatio) – tämä on varianssi.
Koska otoskoko on 6, käytämme n – 1, jossa n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Vaihe 6: Etsi varianssin neliöjuuri
Keskihajonnan löytämiseksi otetaan varianssin neliöjuuri.
√177,2 = 13,31
Oppiessamme, että SD = 13.31, voimme sanoa, että jokainen pistemäärä poikkeaa keskiarvosta keskimäärin 13,31 pistettä.
Miksi keskihajonta on käyttökelpoinen vaihtelun mittari?
Vaikka on olemassa yksinkertaisempiakin tapoja laskea vaihtelua, keskihajonnan kaava painottaa epätasaisesti jakautuneita otoksia enemmän kuin tasaisesti jakautuneita otoksia. Suurempi keskihajonta kertoo, että jakauma on paitsi hajanaisempi myös epätasaisemmin jakautunut.
Tämä tarkoittaa, että se antaa paremman käsityksen aineistosi vaihtelusta kuin yksinkertaisemmat mittarit, kuten absoluuttinen keskihajonta (MAD, Mean Absolute Deviation).
MAD on samankaltainen kuin keskihajonta, mutta helpompi laskea. Ensin ilmaiset jokaisen poikkeaman keskiarvosta absoluuttisina arvoina muuntamalla ne positiivisiksi luvuiksi (esimerkiksi -3 muuttuu 3:ksi). Sitten lasketaan näiden absoluuttisten poikkeamien keskiarvo.
Toisin kuin standardipoikkeaman kohdalla, MAD:n kohdalla ei tarvitse laskea lukujen neliöitä tai neliöjuuria. Tästä syystä se antaa kuitenkin epätarkemman mittarin vaihtelusta.
Otetaan kaksi otosta, joilla on sama keskitendenssi, mutta eri määrä vaihtelua. Näyte B on vaihtelevampi kuin näyte A.
| Arvot | Keskiarvo | Absoluuttinen keskihajonta | Keskiarvo | Keskihajonta | |
|---|---|---|---|---|---|
| Osake A | 66, 30, 40, 64 | 50 | 15 | 17.8 | |
| Osake B | 51, 21, 79, 49 | 50 | 15 | 23.7 |
Osakkeille, joiden keskimääräiset poikkeamat keskiarvosta ovat yhtä suuret, MAD ei pysty erottelemaan hajonnan tasoja. Keskihajonta on tarkempi: se on suurempi otokselle, jonka poikkeamat keskiarvosta vaihtelevat enemmän.
Keskihajonta kuvastaa epätasaista hajontaa tarkemmin neliöimällä erot keskiarvosta. Tämä vaihe painottaa äärimmäisiä poikkeamia enemmän kuin pieniä poikkeamia.
Tämä tekee kuitenkin myös keskihajonnasta herkän poikkeaville poikkeamille.
Tiheästi kysyttyjä kysymyksiä keskihajonnasta
Vaihtelua mitataan yleisimmin seuraavilla kuvailevilla tilastoilla:
- Vaihteluväli: suurimman ja pienimmän arvon välinen ero
- Interkvartiiliväli: jakauman keskimmäisen puoliskon vaihteluväli
- Keskihajonta: keskimääräinen etäisyys keskiarvosta
- Varianssi: keskiarvosta olevien neliöetäisyyksien keskiarvo
Keskihajonta on keskimääräinen vaihtelun määrä aineistossasi. Se kertoo, kuinka kaukana kukin arvo keskimäärin on keskiarvosta.
Normaalijakaumissa suuri keskihajonta tarkoittaa, että arvot ovat yleensä kaukana keskiarvosta, kun taas pieni keskihajonta osoittaa, että arvot ovat ryhmittyneet lähelle keskiarvoa.
Normaalijakaumassa data on symmetrisesti jakautunutta ilman vinoutta. Useimmat arvot ryhmittyvät keskialueen ympärille, ja arvot kapenevat, kun ne etääntyvät kauemmas keskipisteestä.
Keskisuuntauksen mittarit (keskiarvo, moodi ja mediaani) ovat täsmälleen samat normaalijakaumassa.
Empiirinen sääntö eli 68-95-99,7-sääntö kertoo, missä suurin osa arvoista sijaitsee normaalijakaumassa:
- Ympäri 68 % arvoista on yhden keskihajonnan sisällä keskiarvosta.
- Yli 95 % arvoista on kahden keskihajonnan sisällä keskiarvosta.
- Yli 99.7 % arvoista on 3 keskihajonnan sisällä keskiarvosta.
Empiirinen sääntö on nopea tapa saada yleiskuva tiedoistasi ja tarkastaa, onko poikkeamia tai ääriarvoja, jotka eivät noudata tätä kaavaa.
Varianssi on keskimääräinen neliöpoikkeama keskiarvosta, kun taas keskihajonta on tämän luvun neliöjuuri. Molemmat mittarit kuvastavat jakauman vaihtelua, mutta niiden yksiköt eroavat toisistaan:
- Keskihajonta ilmaistaan samoissa yksiköissä kuin alkuperäiset arvot (esim. minuutit tai metrit).
- Varianssi ilmaistaan paljon suuremmissa yksiköissä (esim. metrit neliöinä).
Vaikkakin varianssin yksikköjä on vaikeampi intuitiivisesti hahmottaa, varianssilla on tärkeä merkitys tilastollisissa testeissä.