MesopotamianEdit
Jaksolla 2700-2300 eaa. ilmestyi ensimmäisen kerran sumerilaisten abakus, peräkkäisistä sarakkeista koostuva taulukko, joka rajasi heidän sekagesimaalilukujärjestelmänsä peräkkäiset suuruusluokat.
Jotkut tutkijat viittaavat babylonialaisessa kiilakirjoituksessa esiintyvään merkkiin, joka on saattanut juontua abakuksen edustuksesta. Vanhan Babylonian tutkijat, kuten Carruccio, uskovat, että vanhat babylonialaiset ”saattoivat käyttää abakusta yhteen- ja vähennyslaskuoperaatioihin; tätä alkeellista laitetta oli kuitenkin vaikea käyttää monimutkaisempiin laskutoimituksiin”.
EgyptianEdit
Abakuksen käytön muinaisessa Egyptissä mainitsee kreikkalainen historioitsija Herodotos, joka kirjoittaa, että egyptiläiset manipuloivat kiviä oikealta vasemmalle, vastakkaiseen suuntaan kuin kreikkalaiset vasemmalta oikealle -menetelmällä. Arkeologit ovat löytäneet erikokoisia muinaisia kiekkoja, joiden uskotaan toimineen laskureina. Tästä välineestä ei kuitenkaan ole löydetty seinäkuvia.
PersialaisetEdit
Akhamenidien valtakunnan aikana, noin vuonna 600 eaa. persialaiset alkoivat ensimmäisen kerran käyttää abakusta. Parthian, Sassanian ja Iranin valtakuntien aikana oppineet keskittyivät vaihtamaan tietoa ja keksintöjä ympäröivien maiden – Intian, Kiinan ja Rooman keisarikunnan – kanssa, jolloin sen uskotaan vieneen sitä myös muihin maihin.
GreekEdit
Varhaisimmat arkeologiset todisteet kreikkalaisen abakuksen käytöstä ajoittuvat 5. vuosisadalle eaa. Myös Demosthenes (384 eaa. – 322 eaa.) puhui tarpeesta käyttää kiviä pään kannalta liian vaikeisiin laskutoimituksiin. Alexiksen näytelmässä 4. vuosisadalta eaa. mainitaan abakus ja kiviä laskutoimituksia varten, ja sekä Diogenes että Polybios mainitsevat miehiä, jotka välillä merkitsivät enemmän ja välillä vähemmän, kuten abakuksen kivet. Kreikkalainen abakus oli puinen tai marmorinen pöytä, johon oli valmiiksi asetettu pieniä puisia tai metallisia laskureita matemaattisia laskutoimituksia varten. Kreikkalainen abakus oli käytössä Akhamenidien Persiassa, etruskien sivilisaatiossa, muinaisessa Roomassa ja Ranskan vallankumoukseen asti läntisessä kristillisessä maailmassa.
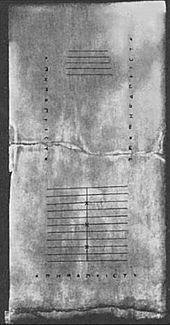
Kreikkalaiselta Salamisin saarelta vuonna 1846 jKr. löydetty taulu (Salamisin taulu) on peräisin vuodelta 300 eKr., mikä tekee siitä vanhimman tähän mennessä löydetyn laskutaulun. Se on 149 cm (59 tuumaa) pitkä, 75 cm (30 tuumaa) leveä ja 4,5 cm (2 tuumaa) paksu valkoisesta marmorista valmistettu laatta, jossa on viisi merkintäryhmää. Taulun keskellä on 5 samansuuntaista viivaa, jotka on jaettu tasan pystysuoralla viivalla ja joiden päällä on puoliympyrä alimman vaakasuoran viivan ja ainoan pystysuoran viivan leikkauspisteessä. Näiden viivojen alapuolella on leveä tila, jota jakaa vaakasuora halkeama. Tämän halkeaman alapuolella on toinen yhdentoista yhdensuuntaisen viivan ryhmä, joka on jälleen jaettu kahteen osaan viivalla, joka on kohtisuorassa näihin viivoihin nähden, mutta jonka leikkauspisteen yläreunassa on puoliympyrä; kolmas, kuudes ja yhdeksäs näistä viivoista on merkitty ristillä pystysuoran viivan leikkauspisteeseen. Samalta ajalta on myös vuonna 1851 kaivettu esiin Dariuksen maljakko. Se oli päällystetty kuvilla, joihin kuului muun muassa ”rahastonhoitaja”, joka pitelee toisessa kädessään vahataulua samalla, kun hän toisella kädellään manipuloi pöydällä olevia laskureita.
KiinanEdit

| Abakus | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditionaalinen kiinalainen | 算盤 | |||||||||||||||
| Yleistetty kiinalainen | 算盘 | |||||||||||||||
| Literaalinen. merkitys | ”laskutarjotin” | |||||||||||||||
| Transkriptiot | Standardi mandariini | Hanyu Pinyin | IPA | Yue: Kantonin kieli | Yale-romanisaatio | Jyutping | IPA | Southern Min | Hokkien POJ | Tâi-lô | ||||||
Varhaisin tunnettu kirjallinen dokumentaatio kiinalaisesta abakuksesta ajoittuu 2. vuosisadalle eKr.
Kiinalainen abakus, joka tunnetaan nimellä suanpan (算盤/算盘, lit. ”laskutarjotin”), on tyypillisesti 20 cm (8 tuumaa) korkea ja sitä on saatavana eri leveyksinä käyttäjästä riippuen. Siinä on yleensä yli seitsemän tankoa. Kussakin sauvassa on kaksi helmeä yläkannessa ja viisi helmeä kussakin alakannessa. Helmet ovat yleensä pyöristettyjä ja kovapuusta valmistettuja. Helmet lasketaan siirtämällä niitä ylös tai alas kohti palkkia; palkkia kohti siirrettyjä helmiä lasketaan, kun taas siitä poispäin siirrettyjä ei lasketa. Yksi ylhäällä olevista helmistä on 5, kun taas yksi alhaalla olevista helmistä on 1. Jokaisen sauvan alla on numero, joka osoittaa paikka-arvon.suanpan voi palauttaa alkuasentoonsa välittömästi nopealla liikkeellä vaaka-akselia pitkin, jolloin kaikki helmet pyörivät poispäin keskellä olevasta vaakasuorasta palkista.
Kiinalaisen abakuksen prototyyppi ilmestyi Han-dynastian aikana, ja sen helmet ovat soikeita. Song-dynastia ja sitä ennen käytettiin 1:4-tyyppistä eli neljän helmen abakusta, joka on samanlainen kuin nykyaikainen abakus, mukaan lukien helmien muoto, joka tunnetaan yleisesti japanilaistyylisenä abakuksena.
Ming-dynastian alkupuolella abakus alkoi ilmestyä 1:5-muotoisena abakuksena. Ylemmässä kannessa oli yksi helmi ja alemmassa viisi helmeä.
Ming-dynastian loppupuolella abakustyylit ilmestyivät 2:5-muotoisina. Ylemmässä kannessa oli kaksi helmeä ja alemmassa viisi helmeä.
Suanpanille kehitettiin erilaisia laskutekniikoita, jotka mahdollistivat tehokkaan laskemisen. Nykyisin on olemassa kouluja, joissa opetetaan sen käyttöä.
Zhang Zeduanin Song-dynastian aikana (960-1297) maalaamassa pitkässä Zhang Zeduanin pitkin jokea Qingming-festivaalin aikana -teoksessa suanpan näkyy selvästi apteekin (Feibao) tiskipöydällä olevan tilikirjan ja lääkärin reseptien vieressä.
Roomalaisen abakuksen ja kiinalaisen abakuksen samankaltaisuus viittaa siihen, että toinen on voinut inspiroida toista, sillä Rooman valtakunnan ja Kiinan välisestä kauppasuhteesta on todisteita. Mitään suoraa yhteyttä ei kuitenkaan voida osoittaa, ja abakusten samankaltaisuus voi olla sattumaa, sillä molemmat ovat viime kädessä peräisin laskemisesta viidellä sormella kättä kohti. Roomalaisessa mallissa (kuten useimmissa nykyaikaisissa korealaisissa ja japanilaisissa) on 4 plus 1 helmi per desimaali, kun taas tavallisessa suanpanissa on 5 plus 2. Tämä mahdollistaa muuten käytön heksadesimaalilukujärjestelmässä (tai missä tahansa emäksessä 18:aan asti), jota on saatettu käyttää perinteisissä kiinalaisissa painomittareissa. (Roomalaisen mallin helmet kulkevat urissa sen sijaan, että ne kulkisivat langoilla, kuten kiinalaisissa, korealaisissa ja japanilaisissa malleissa, mikä oletettavasti tekee aritmeettisista laskutoimituksista paljon hitaampia.
Toinen mahdollinen suanpanin lähde on kiinalaiset laskutangot, jotka toimivat desimaalijärjestelmällä, mutta joista puuttui nollan konsepti paikan osoittajana. Nolla otettiin luultavasti käyttöön kiinalaisilla Tang-dynastian aikana (618-907), jolloin matkat Intian valtamerellä ja Lähi-idässä olisivat mahdollistaneet suorat yhteydet Intiaan, jolloin kiinalaiset saivat nollan ja desimaalipisteen käsitteen intialaisilta kauppiailta ja matemaatikoilta.
RomanEdit

Tavanomainen laskutapa antiikin Roomassa, kuten myös Kreikassa, oli laskujen liikuttelu sileällä pöydällä. Alun perin käytettiin kiviä (calculi). Myöhemmin ja keskiajan Euroopassa valmistettiin jetoneja. Merkityt viivat osoittivat yksiköitä, vitosia, kymppejä jne. kuten roomalaisessa numerojärjestelmässä. Tämä ”laskurivalujärjestelmä” jatkui Rooman valtakunnan loppupuolella ja keskiajan Euroopassa, ja sitä käytettiin rajoitetusti vielä 1800-luvulla. Koska paavi Sylvester II otti abakuksen uudelleen käyttöön muutoksin, sitä alettiin käyttää Euroopassa laajalti jälleen 1100-luvulla. Tässä abakuksessa käytettiin langoilla olevia helmiä, toisin kuin perinteisissä roomalaisissa laskutauluissa, minkä ansiosta abakusta voitiin käyttää paljon nopeammin.
Kirjoittaessaan 1. vuosisadalla eaa. Horatius viittaa vaha-akkeliin, joka oli ohuella mustalla vahakerroksella päällystetty taulu, johon kirjoitettiin pylväitä ja lukuja kynällä.
Yksi esimerkki roomalaisesta abakkelista, joka on kuvassa rekonstruktiossa, on peräisin 1. vuosisadalta jKr. Siinä on kahdeksan pitkää uraa, joissa kussakin on enintään viisi helmeä, ja kahdeksan lyhyempää uraa, joissa kussakin on joko yksi tai ei yhtään helmeä. I:llä merkitty ura osoittaa yksiköitä, X kymmeniä ja niin edelleen miljooniin. Lyhyemmissä urissa olevat helmet merkitsevät viittä – viittä yksikköä, viittä kymppiä jne., lähinnä roomalaisiin numeroihin liittyvässä kaksinumeroisessa koodatussa desimaalijärjestelmässä. Oikeanpuoleisia lyhyitä uria on saatettu käyttää roomalaisten ”untsien” (eli murtolukujen) merkitsemiseen.
IndianEdit
Vasubandhun (316-396) Abhidharmakośabhāṣya, sanskritinkielinen teos buddhalaisesta filosofiasta, kertoo, että toisen vuosisadan jKr. filosofi Vasumitra sanoi, että ”kun asetetaan sydänlanka (sanskritiksi vartikā) numeron yksi (ekāṅka) päälle, se tarkoittaa, että se on yksi, kun taas kun asetetaan sydänlanka numeron sata päälle, se tarkoittaa, että sitä kutsutaan sadaksi, ja numeron tuhat päälle, se tarkoittaa, että se on tuhat”. On epäselvää, mikä tämä järjestely on tarkalleen ottaen voinut olla. Viidennen vuosisadan tienoilla intialaiset kirjanpitäjät keksivät jo uusia tapoja kirjata abakuksen sisältöä. Hinduteksteissä käytettiin termiä śūnya (nolla) osoittamaan abakuksen tyhjää saraketta.
japaniEdit

Japanissa abakusta käytetään nimitystä soroban (算盤, そろばん, sananmukaisesti ”laskutarjotin”), joka tuotiin Kiinasta 1300-luvulla. Se oli luultavasti työväenluokan käytössä vähintään sata vuotta ennen kuin hallitseva luokka alkoi käyttää sitä, sillä luokkarakenne ei sallinut alemman luokan käyttämien välineiden omaksumista tai käyttöä hallitsevassa luokassa. 1/4-abakus, jossa harvoin käytetty toinen ja viides helmi poistetaan, tuli suosituksi 1940-luvulla.
Tämän päivän japanilainen abakus on 1:4-tyyppinen, neljän helmen abakus, joka tuotiin Kiinasta Muromachi-kaudella. Se omaksuu muodon, jossa yläkannella on yksi helmi ja alakannella neljä helmeä. Yläkannen ylin helmi oli yhtä suuri kuin viisi ja alin yhtä suuri kuin yksi, kuten kiinalaisessa tai korealaisessa abakuksessa, ja desimaaliluku voidaan ilmaista, joten abakus on suunniteltu yhdeksi neljäksi abakukseksi. Helmet ovat aina timantin muotoisia. Osamääräistä jakoa käytetään yleensä jakomenetelmän sijasta; samaan aikaan, jotta kertolasku- ja jakoluvut saadaan johdonmukaisesti käyttämään jakokertolaskua. Myöhemmin Japanissa oli 3:5 abakus nimeltään 天三算盤, joka on nyt Yamagatan kaupungin Shansi-kylän Ize Rongjin kokoelma. Siellä oli myös 2:5-tyyppisiä abakuksia.
Nelihelmisen abakuksen levittäytymisen myötä japanilaisia abakuksia käytetään myös yleisesti ympäri maailmaa. Eri paikoissa on myös paranneltuja japanilaisia abakuksia. Yksi Kiinassa valmistettu japanilainen abakus on alumiinirunkoinen muovihelmiabakus. Tiedosto on neljän helmen vieressä, ja ”clearing” -painike, paina clearing-painiketta, laita välittömästi ylempi helmi ylempään asentoon, alempi helmi valitaan alempaan asentoon, välittömästi clearing, helppokäyttöinen.
Abaakki valmistetaan edelleen Japanissa nykyäänkin, vaikka tasku-elektronisten laskinten yleistyminen, käytännöllisyys ja kohtuuhintaisuus. Sorobanin käyttöä opetetaan edelleen japanilaisissa peruskouluissa osana matematiikkaa, ensisijaisesti nopeamman mielenlaskun apuvälineenä. Käyttämällä visuaalisia mielikuvia sorobanista voidaan päästä vastaukseen samassa ajassa tai jopa nopeammin kuin fyysisellä välineellä on mahdollista.
KoreanEdit
Kiinalainen abakus siirtyi Kiinasta Koreaan noin 1400 jKr. Korealaiset kutsuvat sitä jupaniksi (주판), supaniksi (수판) tai jusaniksi (주산).Neljän helmen abakus( 1:4 ) tuotiin Koreaan Goryeo-dynastian aikana Kiinasta Song-dynastian aikana, myöhemmin viiden helmen abakus (5:1) tuotiin Koreaan Kiinasta Ming-dynastian aikana.
AlkuperäisamerikkalainenEdit


Jotkut lähteet mainitsevat nepohualtzintzin-nimisen abakuksen käytön muinaisessa atsteekkien kulttuurissa. Tämä mesoamerikkalainen abakus käytti 5-numeroista perusta-20-järjestelmää. sana Nepōhualtzintzin tulee Nahuatl-kielestä, ja se muodostuu juurista; Ne – henkilökohtainen -; pōhual tai pōhualli – tili -; ja tzintzin – pienet samankaltaiset elementit. Sen täydellisenä merkityksenä pidettiin: jonkun tekemä laskenta pienillä samankaltaisilla elementeillä. Sen käyttöä opetettiin Calmecacissa temalpouhquehille , jotka olivat oppilaita, jotka olivat omistautuneet ottamaan tiliä taivaista, lapsesta asti.
Nepōhualtzintzin oli jaettu kahteen pääosaan, jotka erotti toisistaan palkki tai välijohto. Vasemmassa osassa oli neljä helmeä, joiden ensimmäisellä rivillä oli yksikköarvot (1, 2, 3 ja 4), ja oikeassa osassa oli kolme helmeä, joiden arvot olivat vastaavasti 5, 10 ja 15. Ylempien rivien vastaavien helmien arvon tietämiseksi riittää, että kerrotaan 20:llä (kullakin rivillä) ensimmäisen rivin vastaavan tilin arvo.
Kokonaisuudessaan rivejä oli 13, joissa kussakin oli 7 helmeä, mikä muodosti 91 helmeä kussakin Nepōhualtzintzinissä. Tämä oli perusluku, jonka ymmärtäminen, 7 kertaa 13, oli luonnonilmiöiden, alamaailman ja taivaan syklien välille ajateltu läheinen suhde. Yksi Nepōhualtzintzin (91) edusti niiden päivien lukumäärää, jotka yksi vuodenaika kestää, kaksi Nepōhualtzintzinia (182) on maissin kiertokulun päivien lukumäärä kylvöstä sadonkorjuuseen, kolme Nepōhualtzintzinia (273) on vauvan tiineyden päivien lukumäärä, ja neljä Nepōhualtzintzinia (364) täydensi kiertokulun ja vastasi suunnilleen vuotta (11/4 päivää vajaa). Kun Nepōhualtzintzin käännetään nykyaikaiseen tietokonearitmetiikkaan, Nepōhualtzintzin oli arvoasteikko 10:stä 18:aan kelluvassa pisteessä, joka laski tähtimääriä sekä äärettömiä määriä absoluuttisella tarkkuudella, mikä tarkoitti, että pyöristyksiä ei sallittu.
Nepōhualtzintzinin uudelleen löytäminen oli meksikolaisen insinöörin David Esparza Hidalgon ansiota, joka vaelluksillaan eri puolilla Meksikoa löysi erilaisia kaiverruksia ja maalauksia tästä instrumentista ja rekonstruoi useita niistä, jotka oli tehty kullasta, jadesta, simpukkakuorien kuorista jne. On myös löydetty hyvin vanhoja Nepōhualtzintzinkejä, jotka on liitetty Olmec-kulttuuriin, ja jopa joitakin Maya-peräisiä rannekoruja sekä monenlaisia muotoja ja materiaaleja muista kulttuureista.
George I. Sanchez, ”Arithmetic in Maya”, Austin-Texas, 1961, löysi Jukatanin niemimaalta toisen 5:n ja 4:n perustan abakuksen, joka laski myös kalenteritietoja. Kyseessä oli sormiabakus, jossa yhdellä kädellä käytettiin 0, 1, 2, 3 ja 4 ja toisella kädellä 0, 1, 2 ja 3. Huomaa nollan käyttö kahden syklin alussa ja lopussa. Sanchez työskenteli yhdessä Sylvanus Morleyn kanssa, joka oli tunnettu mayatutkija.
Inkojen quipu oli värillisistä solmituista naruista koostuva järjestelmä, jota käytettiin numeeristen tietojen kirjaamiseen, kuten kehittyneitä laskutikkuja – mutta jota ei käytetty laskutoimituksiin. Laskutoimitukset suoritettiin yupanalla (quechua tarkoittaa ”laskentatyökalua”; ks. kuva), joka oli käytössä vielä Perun valloituksen jälkeen. Yupanan toimintaperiaatetta ei tunneta, mutta italialainen matemaatikko Nicolino De Pasquale esitti vuonna 2001 selityksen näiden välineiden matemaattisesta perustasta. Vertailemalla useiden yupanoiden muotoa tutkijat havaitsivat, että laskutoimitukset perustuivat Fibonacci-sekvenssiin 1, 1, 2, 3, 5 ja potensseihin 10, 20 ja 40 instrumentin eri kenttien paikka-arvoina. Fibonacci-sekvenssin käyttäminen piti jyvien määrän yhden kentän sisällä mahdollisimman pienenä.
RussianEdit

Venäläinen abakus, skoty (venäjänkielestä счёты, monikko venäjänkielestä: счёт, laskeminen), on yleensä yksi vino kansi, jossa on kymmenen helmeä jokaisessa langassa (paitsi yhdessä langassa, joka on yleensä sijoitettu lähelle käyttäjää ja jossa on neljä helmeä neljännesruplan murtolukuja varten). Vanhemmissa malleissa on vielä yksi neljän helmen lanka neljänneskopekkeja varten, joita lyötiin vuoteen 1916 asti. Venäläistä abakusta käytetään usein pystysuorassa, jolloin jokainen lanka kulkee vasemmalta oikealle kuin kirjan rivit. Johtimet on yleensä taivutettu niin, että ne pullistuvat keskeltä ylöspäin, jotta helmet pysyvät kiinni jommallakummalla sivulla. Se tyhjennetään, kun kaikki helmet siirretään oikealle. Manipulaation aikana helmiä siirretään vasemmalle. Katsomisen helpottamiseksi kunkin langan kaksi keskimmäistä helmeä (5. ja 6. helmi) ovat yleensä erivärisiä kuin muut kahdeksan muuta helmeä. Samoin tuhannen langan vasemmanpuoleinen helmi (ja mahdollinen miljoonan lanka) voi olla erivärinen.
Yksinkertaisena, halpana ja luotettavana laitteena venäläinen abakus oli käytössä kaikissa kaupoissa ja marketeissa koko entisen Neuvostoliiton alueella, ja sen käyttöä opetettiin useimmissa kouluissa 1990-luvulle asti. Edes vuonna 1874 keksitty mekaaninen laskin, Odhnerin aritmometri, ei ollut korvannut niitä Venäjällä; Jakov Perelmanin mukaan jo hänen aikanaan joidenkin liikemiesten, jotka yrittivät tuoda tällaisia laitteita Venäjän keisarikuntaan, tiedettiin luovuttaneen ja lähteneen epätoivoissaan sen jälkeen, kun heille oli näytetty ammattitaitoisen abakusikäyttäjän työ. Myöskään Felix-aritometrien massatuotanto vuodesta 1924 lähtien ei vähentänyt merkittävästi niiden käyttöä Neuvostoliitossa. Venäläinen abakus alkoi menettää suosiotaan vasta sen jälkeen, kun Neuvostoliitossa oli aloitettu mikrolaskimien massatuotanto vuonna 1974. Nykyään sitä pidetään arkaaismana, ja se on korvattu kädessä pidettävällä laskimella.
Venäläisen abakuksen toi Ranskaan noin vuonna 1820 matemaatikko Jean-Victor Poncelet, joka palveli Napoleonin armeijassa ja oli ollut sotavankina Venäjällä. Abakus oli jäänyt pois käytöstä Länsi-Euroopassa 1500-luvulla desimaalilaskennan ja algorismimenetelmien yleistyessä. Poncelet’n ranskalaisille aikalaisille se oli jotain uutta. Poncelet ei käyttänyt sitä mihinkään soveltavaan tarkoitukseen vaan opetuksen ja esittelyn apuvälineenä. Myös turkkilaiset ja armenialaiset käyttivät venäläisen skotyn kaltaisia abakuksia. Turkkilaiset kutsuivat sitä coulbaksi ja armenialaiset chorebiksi.