A Concise Introduction to Logic

9.1 Historiallinen esimerkki

Filosofi David Hume (1711-1776) muistetaan loistavana skeptisenä empiristinä. Henkilö on skeptikko jonkin aiheen suhteen, jos hänellä on sekä hyvin tiukat vaatimukset sille, mikä on tietoa kyseisestä aiheesta, että hän uskoo, ettemme voi täyttää näitä tiukkoja vaatimuksia. Empirismi on näkemys, jonka mukaan saamme tietoa ensisijaisesti kokemuksen kautta, erityisesti aistiemme kautta. Kirjassaan An Inquiry Concerning Human Understanding Hume esittää tietämystä koskevat periaatteensa ja neuvoo meitä sitten siivoamaan kirjastomme:

Kun juoksemme kirjastojen yli, vakuuttuneina näistä periaatteista, mitä tuhoa meidän on tehtävä? Jos otamme käteemme esimerkiksi minkä tahansa jumaluusopin tai koulumetafysiikan teoksen, kysykäämme: Sisältääkö se mitään abstraktia päättelyä, joka koskee määrää tai lukumäärää? Ei. Sisältääkö se mitään kokeellista päättelyä, joka koskee tosiasioita ja olemassaoloa? Ei. Toimittakaa se sitten liekkeihin, sillä se ei voi sisältää muuta kuin sofistiikkaa ja harhaa.”

Hume oli sitä mieltä, että ainoat tiedon lähteet olivat looginen tai matemaattinen päättely (jota hän kutsuu edellä ”abstraktiksi päättelyksi, joka koskee paljoutta tai lukumäärää”) tai aistikokemus (”kokeellinen päättely, joka koskee tosiasioita ja olemassaoloa”). Hume päätyy väittämään, että kaikki väitteet, jotka eivät perustu jompaankumpaan menetelmään, ovat arvottomia.

Voidaan rekonstruoida Humen argumentti seuraavalla tavalla. Oletetaan, että t on jokin aihe, josta väitämme, että meillä on tietoa. Oletetaan, että emme ole saaneet tätä tietoa kokemuksesta tai logiikasta. Suomeksi kirjoitettuna voimme rekonstruoida hänen argumenttinsa seuraavalla tavalla:

Meillä on tietoa t:stä, jos ja vain jos väitteemme t:stä on opittu kokeellisesta päättelystä tai logiikasta tai matematiikasta.

Väitteitämme t:stä ei opita kokeellisesta päättelystä.

Väitteitämme t:stä ei opita logiikasta tai matematiikasta.

Meillä ei ole tietoa t:stä.

Mitä tuo lause ”jos ja vain jos” tarkoittaa? Filosofit ajattelevat, että sitä ja useita synonyymejä lauseita käytetään usein päättelyssä. Kun jätämme ”jos ja vain” toistaiseksi selittämättä, voimme käyttää seuraavaa käännösavainta kirjoittaaksemme argumentin sekoituksella meidän propositionaalista logiikkaamme ja englantia.

P: Meillä on tietoa t:stä.

Q: Väitteemme t:stä on opittu kokeellisesta päättelystä.

R: Väitteemme t:stä on opittu logiikasta tai matematiikasta.

Ja näin meillä on:

P jos ja vain jos (QvR)

¬Q

¬R

¬P

Tehtävämme on lisätä loogiseen kieleemme ekvivalentti lauseelle ”jos ja vain jos”. Sitten voimme arvioida tätä Humen argumentin uudelleenmuotoilua.

9.2 Bikonditionaali

Ennen kuin esittelemme symbolin, joka on synonyymi sanalle ”jos ja vain jos”, ja sen jälkeen hahmotamme sen syntaksin ja semantiikan, meidän on aloitettava eräästä huomautuksesta. Lause ”P jos ja vain jos Q” näyttää olevan lyhennetty tapa sanoa ”P jos Q ja P vain jos Q”. Kun huomaamme tämän, meidän ei tarvitse yrittää selvittää ”if and only if” -sanan merkitystä englannin kielen asiantuntevan ymmärryksemme avulla. Sen sijaan voimme selvittää ”if and only if” -sanan merkityksen käyttämällä ”if”, ”and” ja ”only if” -sanojen jo valmiiksi tarkkoja määritelmiä. Erityisesti ”P jos Q ja P vain jos Q” käännetään ”((Q→P)^(P→Q))”. (Jos tämä on sinulle epäselvää, palaa takaisin ja lue kohta 2.2.) Tehdään nyt totuustaulukko tälle kaavalle.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T	T
T	F	T	T	F	F
F	T	F	T	F	F
F	F	T	T	T	T

Olemme ratkaisseet semantiikan ”jos ja vain jos”. Voimme nyt ottaa käyttöön uuden symbolin tälle lausekkeelle. Perinteisesti käytetään kaksoisnuolta, ”↔”. Voimme nyt ilmaista ”↔:n” syntaksin ja semantiikan:

Jos Φ ja Ψ ovat lauseita, niin

(Φ↔Ψ)

on lause. Tällaista lausetta kutsutaan tyypillisesti ”bikonditionaaliksi”.

Semantiikan antaa seuraava totuustaulukko.

.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	T	F
F	F	T

Bikonditionaalia koskevan selityksemme yksi ilahduttava tulos on, että sen avulla pystymme selittämään ytimekkäästi loogisen ekvivalenssin syntaktisen käsitteen. Sanomme, että kaksi lausetta Φ ja Ψ ovat ”ekvivalentteja” tai ”loogisesti ekvivalentteja”, jos (Φ↔Ψ) on lause.

9.3 Vaihtoehtoiset lausekkeet

Englannissa näyttää olevan useita lausekkeita, joilla on yleensä sama merkitys kuin bikonditionaalilla. Jokainen seuraavista lauseista käännettäisiin (P↔Q).

P jos ja vain jos Q.

P vain jos Q.

P on välttämätön ja riittävä Q:lle.

P on ekvivalentti Q:n kanssa.

9.4 Päätteleminen bikonditionaalilla

Miten voimme päättelemällä päätellä bikonditionaalin avulla? Aluksi näyttäisi siltä, että se tarjoaa vain vähän ohjeita. Jos tiedän, että (P↔Q), tiedän, että P:llä ja Q:lla on sama totuusarvo, mutta pelkästään tuon lauseen perusteella en tiedä, ovatko molemmat totta vai molemmat epätotta. Voimme kuitenkin hyödyntää bikonditionaalin semantiikkaa havaitaksemme, että jos tiedämme myös toisen bikonditionaalin muodostavan lauseen totuusarvon, voimme johtaa toisen lauseen totuusarvon. Tämä viittaa suoraviivaisiin sääntöihin. Näitä sääntöjä on itse asiassa neljä, mutta ryhmittelemme ne yhteen nimellä ”ekvivalenssi”:

ja

ja

ja

Mitä jos sen sijaan yritämme osoittaa bikonditionaalin? Tässä voimme palata siihen oivallukseen, että bikonditionaali (Φ↔Ψ) vastaa ((Φ→Ψ)^(Ψ→Φ)). Jos voisimme todistaa sekä (Φ→Ψ) että (Ψ→Φ), tietäisimme, että (Φ↔Ψ) täytyy olla tosi.

Voidaan kutsua tätä sääntöä ”bikonditionaaliksi”. Se on seuraavassa muodossa:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Tämä tarkoittaa, että usein, kun pyrimme todistamaan bikonditionaalin, ryhdymme suorittamaan kahta konditionaalista derivaatiota kahden konditionaalin johtamiseksi ja käytämme sitten bikonditionaalisääntöä. Toisin sanoen monet bikonditionaalien todistukset ovat seuraavassa muodossa:

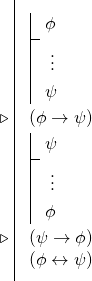
9.5 Palataan Humeen

Voidaan nyt katsoa, pystymmekö todistamaan Humen argumentin. Koska meillä on nyt uusi bikonditionaalinen symboli, voimme aloittaa suoran todistuksen kolmella premissiollamme.

Olemme jo havainneet, että mielestämme (QvR) on väärä, koska ¬Q ja ¬R. Todistetaan siis ¬(QvR). Tätä lausetta ei voida todistaa suoraan, kun otetaan huomioon meillä olevat premissiot; eikä sitä voida todistaa ehdollisella todistuksella, koska se ei ole ehdollinen. Kokeillaan siis epäsuoraa todistusta. Uskomme, että ¬(QvR) on tosi, joten oletamme tämän kieltämisen ja osoitamme ristiriidan.

Humen argumentti, ainakin sellaisena kuin rekonstruoimme sen, on pätevä.

Onko Humen argumentti pätevä? Se, onko se järkevä, riippuu edellä olevasta ensimmäisestä premissistä (koska toinen ja kolmas premissi ovat abstraktioita jostakin aiheesta t). Tarkemmin sanottuna se riippuu väitteestä, että meillä on tietoa jostakin asiasta vain siinä tapauksessa, että voimme osoittaa sen kokeella tai logiikalla. Hume väittää, että meidän tulisi epäluuloisesti luottaa – tai jopa polttaa – teksteihin, jotka sisältävät väitteitä, jotka eivät perustu kokeisiin ja havaintoihin tai logiikkaan ja matematiikkaan. Mutta ajatellaanpa tätä väitettä: meillä on tietoa jostakin aiheesta t, jos ja vain jos väitteemme t:stä on opittu kokeesta tai väitteemme t:stä on opittu logiikasta tai matematiikasta.

Oliko Hume havainnut tämän väitteen kokeiden avulla? Vai löysikö hän sen logiikan kautta? Minkä kohtalon Humen kirja kärsisi, jos noudattaisimme hänen neuvoaan?

9.6 Joitakin esimerkkejä

Voi olla hyödyllistä todistaa joitain teoreemoja, joissa käytetään bikonditionaalia, jotta voidaan havainnollistaa, miten voimme järkeillä bikonditionaalin avulla.

Tässä on hyödyllinen periaate. Jos kahdella lauseella on sama totuusarvo kuin kolmannella lauseella, niin niillä on sama totuusarvo keskenään. Toteamme tämän muodossa (((P↔Q)^(R↔Q))→(P↔R)). Jotta voimme havainnollistaa päättelyä bikonditionaalin avulla, todistetaan tämä lause.

Tämä lause on konditionaali, joten se vaatii konditionaalin johtamisen. Konditionaalin seuraus on bikonditionaalinen, joten odotamme tarvitsevamme kaksi konditionaalijohdannaista, yhden todistamaan (P→R) ja toisen todistamaan (R→P). Todistus näyttää seuraavalta. Tutki sitä tarkasti.

Olemme aiemmin maininneet periaatteet, jotka yhdistämme matemaatikko Augustus De Morganiin (1806-1871) ja joita nykyään kutsutaan ”De Morganin laeiksi” tai ”De Morganin ekvivalensseiksi”. Nämä ovat sen toteaminen, että ¬(PvQ) ja (¬P^¬Q) ovat ekvivalentteja ja että ¬(P^Q) ja (¬Pv¬Q) ovat ekvivalentteja. Voimme nyt ilmaista nämä bikonditionaalilla. Seuraavat ovat logiikkamme teoreemoja:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Todistamme näistä lauseista toisen. Tämä on ehkä vaikein näkemämme todistus; se vaatii sisäkkäisiä epäsuoria todistuksia ja melkoista nokkeluutta sen löytämisessä, mikä on relevantti ristiriita.

9.7 Teoreemojen käyttäminen

Jokainen logiikkamme lause on semanttisesti katsottuna yksi kolmesta lajista. Se on joko tautologia, ristiriitainen lause tai ehdollinen lause. Olemme jo määritelleet ”tautologian” (lause, jonka täytyy olla tosi) ja ”ristiriitaisen lauseen” (lause, jonka täytyy olla väärä). Ehdollinen lause on lause, joka ei ole tautologia eikä ristiriitainen lause. Kontingenttilause on siis lause, joka voi olla tosi tai väärä.

Tässä on esimerkki kummastakin lausetyypistä:

(Pv¬P)

(P↔¬P)

P

Ensimmäinen on tautologia, toinen on ristiriitainen lause ja kolmas kontingenttilause. Voimme nähdä tämän totuustaulukon avulla.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Huomaa, että tautologian negaatio on ristiriita, ristiriidan negaatio on tautologia, ja ehdollisen lauseen negaatio on ehdollinen lause.

¬(Pv¬P)

¬(P↔¬P)

¬P

P	¬P	(Pv¬P)	¬(Pv¬P)	(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	F	T	T
F	T	T	F	F	T

Hetken pohdiskelu paljastaa, että olisi aikamoinen katastrofi, jos propositiologiikan lauseemme olisi joko ristiriitainen lause tai kontingenttinen lause. Logiikkamme on suunniteltu tuottamaan vain päteviä väitteitä. Havaitsimme, että argumenteilla, joilla ei ole premissejä, pitäisi olla johtopäätöksiä, joiden on oltava tosia (tämä taas seuraa siitä, että lause, joka voidaan todistaa ilman premissejä, voidaan todistaa millä tahansa premisseillä, joten sen on parempi olla tosi riippumatta siitä, mitä premissejä käytämme). Jos lause olisi ristiriitainen, tietäisimme, että voisimme todistaa vääryyden. Jos lause olisi ehdollinen, voisimme joskus todistaa vääryyden (toisin sanoen voisimme todistaa lauseen, joka on tietyin ehdoin väärä). Ja kun otetaan huomioon, että olemme ottaneet epäsuoran derivoinnin todistusmenetelmäksi, siitä seuraa, että kun meillä on ristiriita tai ristiriitainen lause argumentissa, voimme todistaa mitä tahansa.

Teoriat voivat olla meille hyvin hyödyllisiä argumenteissa. Oletetaan, että tiedämme, ettei Smith eikä Jones mene Lontooseen, ja haluamme siis todistaa, ettei Jones mene Lontooseen. Jos antaisimme itsellemme luvan käyttää jotakin De Morganin teoreemaa, saisimme väitteen nopeasti ratkaistua. Oletetaan seuraava avain.

P: Smith menee Lontooseen.

Q: Jones menee Lontooseen.

Ja meillä on seuraava argumentti:

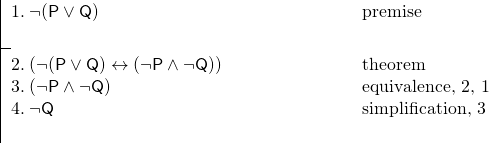
Tämä todistus on tehty hyvin helpoksi, kun käytimme rivillä 2 olevaa teoreemaa.

Tässä on kaksi huomautettavaa asiaa. Ensinnäkin meidän pitäisi sallia itsemme tehdä näin, koska jos tiedämme, että lause on teoreema, tiedämme, että voimme todistaa kyseisen teoreeman alitodistuksessa. Toisin sanoen voisimme korvata yllä olevan rivin 2 pitkällä osatodistuksella, joka todistaa (¬(P v Q)↔(¬P ^ ¬Q)), jota voisimme sitten käyttää. Mutta jos olemme varmoja siitä, että (¬(P v Q)↔(¬P ^ ¬Q)) on lause, meidän ei pitäisi joutua tekemään tätä todistusta uudestaan ja uudestaan joka kerta, kun haluamme käyttää kyseistä lausetta.

Toinen asia, joka meidän pitäisi tunnistaa, on hienovaraisempi. On olemassa äärettömän monta lausetta, jotka ovat lauseemme muotoisia, ja meidän pitäisi pystyä käyttämään myös niitä. Esimerkiksi seuraavilla lauseilla olisi kullakin samanlainen todistus kuin lauseemme todistus (¬(P v Q)↔(¬P ^ ¬Q)), paitsi että kirjaimet olisivat erilaiset:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Tämä on toivottavasti itsestään selvää. Otetaan todiste (¬(P v Q)↔(¬P ^ ¬Q)) ja korvataan tuossa todisteessa jokainen P:n esiintymä R:llä ja jokainen Q:n esiintymä S:llä, niin saadaan todiste (¬(R v S)↔(¬R ^ ¬S)).

Mutta tässä on jotakin, mikä ei ehkä ole yhtä ilmeistä. Jokaisen seuraavista voidaan ajatella olevan samanlainen kuin lause (¬(P v Q)↔(¬P ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S))↔(¬(P^Q) ^ ¬(R^S))↔(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))↔(¬(T v (Q v V))↔(¬(T ^ ¬(Q v V))↔(¬(T ^ ^ ¬(Q v V))↔(T ^ ^ ^ ¬(T ^ Q v V))↔(T ^ ^ ^ ^ ^ ^ ^ ^ Q v V))↔(T T ^ ^ ^ ^ ^ ^ ^ ^^ ^ ¿(P v V))).” (

Voisimme vangita tämän oivalluksen kahdella tavalla. Voisimme esittää metakielemme teoreemoja ja sallia, että niillä on esiintymiä. Siten voisimme ottaa (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) metakielen lauseeksi, jossa voisimme korvata jokaisen Φ:n lauseella ja jokaisen Ψ:n lauseella ja saada tietyn instanssin lauseesta. Vaihtoehtoisesti voidaan sallia, että teoreemasta voidaan tuottaa muita teoreemoja korvaamalla. Yksinkertaisuuden vuoksi valitsemme tämän toisen strategian.

Sääntömme on seuraava. Kun olemme todistaneet teoreeman, voimme milloin tahansa siteerata sitä todistuksessa. Perustelumme on, että väite on teoreema. Sallimme lauseen minkä tahansa atomilauseen korvaamisen millä tahansa muulla lauseella, jos ja vain jos korvaamme lauseen jokaisen kyseisen atomilauseen alkuesimerkin samalla lauseella.

Ennen kuin tarkastelemme esimerkkiä, on hyödyllistä luetella joitakin hyödyllisiä teoreemoja. Kielessämme on äärettömän monta teoreemaa, mutta nämä kymmenen ovat usein hyvin hyödyllisiä. Muutaman olemme todistaneet. Muut voidaan todistaa harjoitustyönä.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Jotkut esimerkit selventävät teoreemojen käyttämisen etuja. Tarkastellaan erilaista argumenttia, joka rakentuu edellä esitetylle. Tiedämme, että ei ole totta, että jos Smith menee Lontooseen, hän menee Berliiniin, eikä ole totta, että jos Jones menee Lontooseen, hän menee Berliiniin. Haluamme todistaa, että ei ole totta, että Jones menee Berliiniin. Lisäämme avaimeemme seuraavaa:

R: Smith menee Berliiniin.

S: Jones menee Berliiniin.

Ja saamme seuraavan väitteen:

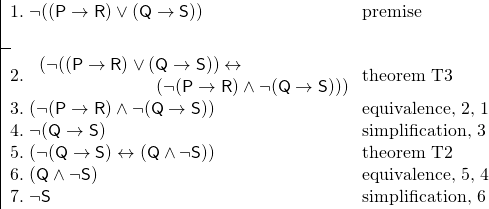
Toreemien käyttäminen teki tästä todisteesta paljon lyhyemmän kuin se muuten voisi olla. Lisäksi lauseet helpottavat usein todistuksen seuraamista, koska tunnistamme lauseet tautologioiksi – lauseiksi, joiden täytyy olla totta.

9.8 Ongelmat

1. Varmennetaan, että kukin seuraavista väitteistä on pätevä.

1. Väitteet: P, ¬Q. Johtopäätökset: ¬(P↔Q).
2. Premissiot: (¬PvQ), (Pv¬Q). Johtopäätös: (P↔Q).
3. Premises: (P↔Q), (R↔S) . Johtopäätös: ((P^R)↔(Q^S)).

1. Varmista jokainen seuraavista lauseista.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. T9
9. ((P^Q)↔¬(¬Pv¬Q))
10. ((P→Q)↔¬(P^¬Q))

1. Kirjoita tavallisella puhekielellä oma pätevä argumenttisi, jossa on vähintään kaksi premissiä, joista vähintään toinen on bikonditionaali. Argumenttisi pitäisi olla pelkkä kappale (ei järjestetty lauseiden luettelo tai mitään muuta muodollisen logiikan näköistä). Käännä se propositionaaliseen logiikkaan ja todista, että se on pätevä.
2. Kirjoita normaalilla puhekielisellä englannilla oma pätevä argumenttisi, jossa on vähintään kaksi premissiä ja jossa on johtopäätös, joka on bikonditionaali. Argumenttisi tulisi olla pelkkä kappale (ei järjestetty lauseiden luettelo tai mikään muu muodolliselta logiikalta näyttävä). Käännä se propositionaaliseen logiikkaan ja todista, että se on pätevä.