Una introducción concisa a la lógica

9.1 Un ejemplo histórico

El filósofo David Hume (1711-1776) es recordado por ser un brillante empirista escéptico. Una persona es escéptica sobre un tema si esa persona tiene normas muy estrictas sobre lo que constituye el conocimiento sobre ese tema y también cree que no podemos cumplir esas normas estrictas. El empirismo es el punto de vista de que obtenemos el conocimiento principalmente a través de la experiencia, en particular las experiencias de nuestros sentidos. En su libro, An Inquiry Concerning Human Understanding, Hume expone sus principios para el conocimiento, y luego nos aconseja limpiar nuestras bibliotecas:

Cuando recorremos las bibliotecas, persuadidos de estos principios, ¿qué estragos debemos hacer? Si tomamos en nuestra mano cualquier volumen de divinidad o de metafísica escolar, por ejemplo, preguntemos: ¿Contiene algún razonamiento abstracto relativo a la cantidad o al número? No. ¿Contiene algún razonamiento experimental relativo a la materia de hecho y a la existencia? No. Entonces envíalo a las llamas, porque no puede contener más que sofismas e ilusiones.

Hume consideraba que las únicas fuentes de conocimiento eran los razonamientos lógicos o matemáticos (a los que llama arriba «razonamientos abstractos sobre la cantidad o el número») o la experiencia de los sentidos («razonamientos experimentales sobre la materia de los hechos y la existencia»). Hume se ve llevado a argumentar que cualquier afirmación que no se base en uno u otro método carece de valor.

Podemos reconstruir el argumento de Hume de la siguiente manera. Supongamos que t es algún tema sobre el que afirmamos tener conocimiento. Supongamos que no obtuvimos este conocimiento de la experiencia o de la lógica. Escrito en inglés, podemos reconstruir su argumento de la siguiente manera:

Tenemos conocimiento sobre t si y sólo si nuestras afirmaciones sobre t se aprenden del razonamiento experimental o de la lógica o las matemáticas.

Nuestras afirmaciones sobre t no se aprenden del razonamiento experimental.

Nuestras afirmaciones sobre t no se aprenden de la lógica o de las matemáticas.

No tenemos conocimiento sobre t.

¿Qué significa esa frase «si y sólo si»? Los filósofos piensan que ella, y varias frases sinónimas, se utilizan a menudo en los razonamientos. Dejando «si y sólo si» sin explicar por ahora, podemos usar la siguiente clave de traducción para escribir el argumento en una mezcla de nuestra lógica proposicional y el inglés.

P: Tenemos conocimiento sobre t.

Q: Nuestras afirmaciones sobre t se aprenden del razonamiento experimental.

R: Nuestras afirmaciones sobre t se aprenden de la lógica o las matemáticas.

Y así tenemos:

P si y sólo si (QvR)

¬Q

¬R

¬P

Nuestra tarea es añadir a nuestro lenguaje lógico un equivalente a «si y sólo si». Entonces podremos evaluar esta reformulación del argumento de Hume.

9.2 El bicondicional

Antes de introducir un símbolo sinónimo de «si y sólo si», y de exponer luego su sintaxis y semántica, debemos comenzar con una observación. Una frase como «P si y sólo si Q» parece ser una forma abreviada de decir «P si Q y P sólo si Q». Una vez que nos damos cuenta de esto, no tenemos que intentar discernir el significado de «if and only if» utilizando nuestra comprensión experta del inglés. En su lugar, podemos discernir el significado de «if and only if» utilizando nuestras ya rigurosas definiciones de «if», «and» y «only if». En concreto, «P si Q y P sólo si Q» se traducirá «((Q→P)^(P→Q))». (Si esto no te queda claro, vuelve a repasar la sección 2.2.) Ahora, hagamos una tabla de verdad para esta fórmula.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T	T
T	F	T	F	F
F	T	F	T	F
F	F	T	T	T

Hemos resuelto la semántica de «si y sólo si». Ahora podemos introducir un nuevo símbolo para esta expresión. Es tradicional utilizar la flecha doble, «↔». Ahora podemos expresar la sintaxis y la semántica de «↔».

Si Φ y Ψ son oraciones, entonces

(Φ↔Ψ)

es una oración. Este tipo de sentencia se llama típicamente «bicondicional».

La semántica viene dada por la siguiente tabla de verdad.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

Un resultado agradable de nuestra cuenta del bicondicional es que nos permite explicar sucintamente la noción sintáctica de equivalencia lógica. Decimos que dos oraciones Φ y Ψ son «equivalentes» o «lógicamente equivalentes» si (Φ↔Ψ) es un teorema.

9.3 Frases alternativas

En inglés, parece que hay varias frases que suelen tener el mismo significado que el bicondicional. Cada una de las siguientes frases se traduciría como (P↔Q).

P si y sólo si Q.

P por si acaso Q.

P es necesario y suficiente para Q.

P es equivalente a Q.

9.4 Razonamiento con el bicondicional

¿Cómo podemos razonar utilizando un bicondicional? En principio, parecería que ofrece poca orientación. Si sé que (P↔Q), sé que P y Q tienen el mismo valor de verdad, pero sólo a partir de esa frase no sé si ambas son verdaderas o falsas. Sin embargo, podemos aprovechar la semántica del bicondicional para observar que si también conocemos el valor de verdad de una de las oraciones que constituyen el bicondicional, entonces podemos derivar el valor de verdad de la otra oración. Esto sugiere un conjunto sencillo de reglas. En realidad serán cuatro reglas, pero las agruparemos bajo un único nombre, «equivalencia»:

y

y

y

¿Y si en cambio estamos tratando de mostrar un bicondicional? Aquí podemos volver a la idea de que el bicondicional (Φ↔Ψ) es equivalente a ((Φ→Ψ)^(Ψ→Φ)). Si pudiéramos demostrar tanto (Φ→Ψ) como (Ψ→Φ), sabríamos que (Φ↔Ψ) debe ser verdadera.

Podemos llamar a esta regla «bicondición». Tiene la siguiente forma:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Esto significa que a menudo, cuando pretendemos demostrar una bicondición, realizaremos dos derivaciones condicionales para derivar dos condicionales, y luego utilizaremos la regla de la bicondición. Es decir, muchas pruebas de bicondicionales tienen la siguiente forma:

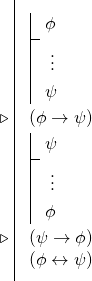
9.5 Volviendo a Hume

Ahora podemos ver si somos capaces de probar el argumento de Hume. Dado ahora el nuevo símbolo bicondicional, podemos empezar una prueba directa con nuestras tres premisas.

Ya hemos observado que pensamos que (QvR) es falso porque ¬Q y ¬R. Así que vamos a demostrar ¬(QvR). Esta frase no se puede demostrar directamente, dadas las premisas que tenemos; y no se puede demostrar con una prueba condicional, ya que no es un condicional. Así que vamos a intentar una prueba indirecta. Creemos que ¬(QvR) es verdadera, así que supondremos la negación de ésta y mostraremos una contradicción.

El argumento de Hume, al menos tal como lo hemos reconstruido, es válido.

¿Es sólido el argumento de Hume? Que sea sólido depende de la primera premisa anterior (ya que la segunda y la tercera son abstracciones sobre algún tema t). Más específicamente, depende de la afirmación de que tenemos conocimiento sobre algo sólo en el caso de que podamos demostrarlo con el experimento o la lógica. Hume sostiene que deberíamos desconfiar -de hecho, deberíamos quemar los textos que contienen- de las afirmaciones que no provienen de la experimentación y la observación, o de la lógica y las matemáticas. Pero consideremos esta afirmación: tenemos conocimiento sobre un tema t si y sólo si nuestras afirmaciones sobre t se aprenden de la experimentación o nuestras afirmaciones sobre t se aprenden de la lógica o las matemáticas.

¿Descubrió Hume esta afirmación a través de experimentos? O la descubrió a través de la lógica? ¿Qué destino sufriría el libro de Hume, si siguiéramos su consejo?

9.6 Algunos ejemplos

Puede ser útil demostrar algunos teoremas que hacen uso del bicondicional, para ilustrar cómo podemos razonar con el bicondicional.

Aquí hay un principio útil. Si dos oraciones tienen el mismo valor de verdad que una tercera oración, entonces tienen el mismo valor de verdad entre sí. Lo afirmamos como (((P↔Q)^(R↔Q))→(P↔R)). Para ilustrar el razonamiento con el bicondicional, demostremos este teorema.

Este teorema es un condicional, por lo que requerirá una derivación condicional. El consecuente del condicional es un bicondicional, por lo que esperaremos necesitar dos derivaciones condicionales, una para demostrar (P→R) y otra para demostrar (R→P). La prueba tendrá el siguiente aspecto. Estúdiala con atención.

Hemos mencionado antes los principios que asociamos con el matemático Augustus De Morgan (1806-1871), y que hoy se llaman «Leyes de De Morgan» o las «Equivalencias de De Morgan». Se trata del reconocimiento de que ¬(PvQ) y (¬P^¬Q) son equivalentes, y también de que ¬(P^Q) y (¬Pv¬Q) son equivalentes. Ahora podemos expresarlas con el bicondicional. Los siguientes son teoremas de nuestra lógica:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

Probaremos el segundo de estos teoremas. Esta es quizás la prueba más difícil que hemos visto; requiere pruebas indirectas anidadas, y una buena cantidad de ingenio para encontrar cuál será la contradicción relevante.

9.7 Uso de teoremas

Cada oración de nuestra lógica es, en términos semánticos, una de tres clases. Es una tautología, una oración contradictoria o una oración contingente. Ya hemos definido la «tautología» (una oración que debe ser verdadera) y la «oración contradictoria» (una oración que debe ser falsa). Una oración contingente es una oración que no es ni una tautología ni una oración contradictoria. Por lo tanto, una oración contingente es una oración que podría ser verdadera, o podría ser falsa.

Aquí hay un ejemplo de cada tipo de oración:

(Pv¬P)

(P↔¬P)

P

La primera es una tautología, la segunda es una oración contradictoria, y la tercera es contingente. Podemos ver esto con una tabla de verdad.

P	P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Nota que la negación de una tautología es una contradicción, la negación de una contradicción es una tautología, y la negación de una oración contingente es una oración contingente.

¬(Pv¬P)

¬(P↔¬P)

¬P

P	¬P	(Pv¬P)	¬(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	T
F	T	T	F	F	T

Un momento de reflexión revelará que sería todo un desastre que una sentencia contradictoria o una sentencia contingente fuera un teorema de nuestra lógica proposicional. Nuestra lógica fue diseñada para producir sólo argumentos válidos. Los argumentos que no tienen premisas, observamos, deben tener conclusiones que deben ser verdaderas (de nuevo, esto se deduce porque una frase que puede demostrarse sin premisas podría demostrarse con cualquier premisa, por lo que es mejor que sea verdadera sin importar las premisas que utilicemos). Si un teorema fuera contradictorio, sabríamos que podemos demostrar una falsedad. Si un teorema fuera contingente, entonces a veces podríamos demostrar una falsedad (es decir, podríamos demostrar una frase que es falsa bajo algunas condiciones). Y, dado que hemos adoptado la derivación indirecta como método de prueba, se deduce que una vez que tenemos una contradicción o una sentencia contradictoria en un argumento, podemos probar cualquier cosa.

Los teoremas pueden sernos muy útiles en los argumentos. Supongamos que sabemos que ni Smith ni Jones irán a Londres, y queremos demostrar, por tanto, que Jones no irá a Londres. Si nos permitimos utilizar uno de los teoremas de De Morgan, podremos hacer un trabajo rápido con el argumento. Supongamos la siguiente clave.

P: Smith irá a Londres.

Q: Jones irá a Londres.

Y tenemos el siguiente argumento:

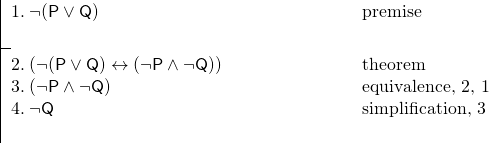
Esta demostración se hizo muy fácil por nuestro uso del teorema en la línea 2.

Hay dos cosas que notar sobre esto. En primer lugar, debemos permitirnos hacer esto, porque si sabemos que una frase es un teorema, entonces sabemos que podríamos demostrar ese teorema en una subprueba. Es decir, podríamos sustituir la línea 2 anterior por una subprueba larga que demuestre (¬(P v Q)↔(¬P ^ ¬Q)), que podríamos utilizar. Pero si estamos seguros de que (¬(P v Q)↔(¬P ^ ¬Q)) es un teorema, no deberíamos necesitar hacer esta prueba una y otra vez, cada vez que queramos hacer uso del teorema.

La segunda cuestión que debemos reconocer es más sutil. Hay infinitas sentencias de la forma de nuestro teorema, y deberíamos poder utilizarlas también. Por ejemplo, las siguientes sentencias tendrían cada una una prueba idéntica a nuestra prueba del teorema (¬(P v Q)↔(¬P ^ ¬Q)), excepto que las letras serían diferentes:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Esto espero que sea obvio. Tomemos la prueba de (¬(P v Q)↔(¬P ^ ¬Q)), y en esa prueba sustituyamos cada instancia de P por R y cada instancia de Q por S, y tendremos una prueba de (¬(R v S)↔(¬R ^ ¬S)).

Pero aquí hay algo que quizás sea menos obvio. Cada una de las siguientes puede considerarse similar al teorema (¬(P v Q)↔(¬P ^ ¬Q)).

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(R→¬Q)))

Por ejemplo, si uno tomara una prueba de (¬(P v Q)↔(¬P ^ ¬Q)) y sustituyera cada instancia inicial de P por (Q↔P) y cada instancia inicial de Q por (¬R→¬Q), entonces se tendría una demostración del teorema (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)).

Podemos captar esta idea de dos maneras. Podríamos enunciar teoremas de nuestro metalenguaje y permitir que éstos tengan instancias. Así, podríamos tomar (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) como un teorema del metalenguaje, en el que podríamos sustituir cada Φ por una sentencia y cada Ψ por una sentencia y obtener una instancia particular de un teorema. Una alternativa es permitir que a partir de un teorema podamos producir otros teoremas mediante la sustitución. Por facilidad, tomaremos esta segunda estrategia.

Nuestra regla será esta. Una vez que demostramos un teorema, podemos citarlo en una demostración en cualquier momento. Nuestra justificación es que la afirmación es un teorema. Permitimos la sustitución de cualquier sentencia atómica en el teorema con cualquier otra sentencia si y sólo si sustituimos cada instancia inicial de esa sentencia atómica en el teorema con la misma sentencia.

Antes de considerar un ejemplo, es beneficioso enumerar algunos teoremas útiles. Hay infinitos teoremas de nuestro lenguaje, pero estos diez son a menudo muy útiles. Algunos los hemos demostrado. Los demás pueden demostrarse como ejercicio.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

Algunos ejemplos dejarán clara la ventaja de usar teoremas. Consideremos un argumento diferente, basado en el anterior. Sabemos que ni es el caso que si Smith va a Londres, irá a Berlín, ni es el caso que si Jones va a Londres irá a Berlín. Queremos demostrar que no se da el caso de que Jones vaya a Berlín. Añadimos lo siguiente a nuestra clave:

R: Smith irá a Berlín.

S: Jones irá a Berlín.

Y tenemos el siguiente argumento:

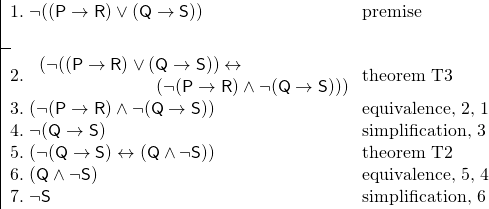
El uso de teoremas ha hecho que esta prueba sea mucho más corta de lo que podría ser de otro modo. Además, los teoremas a menudo hacen que una demostración sea más fácil de seguir, ya que reconocemos los teoremas como tautologías-como oraciones que deben ser verdaderas.

9.8 Problemas

1. Probar que cada uno de los siguientes argumentos es válido.

1. Premisas: P, ¬Q. Conclusión: ¬(P↔Q).
2. Premisas: (¬PvQ), (Pv¬Q). Conclusión: (P↔Q).
3. Premisas: (P↔Q), (R↔S) . Conclusión: ((P^R)↔(Q^S)).

1. Probar cada uno de los siguientes teoremas.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q))
9. ((P→Q)↔¬(P^¬Q))

1. En inglés coloquial normal, escribe tu propio argumento válido con al menos dos premisas, de las cuales al menos una es una bicondicional. Tu argumento debe ser sólo un párrafo (no una lista ordenada de oraciones ni nada que se parezca a la lógica formal). Tradúzcalo a la lógica proposicional y demuestre que es válido.
2. En inglés coloquial normal, escriba su propio argumento válido con al menos dos premisas, y con una conclusión que sea una bicondicional. Tu argumento debe ser sólo un párrafo (no una lista ordenada de oraciones ni nada que parezca formalmente lógico). Tradúzcalo a la lógica proposicional y demuestre que es válido.