Respuesta 7 – 7 – 7 = 73 Se lee «siete al cubo».

Entender los exponentes y las raíces cuadradas

Objetivo(s) de aprendizaje

– Evaluar expresiones que contengan exponentes.

– Escribir factores repetidos utilizando la notación exponencial.

– Encontrar una raíz cuadrada de un cuadrado perfecto.

Los exponentes proporcionan una forma especial de escribir la multiplicación repetida. Los números escritos de esta manera tienen una forma específica, en la que cada parte proporciona información importante sobre el número. Además, escribir los números con exponentes permite ahorrar mucho espacio. La operación inversa a la multiplicación de un número por sí mismo se llama encontrar la raíz cuadrada de un número. Esta operación es útil para problemas sobre el área de un cuadrado.

La notación exponencial es una forma especial de escribir factores repetidos, por ejemplo 7 – 7. La notación exponencial tiene dos partes. Una parte de la notación se llama base. La base es el número que se multiplica por sí mismo. La otra parte de la notación es el exponente, o potencia. Es el número pequeño que se escribe arriba a la derecha de la base. El exponente, o potencia, indica cuántas veces hay que utilizar la base como factor en la multiplicación. En el ejemplo, 7 – 7 puede escribirse como 72, 7 es la base y 2 es el exponente. El exponente 2 significa que hay dos factores.

72 = 7 – 7 = 49

Se puede leer 72 como «siete al cuadrado». Esto es porque multiplicar un número por sí mismo se llama «elevar un número al cuadrado». Del mismo modo, elevar un número a una potencia de 3 se llama «elevar el número al cubo». Puedes leer 73 como «siete al cubo».

Puedes leer 25 como «dos a la quinta potencia» o «dos a la potencia de cinco». Lee 84 como «ocho a la cuarta potencia» u «ocho a la potencia de cuatro». Este formato puede utilizarse para leer cualquier número escrito en notación exponencial. De hecho, aunque 63 se lee más comúnmente como «seis al cubo», también puede leerse como «seis a la tercera potencia» o «seis a la potencia de tres».

Para encontrar el valor de un número escrito en forma exponencial, reescriba el número como una multiplicación repetida y realice la multiplicación. A continuación se muestran dos ejemplos.

Halla el valor de 43.

A) 12

B) 64

C) 256

D) 43

Escribir la multiplicación repetida en notación exponencial puede ahorrar tiempo y espacio. Consideremos el ejemplo 5 – 5 – 5 – 5. Podemos utilizar la notación exponencial para escribir esta multiplicación repetida como 54. Como se está multiplicando 5, se escribe como base. Como la base se utiliza 4 veces en la multiplicación, el exponente es 4. La expresión 5 – 5 – 5 – 5 puede reescribirse en notación exponencial abreviada como 54 y se lee, «cinco a la cuarta potencia» o «cinco a la potencia de 4.»

Para escribir la multiplicación repetida de un mismo número en notación exponencial, primero se escribe el número que se multiplica como base. Luego cuenta cuántas veces se utiliza ese número en la multiplicación y escribe ese número como exponente. Asegúrate de contar los números, no los signos de multiplicación, para determinar el exponente.

Escribe 10 – 10 – 10 – 10 – 10 en notación exponencial.

A) 1.000.000

B) 60

C) 105

D) 106

Como has visto antes, 52 se llama «cinco al cuadrado». «Cinco al cuadrado» significa multiplicar cinco por sí mismo. En matemáticas, llamamos a la multiplicación de un número por sí mismo «elevar al cuadrado» el número. Al resultado de elevar al cuadrado un número entero lo llamamos cuadrado o cuadrado perfecto. Un cuadrado perfecto es cualquier número que puede escribirse como un número entero elevado a la potencia de 2. Por ejemplo, 9 es un cuadrado perfecto. Un número cuadrado perfecto se puede representar como una forma cuadrada, como se muestra a continuación. Vemos que 1, 4, 9, 16, 25 y 36 son ejemplos de cuadrados perfectos.

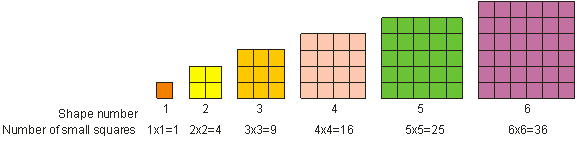
Para elevar al cuadrado un número, multiplícalo por sí mismo. 3 al cuadrado = 32 = 3 – 3 = 9.

Abajo hay más ejemplos de cuadrados perfectos.

La operación inversa de elevar un número al cuadrado se llama hallar la raíz cuadrada de un número. Encontrar una raíz cuadrada es como preguntarse: «¿qué número multiplicado por sí mismo me dará este número?». La raíz cuadrada de 25 es 5, porque 5 multiplicado por sí mismo es igual a 25. Las raíces cuadradas se escriben con un símbolo matemático, llamado signo radical, que tiene este aspecto . La «raíz cuadrada de 25» se escribe .

Encuentra .

A) 6

B) 18

C) 72

D) 7

La notación exponencial es una forma abreviada de escribir la multiplicación repetida de un mismo número. Un número escrito en notación exponencial tiene una base y un exponente, y cada una de estas partes proporciona información para encontrar el valor de la expresión. La base indica qué número se está multiplicando repetidamente, y el exponente indica cuántas veces se utiliza la base en la multiplicación. Los exponentes 2 y 3 tienen nombres especiales. Elevar una base a una potencia de 2 se llama «elevar al cuadrado» un número. Elevar una base a una potencia de 3 se llama «elevar al cubo» un número. La inversa de elevar un número al cuadrado es encontrar la raíz cuadrada de un número. Para encontrar la raíz cuadrada de un número, pregúntate: «¿Qué número puedo multiplicar por sí mismo para obtener este número?»