
La cuestión política: Crédito fiscal para la compra de coches híbridos: ¿es la mejor opción del Gobierno para reducir el consumo de combustible y las emisiones de carbono?
Los habitantes de Estados Unidos y el gobierno están preocupados por la dependencia del petróleo extranjero importado y la emisión de carbono a la atmósfera. En 2005, el Congreso aprobó una ley para ofrecer a los consumidores créditos fiscales para la compra de coches eléctricos e híbridos.
Este crédito fiscal puede parecer una buena opción política, pero es costoso porque reduce directamente la cantidad de ingresos que recauda el Gobierno de Estados Unidos. ¿Existen enfoques más eficaces para reducir la dependencia de los combustibles fósiles y las emisiones de carbono? ¿Cómo decidir cuál es la mejor política? Para responder a esta pregunta, los responsables políticos necesitan predecir con cierta exactitud cómo responderán los consumidores a esta política fiscal antes de que estos responsables gasten millones de dólares federales.
Podemos aplicar el concepto de utilidad a esta cuestión política. En este módulo, estudiaremos la utilidad y las funciones de utilidad. Entonces podremos utilizar una función de utilidad apropiada para derivar curvas de indiferencia que describan nuestra pregunta de política.
Explorando la pregunta de política
Supongamos que el crédito fiscal para subvencionar la compra de coches híbridos tiene un gran éxito y duplica el ahorro medio de combustible de todos los coches que circulan por las carreteras de Estados Unidos, un resultado que claramente no es realista pero que es útil para nuestras discusiones posteriores. ¿Qué crees que pasaría con el consumo de combustible de todos los automovilistas estadounidenses? ¿Debería el gobierno esperar que el consumo de combustible y las emisiones de carbono de los coches disminuyeran a la mitad en respuesta? ¿Por qué o por qué no?
2.1 Funciones de utilidad
LO 2.1: Describir una función de utilidad.
2.2 Funciones de utilidad y preferencias típicas
LO 2.2: Identificar las funciones de utilidad basándose en las preferencias típicas que representan.
2.3 Relacionar las funciones de utilidad y los mapas de curvas de indiferencia
LO 2.3: Explicar cómo derivar una curva de indiferencia a partir de una función de utilidad.
2.4 Hallar la utilidad marginal y la tasa marginal de sustitución
LO 2.4: Derivar la utilidad marginal y la TMS para funciones de utilidad típicas.
2.5. Pregunta de política
2.1 Funciones de utilidad
LO1: Describir una función de utilidad.
Nuestras preferencias nos permiten hacer comparaciones entre distintos paquetes de consumo y elegir los preferidos. Podemos, por ejemplo, determinar la ordenación de un conjunto de paquetes en función de nuestras preferencias. Una función de utilidad es una función matemática que clasifica los paquetes de bienes de consumo asignando un número a cada uno de ellos, donde los números más grandes indican paquetes preferidos. Las funciones de utilidad tienen las propiedades que identificamos en el módulo 1 con respecto a las preferencias. Esto es: son capaces de ordenar los paquetes, son completas y transitivas, se prefiere más a menos y, en casos relevantes, los paquetes mixtos son mejores.
El número que la función de utilidad asigna a un paquete específico se conoce como utilidad, la satisfacción que un consumidor obtiene de un paquete específico. El número de utilidad de cada paquete no significa nada en términos absolutos; no existe una escala uniforme con la que medir la satisfacción. Su único propósito es en términos relativos: podemos utilizar la utilidad para determinar qué paquetes se prefieren a otros.
Si la utilidad del paquete A es mayor que la del paquete B, equivale a decir que un consumidor prefiere el paquete A al paquete B. Las funciones de utilidad, por tanto, clasifican las preferencias de los consumidores asignando un número a cada paquete. . Podemos utilizar una función de utilidad para dibujar los mapas de curvas de indiferencia descritos en el módulo 1. Dado que todos los paquetes de la misma curva de indiferencia proporcionan la misma satisfacción y, por tanto, no se prefiere ninguno, cada paquete tiene la misma utilidad. Por tanto, podemos dibujar una curva de indiferencia determinando todos los paquetes que devuelven el mismo número de la función de utilidad.
Los economistas dicen que las funciones de utilidad son ordinales en lugar de cardinales. Ordinal significa que las funciones de utilidad sólo clasifican los paquetes: sólo indican cuál es mejor, no cuánto mejor es que otro paquete. Supongamos, por ejemplo, que una función de utilidad indica que el paquete A da 10 utilidades y el paquete B 20 utilidades. No decimos que el paquete B sea el doble de bueno o 10 utilidades mejor, sino que el consumidor prefiere el paquete B. Por ejemplo, supongamos que una amiga se presenta a una carrera y nos dice que ha quedado tercera. Esta información es ordinal: Usted sabe que fue más rápida que la cuarta clasificada y más lenta que la segunda. Sólo conoces el orden de llegada de los corredores. Los tiempos individuales son cardinales: Si el primer clasificado corrió la carrera exactamente en una hora y tu amigo terminó en una hora y seis minutos, sabes que tu amigo fue exactamente un 10% más lento que el corredor más rápido. Esto es cierto siempre que se conserve el ordenamiento.
Tomemos por ejemplo la función de utilidad U que describe las preferencias sobre conjuntos de bienes A abd B: U(A,B). Podemos aplicar cualquier transformación monótona positiva a esta función (lo que significa, esencialmente, que no cambiamos el ordenamiento) y la nueva función que hemos creado representará las mismas preferencias. Por ejemplo, podríamos multiplicar una constante positiva, α , o añadir una constante positiva o negativa, β . Así que αU(A,B)+β representa exactamente las mismas preferencias que U(A,B) porque ordenará los paquetes exactamente igual. Este hecho es bastante útil porque a veces aplicar una transformación monótona positiva de una función de utilidad facilita la resolución de problemas.
2.2 Funciones de utilidad y preferencias típicas
LO2: Identificar las funciones de utilidad basándose en las preferencias típicas que representan
Considere los paquetes de manzanas, A, y de plátanos, B. Una función de utilidad que describe las preferencias de Isaac por los paquetes de manzanas y plátanos es la función U(A,B). Pero, ¿cuáles son las preferencias particulares de Isaac por los paquetes de manzanas y plátanos? Supongamos que Isaac tiene unas preferencias bastante estándar por las manzanas y los plátanos que dan lugar a nuestras típicas curvas de indiferencia: Prefiere más a menos y le gusta la variedad. Una función de utilidad que represente estas preferencias podría ser:
U(A,B) = AB
Si las manzanas y los plátanos son complementos perfectos en las preferencias de Isaac, la función de utilidad sería algo así:
U(A,B) = MIN,
donde la función MIN simplemente asigna el menor de los dos números como valor de la función.
Si las manzanas y los plátanos son sustitutos perfectos, la función de utilidad es aditiva y sería algo así:
U(A,B) = A + B
Una clase de funciones de utilidad conocidas como funciones de utilidad Cobb-Douglas se utilizan muy comúnmente en economía por dos razones:
1. Representan las preferencias «bien comportadas», como que más es mejor y la preferencia por la variedad.
2. Son muy flexibles y pueden ajustarse a los datos del mundo real con mucha facilidad.
Las funciones de utilidad Cobb-Douglas tienen esta forma:
U(A,B) = AαBβ
Debido a que las transformaciones monotónicas positivas representan las mismas preferencias, una de estas transformaciones puede utilizarse para establecer α + β = 1 , lo que más adelante veremos que es una condición conveniente que simplifica algunas matemáticas en el problema de elección del consumidor.
Otra forma de transformar la función de utilidad de manera útil es tomar el logaritmo natural de la función, lo que crea una nueva función que tiene el siguiente aspecto:
U(A,B) = αln(A) + βln(B)
Para derivar esta ecuación, basta con aplicar las reglas de los logaritmos naturales. . Es importante tener en cuenta el nivel de abstracción aquí. Normalmente no podemos hacer funciones de utilidad específicas que describan con precisión las preferencias individuales. Probablemente ninguno de nosotros podría describir sus propias preferencias con una sola ecuación. Pero siempre que los consumidores en general tengan preferencias que sigan nuestros supuestos básicos, podemos hacer un buen trabajo encontrando funciones de utilidad que se ajusten a los datos de consumo del mundo real. Veremos pruebas de ello más adelante en el curso.
La tabla 2.1 resume las preferencias y las funciones de utilidad descritas en esta sección.
|
Tabla 2.1 Tipos de preferencias y funciones de utilidad que las representan |
||
|
Preferencias |
Función de utilidad FUNCIÓN |
TIPO DE FUNCIÓN DE UTILIDAD |
|
Amor a la variedad o «buen comportamiento» |
U(A,B) = AB |
Cobb-Douglas |
|
Amor a la Variedad o «Bien Comportado» |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Amor a la variedad o «bien comportado» |
U(A,B) = αln(A) + βln(B) |
Logar natural Cobb-Douglas |
|
Complementos perfectos |
U(A,B) = MIN |
Función Min |
|
Sustituciones Perfectas |
U(A,B) = A + B |
Aditivos |
2.3 Relacionar las funciones de utilidad y los mapas de curvas de indiferencia
LO3: Explicar cómo derivar una curva de indiferencia a partir de una función de utilidad
Las curvas de indiferencia y las funciones de utilidad están directamente relacionadas. De hecho, puesto que las curvas de indiferencia representan las preferencias gráficamente y las funciones de utilidad representan las preferencias matemáticamente, se deduce que las curvas de indiferencia pueden derivarse de las funciones de utilidad.
En las funciones univariantes, la variable dependiente se representa en el eje vertical y la variable independiente se representa en el eje horizontal, como la gráfica de y=f(x). En cambio, las gráficas de las funciones bivariadas son tridimensionales, como U=U(A,B). La figura 2.1 muestra una gráfica de U=A^frac{1}{2}B^frac{1}{2}. Los gráficos tridimensionales son útiles para entender cómo aumenta la utilidad con el aumento del consumo tanto de A como de B.
Figura 2.1 U=A^\frac{1}{2}B^\frac{1}{2}
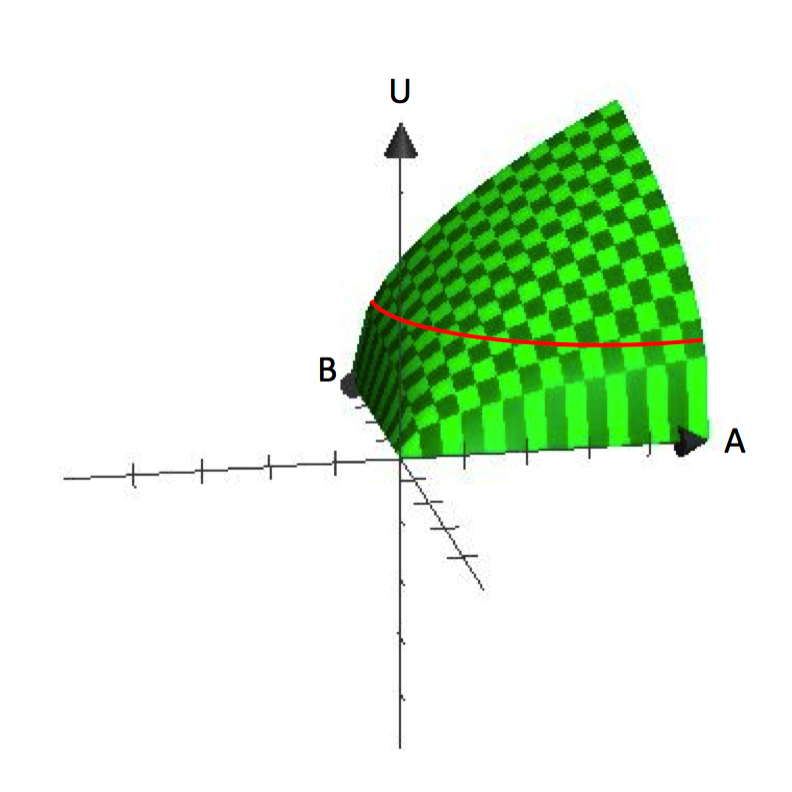
La figura 2.1 muestra claramente el supuesto de que los consumidores tienen preferencia por la variedad. Cada paquete que contiene una cantidad específica de A y B representa un punto en la superficie. La altura vertical de la superficie representa el nivel de utilidad. Aumentando tanto A como B, un consumidor puede alcanzar puntos más altos en la superficie.
¿Entonces de dónde vienen las curvas de indiferencia? Recordemos que una curva de indiferencia es un conjunto de todos los paquetes que a un consumidor le resultan indiferentes, con respecto a cuál consumir. Matemáticamente, esto equivale a decir que todos los paquetes, cuando se ponen en la función de utilidad, devuelven el mismo valor funcional. Así que si fijamos un valor para la utilidad, Ū, y encontramos todos los paquetes de A y B que generan ese valor, definiremos una curva de indiferencia. Observe que esto equivale a encontrar todos los paquetes que llevan al consumidor a la misma altura en la superficie tridimensional de la figura 2.1.
Las curvas de indiferencia son una representación de la elevación (nivel de utilidad) en una superficie plana. En este sentido, son análogas a una línea de contorno en un mapa topográfico. Llevando el gráfico tridimensional al espacio bidimensional -el espacio A, B- podemos mostrar las curvas de nivel/indiferencia que representan diferentes elevaciones o niveles de utilidad. En el gráfico de la figura 2.1, ya se puede ver cómo esta función de utilidad da lugar a curvas de indiferencia «arqueadas» o cóncavas hacia el origen.
Por tanto, las curvas de indiferencia se derivan directamente de las funciones de utilidad y son una forma útil de representar las funciones de utilidad en un gráfico bidimensional.
2.4 Encontrar la utilidad marginal y la tasa marginal de sustitución
LO4: Derivar la utilidad marginal y la TMS para funciones de utilidad típicas.
La utilidad marginal es la utilidad adicional que recibe un consumidor por consumir una unidad adicional de un bien. Matemáticamente lo expresamos como:
MU_{a}=\frac{\Delta \cup }{\Delta A}
o el cambio en la utilidad por un cambio en la cantidad de A consumida, donde Δ representa un cambio en el valor del artículo. Por lo tanto,
MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{{\cup (A+\Delta A,B)-U(A,B)}{\i} {9015>
Nótese que cuando estamos examinando la utilidad marginal del consumo de A, mantenemos B constante.
Utilizando el cálculo, la utilidad marginal es la misma que la derivada parcial de la función de utilidad con respecto a A:
MU_{A} {frac{\a} {parcial U(A,B)} {parcial A}
Consideremos un consumidor que se sienta a comer una comida de ensalada y pizza. Supongamos que mantenemos constante la cantidad de ensalada: una ensalada de acompañamiento con la cena, por ejemplo. Ahora aumentemos las porciones de pizza supongamos que con 1 porción la utilidad es 10, con 2 es 18, con 3 es 24 y con 4 es 28. Representemos estos números en un gráfico que tenga la utilidad en el eje vertical y la pizza en el eje horizontal (Figura 2.2).
Figura 2.2: Gráfico y tabla de la utilidad marginal decreciente
|
Porciones de pizza |
Utilidad |
Marginal Utilidad |
|
1 |
10 |
|
|
2 |
18 |
8 |
|
3 |
24 |
6 |
|
4 |
28 |
4 |
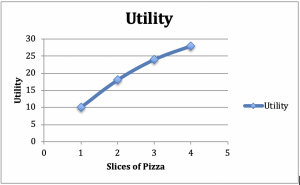
Por la pendiente positiva del gráfico, podemos ver el aumento de la utilidad de las porciones adicionales de pizza. A partir de la forma cóncava del gráfico, podemos ver otro fenómeno común: La utilidad adicional que el consumidor recibe de cada porción adicional de pizza disminuye con el número de porciones consumidas.
El hecho de que la utilidad adicional se hace más pequeña con cada porción adicional de pizza se denomina principio de utilidad marginal decreciente. Este principio se aplica a las preferencias bien comportadas en las que se prefieren los paquetes mixtos.
La tasa marginal de sustitución (TMS) es la cantidad de un bien a la que un consumidor está dispuesto a renunciar para obtener una unidad más de otro bien. Por eso es lo mismo que la pendiente de la curva de indiferencia: como mantenemos constante el nivel de satisfacción, nos mantenemos en la misma curva de indiferencia, sólo que nos movemos a lo largo de ella a medida que cambiamos un bien por otro. La cantidad de uno que está dispuesto a cambiar por uno más de otro depende de la utilidad marginal de cada uno.
Usando nuestro ejemplo anterior, si al consumir una ensalada más de lado su utilidad aumenta en 10, entonces a un consumo actual de 4 porciones de pizza, podría renunciar a 2 porciones de pizza y pasar de 28 a 18 utilidades. 10 utilidades más de la ensalada y 10 utilidades menos al renunciar a 2 porciones de pizza dejan la utilidad general sin cambios, por lo que debemos seguir en la misma curva de indiferencia. A medida que nos movemos a lo largo de la curva de indiferencia, debemos estar montando la pendiente, es decir, debemos estar renunciando al bien en el eje vertical por más del bien en el eje horizontal, lo que produce un aumento negativo sobre un recorrido positivo.
Podemos pasar directamente de la utilidad marginal a la MRS reconociendo la conexión entre los dos conceptos. En nuestro caso, para una función de utilidad U=U(A,B) , la MRS se representa como:
MRS=-\frac{MU_{A}}{MU_{B}}
Nota que al sustituir podemos simplificar la ecuación:
MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{\frac{{Delta U}{Delta A}}{\frac{Delta U}{Delta B}}=-\frac{{Delta B}{Delta A}
Instruyendo el cálculo equivale a:
MRS=-\frac{\frac{parcial U(A,B)}{parcial A}}{\frac{parcial U(A,B)}{parcial B}
2.5 Cuestión de política
Determinamos en el módulo 1 que la decisión relevante del consumidor entre más kilómetros conducidos y otros consumos probablemente se ajusta a los supuestos estándar sobre la elección del consumidor. Por lo tanto, utilizar la función de utilidad Cobb-Douglas para representar a un consumidor al que le gusta conducir un coche además de consumir otros bienes, y que los ve como una compensación (el dinero gastado en gasolina es dinero no gastado en otros bienes de consumo), es una buena elección. Además, tiene las ventajas de ajustarse a los supuestos y de ser flexible:
U(MD,C)=MD^{a}C^{{beta } ,
donde MD = Millas conducidas, y C = Otros consumos.
De hecho, la propia función puede llevarse a datos del mundo real en los que los parámetros y pueden estimarse para este mercado, el de las millas conducidas en el coche del consumidor.
Figura 2.3 Gráfico de curvas de indiferencia para el ejemplo de política
Explorando las preguntas de política:
1 . ¿Serían más apropiados otros tipos de preferencia en este ejemplo?
2. ¿Qué tendría que ser cierto para que los complementos perfectos fueran el tipo de preferencia apropiado para analizar esta política?
¿Qué tendría que ser cierto para los sustitutos perfectos? Dado que estamos considerando un consumidor «típico» que conduce, ¿es apropiado elegir una función de utilidad «típica»?
4. ¿Estamos simplemente adivinando o tenemos alguna base en la teoría para apoyar nuestra elección de las preferencias «bien portadas» o una función de utilidad Cobb-Douglas?
RESUMEN
Revisión: Temas y resultados de aprendizaje relacionados
2.1 Funciones de utilidad
LO 2.1: Describir una función de utilidad
2.2 Funciones de utilidad y preferencias típicas
LO 2.2: Identificar las funciones de utilidad a partir de las preferencias típicas que representan
2.3 Relacionar las funciones de utilidad y los mapas de curvas de indiferencia
LO 2.3: Explicar cómo derivar una curva de indiferencia a partir de una función de utilidad
2.4 Hallar la utilidad marginal y la tasa marginal de sustitución
LO 2.4: Derivar la utilidad marginal y la TMS para funciones de utilidad típicas.
2.5. Pregunta de política
Aprender: Términos clave y gráficos
Bi-funciones variadas
Cardinal
Línea de contorno
Utilidad marginal decreciente
Función
Tasa marginal de sustitución (TMS)
Utilidad marginal
Ordinal
Funciones univariantes
Utilidad
Función de utilidad
Gráficos
Función de utilidad 3D y curva de nivel
Ecuaciones
Cobb-Douglas
Complementos perfectos
Sustitutivos perfectos