En la era moderna del audio, no puedes moverte por la mención de la música «Hi-Res» y la «calidad de estudio» de 24 bits. Si no has detectado la tendencia en los smartphones de gama alta -el códec LDAC Bluetooth de Sony- y en los servicios de streaming como Tidal, entonces tienes que empezar a leer más este sitio.
La promesa es sencilla: una calidad de escucha superior gracias a más datos, también conocida como profundidad de bits. Es decir, 24 bits de unos y ceros digitales frente a los enclenques 16 bits de la era del CD. Por supuesto, habrá que pagar más por estos productos y servicios de mayor calidad, pero seguro que más bits son mejores, ¿no?
El audio de «baja resolución» se muestra a menudo como una forma de onda en escalera. Así no es como funciona el muestreo de audio y no es el aspecto que tiene el audio al salir de un dispositivo.
No necesariamente. La necesidad de profundidades de bits cada vez mayores no se basa en la realidad científica, sino en una tergiversación de la verdad y en la explotación de la falta de conocimiento del consumidor sobre la ciencia del sonido. En última instancia, las empresas que comercializan audio de 24 bits tienen mucho más que ganar en beneficios que en calidad de reproducción superior.
La profundidad de bits y la calidad del sonido: La escalera no es una cosa
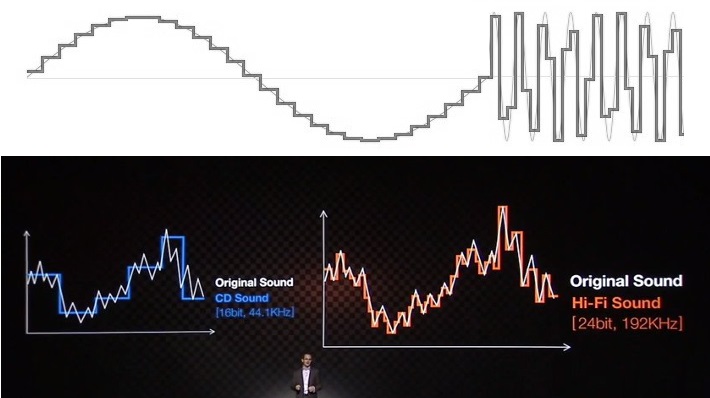
Para sugerir que el audio de 24 bits es imprescindible, las empresas (y demasiadas otras que intentan explicar este tema) sacan a relucir la muy conocida escalera al cielo de la calidad de audio. El ejemplo de los 16 bits siempre muestra una reproducción irregular de una onda sinusoidal u otro tipo de señal, mientras que el equivalente de 24 bits parece maravillosamente suave y de mayor resolución. Es una ayuda visual sencilla, pero que se basa en la ignorancia del tema y de la ciencia para llevar a los consumidores a conclusiones erróneas.
Antes de que alguien me arranque la cabeza, técnicamente hablando estos ejemplos de escalones retratan con cierta precisión el audio en el dominio digital. Sin embargo, un diagrama de tallo/lollipop es un gráfico más preciso para el muestreo visual de audio que estos pasos en escalera. Piénselo de esta manera: una muestra contiene una amplitud en un punto muy específico en el tiempo, no una amplitud mantenida durante una longitud específica de tiempo.

El uso de gráficos escalonados es deliberadamente engañoso cuando los gráficos de tallo proporcionan una representación más precisa del audio digital. Estos dos gráficos trazan los mismos puntos de datos, pero el gráfico en escalera parece mucho menos preciso.
Sin embargo, es correcto que un convertidor analógico-digital (ADC) tiene que encajar una señal de audio analógica infinita en un número finito de bits. Un bit que cae entre dos niveles tiene que ser redondeado a la aproximación más cercana, lo que se conoce como un error de cuantificación o ruido de cuantificación. (Recuerde esto, ya que volveremos a ello.)
Sin embargo, si observa la salida de audio de cualquier convertidor de audio digital a analógico (DAC) construido este siglo (y probablemente mucho antes), no verá ningún escalón. Ni siquiera si emite una señal de 8 bits. Entonces, ¿qué pasa?

Una salida de onda sinusoidal de 8 bits y 10kHz capturada desde un smartphone Pixel 3a de bajo coste. Podemos ver algo de ruido, pero no hay escalones notables tan a menudo retratados por las empresas de audio.
En primer lugar, lo que describen estos diagramas de escalones, si los aplicamos a una salida de audio, es algo llamado DAC de orden cero. Se trata de una tecnología DAC muy simple y barata en la que una señal se conmuta entre varios niveles cada nueva muestra para dar una salida. No se utiliza en ningún producto de audio profesional o de consumo medio decente. Puede que lo encuentres en un microcontrolador de 5 dólares, pero desde luego no en ningún otro sitio. Tergiversar las salidas de audio de esta manera implica una forma de onda distorsionada e inexacta, pero esto no es lo que se obtiene.

En realidad, la salida de un ∆Σ DAC moderno es una señal PDM de 1 bit sobremuestreada (derecha), en lugar de una señal de retención cero (izquierda). Esta última produce una salida analógica de menor ruido cuando se filtra.
Los ADC y DAC de calidad de audio se basan predominantemente en la modulación delta-sigma (∆Σ). Los componentes de este calibre incluyen interpolación y sobremuestreo, conformación de ruido y filtrado para suavizar y reducir el ruido. Los DAC Delta-sigma convierten las muestras de audio en un flujo de 1 bit (modulación de densidad de pulsos) con una frecuencia de muestreo muy alta. Cuando se filtra, se produce una señal de salida suave con el ruido alejado de las frecuencias audibles.
En pocas palabras: los DAC modernos no emiten muestras de audio de aspecto irregular, sino que emiten un flujo de bits filtrado por el ruido en una salida muy precisa y suave. Esta visualización escalonada es errónea debido a algo llamado «ruido de cuantificación»
Entendiendo el ruido de cuantificación
En cualquier sistema finito, se producen errores de redondeo. Es cierto que un ADC o DAC de 24 bits tendrá un error de redondeo menor que un equivalente de 16 bits, pero ¿qué significa eso realmente? Y lo que es más importante, ¿qué es lo que escuchamos realmente? ¿Es distorsión o ruido, se pierden los detalles para siempre?
En realidad es un poco de ambas cosas, dependiendo de si estás en el ámbito digital o analógico. Pero el concepto clave para entender ambos es entender el ruido de fondo y cómo éste mejora a medida que aumenta la profundidad de bits. Para demostrarlo, vamos a dar un paso atrás de los 16 y 24 bits y a ver ejemplos de profundidad de bits muy pequeños.
La diferencia entre las profundidades de 16 y 24 bits no es la precisión en la forma de una onda, sino el límite disponible antes de que el ruido digital interfiera con nuestra señal.
Hay bastantes cosas que comprobar en el ejemplo de abajo, así que primero una rápida explicación de lo que estamos viendo. Tenemos nuestras formas de onda de entrada (azul) y cuantificadas (naranja) en los gráficos superiores, con profundidades de bits de 2, 4 y 8 bits. También hemos añadido una pequeña cantidad de ruido a nuestra señal para simular mejor el mundo real. En la parte inferior, tenemos un gráfico del error de cuantificación o ruido de redondeo, que se calcula restando la señal cuantificada de la señal de entrada.

El ruido de cuantificación aumenta cuanto menor es la profundidad de bits, a través de los errores de redondeo.
El aumento de la profundidad de bits hace claramente que la señal cuantificada coincida mejor con la señal de entrada. Sin embargo, eso no es lo importante, observe la señal de error/ruido mucho mayor para las profundidades de bits más bajas. La señal cuantizada no ha eliminado datos de nuestra entrada, sino que ha añadido esa señal de error. La síntesis aditiva nos dice que una señal puede ser reproducida por la suma de otras dos señales cualquiera, incluyendo las señales desfasadas que actúan como sustracción. Así es como funciona la cancelación del ruido. Así que estos errores de redondeo están introduciendo una nueva señal de ruido.
Esto no es sólo teórico, realmente se puede escuchar más y más ruido en los archivos de audio de menor profundidad de bits. Para entender por qué, examine lo que ocurre en el ejemplo de 2 bits con señales muy pequeñas, como antes de 0,2 segundos. Haga clic aquí para ver un gráfico ampliado. Los cambios muy pequeños en la señal de entrada producen grandes cambios en la versión cuantificada. Este es el error de redondeo en acción, que tiene el efecto de amplificar el ruido de las señales pequeñas. Así que, una vez más, el ruido se hace más fuerte a medida que disminuye la profundidad de bits.
La cuantificación no elimina los datos de nuestra entrada, sino que añade una señal de error ruidosa.
Piensa en esto también a la inversa: no es posible capturar una señal más pequeña que el tamaño del paso de cuantificación, irónicamente conocido como el bit menos significativo. Los pequeños cambios de señal tienen que saltar al nivel de cuantificación más cercano. Las profundidades de bits más grandes tienen pasos de cuantificación más pequeños y, por lo tanto, niveles más pequeños de amplificación de ruido.
Sin embargo, lo más importante es observar que la amplitud del ruido de cuantificación permanece constante, independientemente de la amplitud de las señales de entrada. Esto demuestra que el ruido se produce en todos los diferentes niveles de cuantificación, por lo que hay un nivel de ruido consistente para cualquier profundidad de bits dada. Las mayores profundidades de bits producen menos ruido. Por lo tanto, deberíamos pensar en las diferencias entre las profundidades de 16 y 24 bits no como la precisión en la forma de una onda, sino como el límite disponible antes de que el ruido digital interfiera con nuestra señal.
La profundidad de bits tiene que ver con el ruido
Ahora que hablamos de la profundidad de bits en términos de ruido, volvamos a nuestros gráficos anteriores una última vez. Fíjate en que el ejemplo de 8 bits parece una coincidencia casi perfecta con nuestra señal de entrada ruidosa. Esto se debe a que su resolución de 8 bits es realmente suficiente para capturar el nivel del ruido de fondo. En otras palabras: el tamaño del paso de cuantificación es menor que la amplitud del ruido, o la relación señal-ruido (SNR) es mejor que el nivel de ruido de fondo.
La ecuación 20log(2n), donde n es la profundidad de bits, nos da la SNR. Una señal de 8 bits tiene una SNR de 48dB, la de 12 bits es de 72dB, mientras que la de 16 bits alcanza los 96dB y la de 24 bits la friolera de 144dB. Esto es importante porque ahora sabemos que sólo necesitamos una profundidad de bits con suficiente SNR para acomodar el rango dinámico entre nuestro ruido de fondo y la señal más fuerte que queremos capturar para reproducir el audio tan perfectamente como aparece en el mundo real. Resulta un poco complicado pasar de las escalas relativas del reino digital a las escalas basadas en la presión sonora del mundo físico, así que intentaremos simplificarlo.
Necesitamos una profundidad de bits con suficiente SNR para acomodar nuestro ruido de fondo para capturar nuestro audio tan perfectamente como suena en el mundo real.
Tu oído tiene una sensibilidad que va de 0dB (silencio) a unos 120dB (sonido dolorosamente fuerte), y la capacidad típica de discernir volúmenes es de sólo 1dB de diferencia. Por lo tanto, el rango dinámico de su oído es de unos 120dB, es decir, cerca de 20 bits.
Sin embargo, no puede escuchar todo esto a la vez, ya que la membrana timpánica, o tímpano, se tensa para reducir la cantidad de volumen que realmente llega al oído interno en ambientes ruidosos. Tampoco vas a escuchar música a un volumen tan alto, porque te quedarías sordo. Además, los entornos en los que usted y yo escuchamos música no son tan silenciosos como los oídos sanos pueden escuchar. Un estudio de grabación bien tratado puede llevarnos a menos de 20dB para el ruido de fondo, pero escuchar en un salón bullicioso o en el autobús obviamente empeorará las condiciones y reducirá nuestra necesidad de un rango dinámico alto.
El oído humano tiene un rango dinámico enorme, pero no todo a la vez. El enmascaramiento y la protección auditiva reducen su eficacia.
Además, a medida que aumenta el volumen, el enmascaramiento de las frecuencias más altas surte efecto en el oído. A volúmenes bajos de 20 a 40dB, el enmascaramiento no se produce, excepto para sonidos cercanos en tono. Sin embargo, a 80dB los sonidos por debajo de 40dB se enmascaran, mientras que a 100dB los sonidos por debajo de 70dB son imposibles de escuchar. La naturaleza dinámica del oído y del material de escucha hace que sea difícil dar una cifra precisa, pero el rango dinámico real de tu oído está probablemente en la región de los 70dB en un entorno medio, hasta sólo 40dB en entornos muy ruidosos. Una profundidad de bits de sólo 12 bits probablemente cubriría a la mayoría de la gente, por lo que los CD de 16 bits nos dan mucho margen de maniobra.

hiperfísica El enmascaramiento de las altas frecuencias se produce a volúmenes de escucha elevados, lo que limita nuestra percepción de los sonidos más silenciosos.
La mayoría de los instrumentos y micrófonos de grabación también introducen ruido (especialmente los amplificadores de guitarra), incluso en estudios de grabación muy silenciosos. También se han realizado algunos estudios sobre el rango dinámico de los distintos géneros, incluido éste que muestra un rango dinámico típico de 60dB. Como era de esperar, los géneros con mayor afinidad por las partes silenciosas, como el coro, la ópera y el piano, mostraban rangos dinámicos máximos en torno a los 70dB, mientras que los géneros más «ruidosos» como el rock, el pop y el rap tendían hacia los 60dB o menos. En última instancia, la música sólo se produce y se graba con un límite de fidelidad.
También es posible que esté familiarizado con las «guerras de sonoridad» de la industria musical, lo que ciertamente anula el propósito de los formatos de audio de alta resolución actuales. El uso intensivo de la compresión (que aumenta el ruido y atenúa los picos) reduce el rango dinámico. La música moderna tiene un rango dinámico considerablemente menor que los álbumes de hace 30 años. En teoría, la música moderna podría distribuirse con tasas de bits más bajas que la antigua. Puede comprobar el rango dinámico de una serie de álbumes aquí.

La calidad de un CD puede ser «sólo» de 16 bits, pero es excesiva para la calidad.
16 bits es todo lo que necesita
Esto ha sido todo un viaje, pero esperamos que haya salido con una imagen mucho más matizada de la profundidad de bits, el ruido y el rango dinámico, que esos engañosos ejemplos en escalera que se ven tan a menudo.
La profundidad de bits tiene que ver con el ruido, y cuantos más bits de datos tengas para almacenar el audio, menos ruido de cuantificación se introducirá en tu grabación. Por la misma razón, también podrás capturar señales más pequeñas con mayor precisión, lo que ayudará a conducir el piso de ruido digital por debajo de la grabación o el entorno de escucha. Eso es todo lo que necesitamos de la profundidad de bits. No hay ninguna ventaja en utilizar profundidades de bits enormes para los masters de audio.
Sorprendentemente, 12 bits es probablemente suficiente para un master de música con un sonido decente y para atender el rango dinámico de la mayoría de los entornos de escucha. Sin embargo, el audio digital no sólo transporta música, y ejemplos como el habla o las grabaciones ambientales para la televisión pueden hacer uso de un rango dinámico más amplio que la mayoría de la música. Además, un poco de espacio para la separación entre el volumen y el silencio no hace daño a nadie.
En general, los 16 bits (96dB de rango dinámico o 120dB con dithering aplicado) se adaptan a una amplia gama de tipos de audio, así como a los límites de la audición humana y los entornos de escucha típicos. Los aumentos perceptivos de la calidad de 24 bits son muy discutibles, si no simplemente un placebo, como espero haber demostrado. Además, el aumento del tamaño de los archivos y del ancho de banda los hace innecesarios. El tipo de compresión utilizado para reducir el tamaño de los archivos de la biblioteca musical o de la transmisión tiene un impacto mucho más notable en la calidad del sonido que el hecho de que se trate de un archivo de 16 o 24 bits.