En esta lección, mostraremos una estrategia fácil para resolver el siguiente problema: cómo hallar el área de un triángulo isósceles.
Pongamos en práctica varias de las propiedades que hemos demostrado hasta ahora, en el siguiente problema de geometría:
Problema
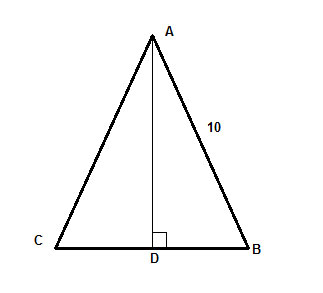
En un triángulo isósceles, ΔABC, con longitud de cateto 10, la altura a la base es igual a dos tercios de la base. Halla el área del triángulo.
Estrategia
Para resolver este problema, trabajaremos al revés de lo que tenemos que hacer.
Necesitamos encontrar el área del triángulo que sabemos que viene dada por la fórmula (base por altura)/2.
Un problema que tenemos es que no conocemos ni la longitud de la base ni la altura. Pero, nos dan la relación entre ellas, que es la pista de lo que tenemos que hacer. Llamemos a la longitud de la base, BC, x.
Entonces sabemos que la altura, AD, es 2x/3, como se da en el problema.
Así que la respuesta que buscamos es (base por altura)/2, o x por 2x/3, dividido por dos.
¿Pero cómo encontramos x? Hay dos cosas adicionales que nos dieron en el problema y que aún no hemos utilizado: la longitud del cateto (10), y el hecho de que se trata de un triángulo isósceles. Probablemente necesitemos usar estas dos cosas para resolver el problema.
Revisemos las propiedades de los triángulos isósceles. Una cosa que debe saltar inmediatamente a la mente es que, como hemos demostrado, en un triángulo isósceles, la altura a la base biseca la base, por lo que CD=DB=x/2.
Por último, AD es la altura, lo que significa que el ángulo ∠ADC es un ángulo recto, y tenemos un triángulo rectángulo, ΔADC, cuya hipotenusa conocemos (10) y podemos usar para hallar los catetos usando el teorema de Pitágoras, c2 =a2+b2,
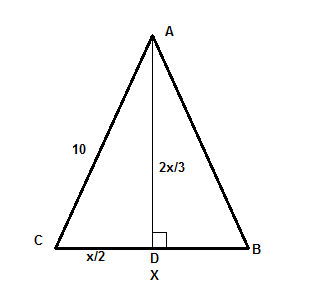
donde c= 10 ,a = x/2 y b=2x/3 . Y ya hemos terminado, el resto es sólo resolver algebraicamente para x.
Prueba: área de un triángulo isósceles
(1) ΔADC es triángulo rectángulo //dado, ya que AD es la altura a la base
(2) AC2 =CD2 + AD2 //Teorema de Pitágoras
(3) AC= 10 //dado
(4) CB = x
(5) CD = x/2 //La altura a la base en el triángulo isósceles biseca la base
(6) AD = 2x/3 //dado
(7) 102 = (x/2)2 + (2x/3)2 //Sustituir en (2)
(8) 100 = x2/4+4×2/9 //simplificar
(9) 100*36 = 9×2 +16×2 //multiplicar ambos lados por 36
(10) 100*36 = 25×2 //reunir términos similares