La desviación estándar es la cantidad media de variabilidad en su conjunto de datos. Le dice, en promedio, qué tan lejos está cada valor de la media.
Una desviación estándar alta significa que los valores están generalmente lejos de la media, mientras que una desviación estándar baja indica que los valores se agrupan cerca de la media.
¿Qué le dice la desviación estándar?
La desviación estándar es una medida útil de dispersión para las distribuciones normales.
En las distribuciones normales, los datos se distribuyen simétricamente sin sesgo. La mayoría de los valores se agrupan alrededor de una región central, y los valores disminuyen a medida que se alejan del centro. La desviación estándar le indica cuán alejados del centro de la distribución están sus datos en promedio.
Muchas variables científicas siguen distribuciones normales, incluyendo la estatura, las calificaciones estandarizadas de los exámenes o las calificaciones de satisfacción laboral. Cuando tienes las desviaciones estándar de diferentes muestras, puedes comparar sus distribuciones utilizando pruebas estadísticas para hacer inferencias sobre las poblaciones más grandes de las que provienen.
Las valoraciones medias (M) son las mismas para cada grupo: es el valor en el eje x cuando la curva está en su punto máximo. Sin embargo, sus desviaciones estándar (SD) difieren entre sí.
La desviación estándar refleja la dispersión de la distribución. La curva con la menor desviación estándar tiene un pico alto y una pequeña dispersión, mientras que la curva con la mayor desviación estándar es más plana y extendida.
La regla empírica
La desviación estándar y la media juntas pueden indicarle dónde se encuentra la mayoría de los valores de su distribución si siguen una distribución normal.
La regla empírica, o la regla del 68-95-99,7, le indica dónde se encuentran sus valores:
- Alrededor del 68% de las puntuaciones están dentro de 2 desviaciones estándar de la media,
- Alrededor del 95% de las puntuaciones están dentro de 4 desviaciones estándar de la media,
- Alrededor del 99.El 7% de las puntuaciones están dentro de las 6 desviaciones estándar de la media.
Siguiendo la regla empírica:
- Alrededor del 68% de las puntuaciones están entre 40 y 60.
- Alrededor del 95% de las puntuaciones están entre 30 y 70.
- Alrededor del 99,7% de las puntuaciones están entre 20 y 80.
La regla empírica es una forma rápida de obtener una visión general de sus datos y comprobar si hay valores atípicos o extremos que no siguen este patrón.
Para las distribuciones no normales, la desviación estándar es una medida menos fiable de la variabilidad y debe utilizarse en combinación con otras medidas como el rango o el rango intercuartílico.
Fórmulas de desviación estándar para poblaciones y muestras
Se utilizan diferentes fórmulas para calcular las desviaciones estándar dependiendo de si se tienen datos de una población completa o de una muestra.
Desviación típica de la población
Cuando se han recogido datos de todos los miembros de la población que interesa, se puede obtener un valor exacto de la desviación típica de la población.
La fórmula de la desviación estándar de la población tiene el siguiente aspecto:
| Fórmula | Explicación |
|---|---|
 |
|
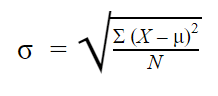Desviación típica de la muestra
Cuando se recogen datos de una muestra, la desviación típica de la muestra se utiliza para hacer estimaciones o inferencias sobre la desviación típica de la población.
La fórmula de la desviación estándar de la muestra tiene el siguiente aspecto:
| Fórmula | Explicación |
|---|---|
 |
|
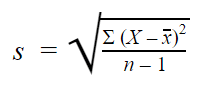Con las muestras, utilizamos n – 1 en la fórmula porque utilizar n nos daría una estimación sesgada que subestima sistemáticamente la variabilidad. La desviación estándar de la muestra tendería a ser menor que la desviación estándar real de la población.
Reducir la muestra n a n – 1 hace que la desviación estándar sea artificialmente grande, dándole una estimación conservadora de la variabilidad.
Si bien esto no es una estimación insesgada, es una estimación menos sesgada de la desviación estándar: es mejor sobreestimar que subestimar la variabilidad en las muestras.
Pasos para calcular la desviación estándar
La desviación estándar suele ser calculada automáticamente por cualquier software que utilices para tu análisis estadístico. Pero también puedes calcularla a mano para entender mejor cómo funciona la fórmula.
Hay seis pasos principales para encontrar la desviación estándar a mano. Utilizaremos un pequeño conjunto de datos de 6 puntuaciones para recorrer los pasos.
| Conjunto de datos | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 52 | 41 | |
Paso 1: Hallar la media
Para hallar la media, sume todas las puntuaciones y luego divídalas por el número de puntuaciones.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Paso 2: Hallar la desviación de cada puntuación respecto a la media
Restar la media de cada puntuación para obtener las desviaciones respecto a la media.
Dado que x̅ = 50, aquí restamos 50 a cada puntuación.
| Puntuación | Desviación de la media |
|---|---|
| 46 | 46 – 50 = -.4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Paso 3: Eleva al cuadrado cada desviación de la media
Multiplica cada desviación de la media por sí misma. Esto dará como resultado números positivos.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
Paso 4: Halla la suma de cuadrados
Suma todas las desviaciones al cuadrado. Esto se llama suma de cuadrados.
16 + 361 + 324 + 100 + 4 + 81 = 886
Paso 5: Hallar la varianza
Dividir la suma de los cuadrados por n – 1 (para una muestra) o N (para una población) – esto es la varianza.
Como estamos trabajando con un tamaño de muestra de 6, utilizaremos n – 1, donde n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
Paso 6: Hallar la raíz cuadrada de la varianza
Para hallar la desviación típica, tomamos la raíz cuadrada de la varianza.
√177,2 = 13,31
Desde que aprendemos que SD = 13.31, podemos decir que cada puntuación se desvía de la media en 13,31 puntos de media.
¿Por qué la desviación estándar es una medida útil de la variabilidad?
Aunque hay formas más sencillas de calcular la variabilidad, la fórmula de la desviación estándar pondera más las muestras desiguales que las uniformes. Una desviación estándar más alta le indica que la distribución no sólo está más extendida, sino que también está más desigualmente extendida.
Esto significa que le da una mejor idea de la variabilidad de sus datos que otras medidas más simples, como la desviación media absoluta (DMA).
La DMA es similar a la desviación estándar pero más fácil de calcular. Primero, se expresa cada desviación de la media en valores absolutos convirtiéndolos en números positivos (por ejemplo, -3 se convierte en 3). Luego, se calcula la media de estas desviaciones absolutas.
A diferencia de la desviación estándar, para la DAM no hay que calcular cuadrados o raíces cuadradas de números. Sin embargo, por esa razón, le da una medida menos precisa de la variabilidad.
Tomemos dos muestras con la misma tendencia central pero con diferentes cantidades de variabilidad. La muestra B es más variable que la muestra A.
| Valores | Media | Desviación absoluta media | Desviación estándar | |
|---|---|---|---|---|
| Muestra A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| Muestra B | 51, 21, 79, 49 | 50 | 15 | 23,7 |
Para muestras con desviaciones medias iguales respecto a la media, la MAD no puede diferenciar niveles de dispersión. La desviación estándar es más precisa: es mayor para la muestra con más variabilidad en las desviaciones respecto a la media.
Al elevar al cuadrado las diferencias respecto a la media, la desviación estándar refleja la dispersión desigual con mayor precisión. Este paso pondera más las desviaciones extremas que las pequeñas.
Sin embargo, esto también hace que la desviación estándar sea sensible a los valores atípicos.
Preguntas frecuentes sobre la desviación estándar
La variabilidad se mide más comúnmente con los siguientes estadísticos descriptivos:
- Rango: la diferencia entre los valores más altos y más bajos
- Rango intercuartil: el rango de la mitad media de una distribución
- Desviación estándar: distancia media a la media
- Varianza: media de las distancias al cuadrado de la media
La desviación estándar es la cantidad media de variabilidad en tu conjunto de datos. Te dice, en promedio, qué tan lejos está cada puntuación de la media.
En las distribuciones normales, una desviación estándar alta significa que los valores están generalmente lejos de la media, mientras que una desviación estándar baja indica que los valores están agrupados cerca de la media.
En una distribución normal, los datos se distribuyen de forma simétrica y sin sesgo. La mayoría de los valores se agrupan alrededor de una región central, y los valores disminuyen a medida que se alejan del centro.
Las medidas de tendencia central (media, moda y mediana) son exactamente las mismas en una distribución normal.
La regla empírica, o la regla del 68-95-99,7, indica dónde se encuentra la mayoría de los valores en una distribución normal:
- Alrededor del 68% de los valores están dentro de una desviación estándar de la media.
- Alrededor del 95% de los valores están dentro de 2 desviaciones estándar de la media.
- Alrededor del 99.El 7% de los valores están dentro de 3 desviaciones estándar de la media.
La regla empírica es una forma rápida de obtener una visión general de sus datos y comprobar si hay valores atípicos o extremos que no siguen este patrón.
La varianza es la media de las desviaciones al cuadrado de la media, mientras que la desviación estándar es la raíz cuadrada de este número. Ambas medidas reflejan la variabilidad en una distribución, pero sus unidades difieren:
- La desviación estándar se expresa en las mismas unidades que los valores originales (por ejemplo, minutos o metros).
- La varianza se expresa en unidades mucho mayores (por ejemplo, metros al cuadrado).
Aunque las unidades de la varianza son más difíciles de entender intuitivamente, la varianza es importante en las pruebas estadísticas.