MesopotámicoEditar
El período 2700-2300 a.C. vio la primera aparición del ábaco sumerio, una tabla de columnas sucesivas que delimitaba los sucesivos órdenes de magnitud de su sistema numérico sexagesimal.
Algunos estudiosos señalan un carácter en el cuneiforme babilónico que puede haber derivado de una representación del ábaco. Los estudiosos de la antigua Babilonia, como Carruccio, creen que los antiguos babilonios «pueden haber utilizado el ábaco para las operaciones de adición y sustracción; sin embargo, este dispositivo primitivo resultó difícil de utilizar para cálculos más complejos».
EgiptoEditar
El uso del ábaco en el Antiguo Egipto es mencionado por el historiador griego Heródoto, quien escribe que los egipcios manipulaban los guijarros de derecha a izquierda, en sentido contrario al método griego de izquierda a derecha. Los arqueólogos han encontrado antiguos discos de varios tamaños que se cree que se utilizaban como contadores. Sin embargo, no se han descubierto representaciones murales de este instrumento.
PersaEditar
Durante el Imperio Aqueménida, alrededor del año 600 a.C. los persas comenzaron a utilizar el ábaco. Bajo los imperios parto, sasánida e iraní, los eruditos se concentraron en el intercambio de conocimientos e inventos con los países de su entorno: India, China y el Imperio Romano, cuando se cree que se exportó a otros países.
GreekEdit
Las primeras evidencias arqueológicas del uso del ábaco griego datan del siglo V a.C. También Demóstenes (384 a.C.-322 a.C.) hablaba de la necesidad de utilizar guijarros para los cálculos demasiado difíciles para la cabeza. Una obra de Alexis del siglo IV a.C. menciona un ábaco y guijarros para hacer cuentas, y tanto Diógenes como Polibio mencionan hombres que a veces representaban más y a veces menos, como los guijarros de un ábaco. El ábaco griego era una mesa de madera o mármol, provista de pequeñas fichas de madera o metal para realizar cálculos matemáticos. Este ábaco griego se utilizó en la Persia aqueménida, en la civilización etrusca, en la antigua Roma y, hasta la Revolución Francesa, en el mundo cristiano occidental.
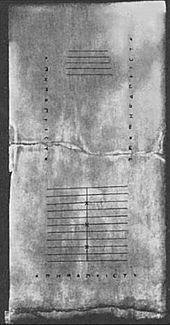
Una tablilla encontrada en la isla griega de Salamina en 1846 d.C. (la Tablilla de Salamina), data del año 300 a.C., lo que la convierte en la tabla de contar más antigua descubierta hasta ahora. Se trata de una losa de mármol blanco de 149 cm de largo, 75 cm de ancho y 4,5 cm de grosor, en la que hay 5 grupos de marcas. En el centro de la lápida hay un conjunto de 5 líneas paralelas divididas a partes iguales por una línea vertical, rematadas con un semicírculo en la intersección de la línea horizontal más inferior y la única línea vertical. Debajo de estas líneas hay un amplio espacio con una grieta horizontal que lo divide. Debajo de esta grieta hay otro grupo de once líneas paralelas, de nuevo divididas en dos secciones por una línea perpendicular a ellas, pero con el semicírculo en la parte superior de la intersección; la tercera, la sexta y la novena de estas líneas están marcadas con una cruz donde se cruzan con la línea vertical. También de esta época es el jarrón de Darío, desenterrado en 1851. Estaba cubierto con imágenes que incluían a un «tesorero» que sostenía una tablilla de cera en una mano mientras manipulaba fichas en una mesa con la otra.
ChineseEdit

| Abaco | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chino tradicional | 算盤 | |||||||||||||||
| Chino simplificado | 算盘 | |||||||||||||||
| Literal significado | «bandeja de cálculo» | |||||||||||||||
| Transcripciones | Mandarín estándar | Hanyu Pinyin | IPA | Yue: Cantonés | Ranización Yale | Jyutping | IPA | Southern Min | Hokkien POJ | Tâi-lô | ||||||
La primera documentación escrita conocida del ábaco chino data del siglo II a.C.
El ábaco chino, conocido como suanpan (算盤/算盘, lit. «bandeja de cálculo»), suele tener una altura de 20 cm (8 pulgadas) y se presenta en varias anchuras dependiendo del operador. Suele tener más de siete varillas. Hay dos cuentas en cada varilla en el piso superior y cinco cuentas en el inferior. Las cuentas suelen ser redondeadas y de madera dura. Las cuentas se cuentan moviéndolas hacia arriba o hacia abajo en dirección a la viga; las cuentas que se mueven hacia la viga se cuentan, mientras que las que se alejan de ella no se cuentan. Una de las cuentas superiores es el 5, mientras que una de las cuentas inferiores es el 1. Cada varilla tiene un número debajo, mostrando el valor del lugar.El suanpan puede volver a la posición inicial instantáneamente mediante un movimiento rápido a lo largo del eje horizontal para girar todas las cuentas lejos de la viga horizontal en el centro.
El prototipo del ábaco chino apareció durante la dinastía Han, y las cuentas son ovaladas. La dinastía Song y anteriores utilizaron el tipo 1:4 o ábaco de cuatro cuentas similar al ábaco moderno, incluyendo la forma de las cuentas comúnmente conocida como ábaco de estilo japonés.
A principios de la dinastía Ming, el ábaco comenzó a aparecer en forma de ábaco 1:5. El piso superior tenía una cuenta y el inferior cinco.
A finales de la dinastía Ming, los estilos de ábaco aparecieron en forma de 2:5. El piso superior tenía dos cuentas y el inferior cinco. La cubierta superior tenía dos cuentas y la inferior cinco.
Se idearon diversas técnicas de cálculo para el Suanpan que permitían realizar cálculos eficientes. Actualmente hay escuelas que enseñan a los estudiantes a utilizarlo.
En el largo pergamino A lo largo del río durante el festival Qingming, pintado por Zhang Zeduan durante la dinastía Song (960-1297), se ve claramente un suanpan junto a un libro de cuentas y recetas médicas en el mostrador de una botica (Feibao).
La similitud del ábaco romano con el chino sugiere que uno podría haber inspirado al otro, ya que existen pruebas de una relación comercial entre el Imperio Romano y China. Sin embargo, no se puede demostrar ninguna conexión directa, y la similitud de los ábacos puede ser una coincidencia, ya que ambos surgen en última instancia de contar con cinco dedos por mano. Mientras que el modelo romano (como la mayoría de los coreanos y japoneses modernos) tiene 4 más una cuenta por decimal, el suanpan estándar tiene 5 más 2. Por cierto, esto permite el uso con un sistema numérico hexadecimal (o cualquier base hasta 18) que puede haber sido utilizado para las medidas tradicionales chinas de peso. (En lugar de funcionar con cables como en los modelos chinos, coreanos y japoneses, las cuentas del modelo romano funcionan en ranuras, lo que presumiblemente hace que los cálculos aritméticos sean mucho más lentos.
Otra posible fuente del suanpan son las varillas contadoras chinas, que funcionaban con un sistema decimal pero carecían del concepto de cero como marcador de posición. El cero fue probablemente introducido en los chinos en la dinastía Tang (618-907), cuando los viajes por el océano Índico y Oriente Medio habrían proporcionado un contacto directo con la India, lo que les permitió adquirir el concepto de cero y el punto decimal de los comerciantes y matemáticos indios.
Abaco romano

El método normal de cálculo en la antigua Roma, al igual que en Grecia, consistía en mover fichas sobre una mesa lisa. Originalmente se utilizaban guijarros (calculi). Más tarde, y en la Europa medieval, se fabricaron jetones. Las líneas marcadas indicaban las unidades, cincos, decenas, etc., como en el sistema numérico romano. Este sistema de «contrafacturación» continuó en el imperio romano tardío y en la Europa medieval, y persistió en uso limitado hasta el siglo XIX. Debido a la reintroducción del ábaco con modificaciones por parte del Papa Silvestre II, se volvió a utilizar ampliamente en Europa durante el siglo XI. Este ábaco utilizaba cuentas en hilos, a diferencia de las tradicionales tablas de contar romanas, lo que significaba que el ábaco podía utilizarse mucho más rápido.
Escribiendo en el siglo I a.C., Horacio se refiere al ábaco de cera, un tablero cubierto con una fina capa de cera negra en el que se inscribían columnas y cifras con un estilete.
Un ejemplo de evidencia arqueológica del ábaco romano, mostrado aquí en reconstrucción, data del siglo I d.C. Tiene ocho ranuras largas con hasta cinco cuentas en cada una y ocho ranuras más cortas con una o ninguna cuenta en cada una. La ranura marcada con la I indica unidades, la X decenas, y así sucesivamente hasta millones. Las cuentas de las ranuras más cortas indican cinco unidades, cinco decenas, etc., esencialmente en un sistema decimal codificado bicuadrado, relacionado con los números romanos. Las ranuras cortas de la derecha pueden haber sido utilizadas para marcar «onzas» romanas (es decir, fracciones).
IndianEdit
El Abhidharmakośabhāṣya de Vasubandhu (316-396), una obra sánscrita de filosofía budista, dice que el filósofo del siglo II de nuestra era Vasumitra dijo que «colocar una mecha (sánscrito vartikā) sobre el número uno (ekāṅka) significa que es un uno, mientras que colocar la mecha sobre el número cien significa que se llama cien, y sobre el número mil significa que es un mil». No está claro en qué consistía exactamente esta disposición. Alrededor del siglo V, los oficinistas indios ya encontraban nuevas formas de registrar el contenido del ábaco. Los textos hindúes utilizaban el término śūnya (cero) para indicar la columna vacía del ábaco.
JaponésEdit

En japonés, el ábaco se llama soroban (算盤, そろばん, lit. «Bandeja para contar»), importado de China en el siglo XIV. Probablemente fue utilizado por la clase trabajadora un siglo o más antes de que lo hiciera la clase dirigente, ya que la estructura de clases no permitía que los dispositivos utilizados por la clase baja fueran adoptados o utilizados por la clase dirigente. El ábaco de 1/4, que elimina la segunda y la quinta cuenta poco utilizadas, se hizo popular en la década de 1940.
El ábaco japonés actual es del tipo 1:4, el ábaco de cuatro cuentas fue introducido desde China en la era Muromachi. Adopta la forma de una cuenta en el piso superior y cuatro en el inferior. La cuenta superior del piso superior era igual a cinco y la inferior es igual a uno como el ábaco chino o coreano, y se puede expresar el número decimal, por lo que el ábaco está diseñado como un ábaco de cuatro. Las cuentas tienen siempre forma de diamante. La división del cociente se utiliza generalmente en lugar del método de la división; al mismo tiempo, para que los dígitos de la multiplicación y la división sean coherentes, se utiliza la multiplicación de la división. Más tarde, Japón tuvo un ábaco de tipo 3:5 llamado 天三算盤, que ahora es la colección Ize Rongji del pueblo de Shansi en la ciudad de Yamagata. También había ábacos del tipo 2:5.
Con la difusión del ábaco de cuatro cuentas, también es común el uso del ábaco japonés en todo el mundo. También hay ábacos japoneses mejorados en varios lugares. Uno de los ábacos japoneses fabricados en China es un ábaco de cuentas de plástico con marco de aluminio. La lima está al lado de las cuatro cuentas, y el botón de «compensación», presiona el botón de compensación, inmediatamente pone la cuenta superior a la posición superior, la cuenta inferior se marca a la posición inferior, inmediatamente la compensación, fácil de usar.
El ábaco se sigue fabricando en Japón hoy en día, incluso con la proliferación, la practicidad, y la asequibilidad de las calculadoras electrónicas de bolsillo. El uso del sorobán se sigue enseñando en las escuelas primarias japonesas como parte de las matemáticas, principalmente como ayuda para un cálculo mental más rápido. Utilizando la imagen visual de un soroban, se puede llegar a la respuesta en el mismo tiempo, o incluso más rápido, que es posible con un instrumento físico.
KoreanEdit
El ábaco chino emigró de China a Corea alrededor del año 1400 DC. Los coreanos lo llaman jupan (주판), supan (수판) o jusan (주산).El ábaco de cuatro cuentas( 1:4 ) fue introducido en Corea Dinastía Goryeo desde la China durante la Dinastía Song, más tarde el ábaco de cinco cuentas (5:1) fue introducido en Corea desde China durante la Dinastía Ming.
Nativos americanosEditar


Algunas fuentes mencionan el uso de un ábaco llamado nepohualtzintzin en la antigua cultura azteca. Este ábaco mesoamericano utilizaba un sistema de 5 dígitos de base 20.La palabra Nepōhualtzintzin proviene del náhuatl y está formada por las raíces; Ne – personal -; pōhual o pōhualli – la cuenta -; y tzintzin – pequeños elementos similares. Su significado completo fue tomado como: contar con pequeños elementos similares por alguien. Su uso se enseñaba en el Calmecac a los temalpouhqueh , que eran alumnos dedicados a llevar las cuentas de los cielos, desde la infancia.
El Nepōhualtzintzin estaba dividido en dos partes principales separadas por una barra o cordón intermedio. En la parte izquierda había cuatro cuentas, que en la primera fila tienen valores unitarios (1, 2, 3 y 4), y en la parte derecha hay tres cuentas con valores de 5, 10 y 15 respectivamente. Para conocer el valor de las respectivas cuentas de las filas superiores, basta con multiplicar por 20 (por cada fila), el valor de la cuenta correspondiente en la primera fila.
En total, había 13 filas con 7 cuentas en cada una, que conformaban 91 cuentas en cada Nepōhualtzintzin. Este era un número básico para entender, 7 veces 13, una estrecha relación concebida entre los fenómenos naturales, el inframundo y los ciclos de los cielos. Un Nepōhualtzintzin (91) representaba el número de días que dura una estación del año, dos Nepōhualtzitzin (182) es el número de días del ciclo del maíz, desde su siembra hasta su cosecha, tres Nepōhualtzintzin (273) es el número de días de la gestación de un bebé, y cuatro Nepōhualtzintzin (364) completaban un ciclo y se aproximaban a un año (11/4 días menos). Traducido a la aritmética informática moderna, el Nepōhualtzintzin equivalía al rango del 10 al 18 en coma flotante, que calculaba con precisión absoluta tanto las cantidades estelares como las infinitesimales, lo que significaba que no se permitía el redondeo.
El redescubrimiento del Nepōhualtzintzin se debió al ingeniero mexicano David Esparza Hidalgo, quien en sus andanzas por México encontró diversos grabados y pinturas de este instrumento y reconstruyó varios de ellos realizados en oro, jade, incrustaciones de concha, etc. También se han encontrado Nepōhualtzintzin muy antiguos atribuidos a la cultura olmeca, e incluso algunos brazaletes de origen maya, así como una diversidad de formas y materiales en otras culturas.
George I. Sánchez, «Arithmetic in Maya», Austin-Texas, 1961 encontró otro ábaco de base 5, base 4 en la Península de Yucatán que también calculaba datos del calendario. Este era un ábaco de dedos, por un lado se usaban 0, 1, 2, 3 y 4; y por otro lado se usaban 0, 1, 2 y 3. Nótese el uso del cero al principio y al final de los dos ciclos. Sánchez trabajó con Sylvanus Morley, un destacado mayista.
El quipu de los incas era un sistema de cuerdas anudadas de colores que se utilizaba para registrar datos numéricos, como palos de conteo avanzados – pero no se utilizaba para realizar cálculos. Los cálculos se realizaban con una yupana (herramienta de recuento en quechua; véase la figura) que seguía utilizándose tras la conquista de Perú. El principio de funcionamiento de una yupana es desconocido, pero en 2001 el matemático italiano Nicolino De Pasquale propuso una explicación de la base matemática de estos instrumentos. Comparando la forma de varias yupanas, los investigadores descubrieron que los cálculos se basaban en la secuencia de Fibonacci 1, 1, 2, 3, 5 y potencias de 10, 20 y 40 como valores de posición para los diferentes campos del instrumento. El uso de la secuencia de Fibonacci mantendría el número de granos dentro de cualquier campo al mínimo.
RussianEdit

El ábaco ruso, el schoty (ruso: счёты, plural del ruso: счёт, contar), suele tener una sola pletina inclinada, con diez cuentas en cada hilo (excepto un hilo, normalmente colocado cerca del usuario, con cuatro cuentas para las fracciones de cuarto de rublo). Los modelos más antiguos tienen otro hilo con cuatro cuentas para los cuartos de rublo, que se acuñaron hasta 1916. El ábaco ruso se suele utilizar en vertical, con cada hilo de izquierda a derecha como las líneas de un libro. Los alambres suelen doblarse para abultarse hacia arriba en el centro, para mantener las cuentas clavadas en cualquiera de los dos lados. Se despeja cuando todas las cuentas se mueven hacia la derecha. Durante la manipulación, las cuentas se mueven hacia la izquierda. Para facilitar la visualización, las dos cuentas centrales de cada hilo (la 5ª y 6ª cuenta) suelen ser de un color diferente al de las otras ocho cuentas. Del mismo modo, la cuenta izquierda del hilo de los miles (y el hilo del millón, si lo hay) puede tener un color diferente.
Como dispositivo sencillo, barato y fiable, el ábaco ruso se utilizaba en todas las tiendas y mercados de la antigua Unión Soviética, y su uso se enseñaba en la mayoría de las escuelas hasta la década de 1990. Ni siquiera la invención en 1874 de la calculadora mecánica, el aritmómetro Odhner, los había sustituido en Rusia; según Yakov Perelman, incluso en su época, se sabe que algunos empresarios que intentaban importar tales dispositivos al Imperio Ruso se daban por vencidos y se marchaban desesperados después de que se les mostrara el trabajo de un hábil operador de ábacos. Asimismo, la producción masiva de aritmómetros Felix desde 1924 no redujo significativamente su uso en la Unión Soviética. El ábaco ruso comenzó a perder popularidad sólo después de que se iniciara la producción en masa de microcalculadoras en la Unión Soviética en 1974. Hoy en día se considera un arcaísmo y se sustituye por la calculadora de mano.
El ábaco ruso fue llevado a Francia alrededor de 1820 por el matemático Jean-Victor Poncelet, que sirvió en el ejército de Napoleón y había sido prisionero de guerra en Rusia. El ábaco había caído en desuso en Europa occidental en el siglo XVI con el auge de la notación decimal y los métodos algorítmicos. Para los contemporáneos franceses de Poncelet, era algo nuevo. Poncelet lo utilizó, no para ningún fin aplicado, sino como ayuda para la enseñanza y la demostración. Los turcos y el pueblo armenio también utilizaban ábacos similares al schoty ruso. Los turcos lo llamaban coulba y los armenios choreb.