Svar 7 – 7 – 7 = 73 Detta är ”sju i kubik”

Att förstå exponenter och kvadratrotsar

Lärandemål

– Utvärdera uttryck som innehåller exponenter.

– Skriv upprepade faktorer med hjälp av exponentiell notation.

– Hitta en kvadratrot av en perfekt kvadrat.

Exponenter ger ett speciellt sätt att skriva upprepad multiplikation. Tal som skrivs på detta sätt har en särskild form, där varje del ger viktig information om talet. Att skriva tal med hjälp av exponenter kan också spara mycket utrymme. Den omvända operationen av multiplikation av ett tal med sig själv kallas att hitta kvadratroten av ett tal. Denna operation är användbar vid problem om arean av en kvadrat.

Exponentiell notation är ett speciellt sätt att skriva upprepade faktorer, till exempel 7 – 7. Exponentiell notation har två delar. Den ena delen av notationen kallas basen. Basen är det tal som multipliceras med sig själv. Den andra delen av notationen är exponenten eller potensen. Detta är det lilla tal som skrivs högt upp till höger om basen. Exponenten, eller potensen, anger hur många gånger basen ska användas som en faktor i multiplikationen. I exemplet kan 7 – 7 skrivas som 72, 7 är basen och 2 är exponenten. Exponenten 2 betyder att det finns två faktorer.

72 = 7 – 7 = 49

Du kan läsa 72 som ”sju i kvadrat”. Detta beror på att multiplicering av ett tal med sig själv kallas ”kvadrering av ett tal”. På samma sätt kallas det att höja ett tal till en potens av 3 för att ”kubisera talet”. Du kan läsa 73 som ”sju kubik”.

Du kan läsa 25 som ”två i femte potens” eller ”två i femte potens”. Du kan läsa 84 som ”åtta i fjärde potensen” eller ”åtta i fjärde potensen”. Detta format kan användas för att läsa alla tal som är skrivna i exponentiell notation. Faktum är att även om 63 oftast läses som ”sex kubik” kan det också läsas som ”sex i tredje potens” eller ”sex i tredje potens”.

Om du vill hitta värdet av ett tal som är skrivet i exponentiell form skriver du om talet som en upprepad multiplikation och utför multiplikationen. Två exempel visas nedan.

Finn värdet av 43.

A) 12

B) 64

C) 256

D) 43

Skrivning av upprepad multiplikation med exponentiell notation kan spara tid och utrymme. Tänk på exemplet 5 – 5 – 5 – 5 – 5. Vi kan använda exponentiell notation för att skriva denna upprepade multiplikation som 54. Eftersom 5 multipliceras skrivs det som basen. Eftersom basen används 4 gånger i multiplikationen är exponenten 4. Uttrycket 5 – 5 – 5 – 5 – 5 kan skrivas om i kortfattad exponentiell notation som 54 och lyder ”fem i fjärde potens” eller ”fem i 4:e potens”.

För att skriva upprepad multiplikation av samma tal i exponentiell notation skriver du först det tal som multipliceras som bas. Räkna sedan hur många gånger det talet används i multiplikationen och skriv det talet som exponent. Var noga med att räkna talen, inte multiplikationstecknen, för att bestämma exponenten.

Skriv 10 – 10 – 10 – 10 – 10 – 10 – 10 – 10 i exponentialskrivning.

A) 1 000 000

B) 60

C) 105

D) 106

Som du såg tidigare kallas 52 för ”fem i kvadrat”. ”Fem i kvadrat” innebär att man multiplicerar fem med sig själv. I matematiken kallar vi det att multiplicera ett tal med sig själv för att ”kvadrera” talet. Vi kallar resultatet av kvadreringen av ett helt tal för en kvadrat eller en perfekt kvadrat. En perfekt kvadrat är ett tal som kan skrivas som ett helt tal upphöjt till en potens av 2. Exempelvis är 9 en perfekt kvadrat. Ett perfekt kvadratiskt tal kan representeras som en kvadratisk form, som visas nedan. Vi ser att 1, 4, 9, 16, 25 och 36 är exempel på perfekta kvadrater.

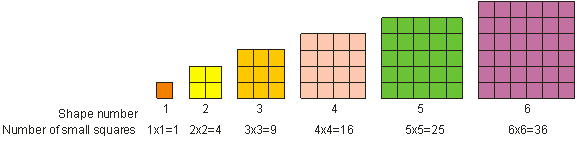
För att kvadrera ett tal multiplicerar du talet med sig själv. 3 i kvadrat = 32 = 3 – 3 = 9.

Nedan följer fler exempel på perfekta kvadrater.

Den omvända operationen för att kvadrera ett tal kallas att hitta kvadratroten av ett tal. Att hitta en kvadratrot är som att fråga: ”Vilket tal multiplicerat med sig självt ger mig det här talet?”. Kvadratroten av 25 är 5, eftersom 5 multiplicerat med sig självt är lika med 25. Kvadratrötter skrivs med en matematisk symbol, ett så kallat radikaltecken, som ser ut så här: . ”Kvadratroten av 25” skrivs .

Hitta .

A) 6

B) 18

C) 72

D) 7

Exponentiell notation är ett kortfattat sätt att skriva upprepade multiplikationer av samma tal. Ett tal som skrivs i exponentiell notation har en bas och en exponent, och var och en av dessa delar ger information för att hitta värdet av uttrycket. Basen talar om vilket tal som multipliceras upprepade gånger, och exponenten talar om hur många gånger basen används i multiplikationen. Exponenterna 2 och 3 har särskilda namn. Att höja en bas till en potens av 2 kallas att ”kvadrera” ett tal. Att höja en bas till en potens av 3 kallas att ”kubera” ett tal. Det omvända av att kvadrera ett tal är att hitta kvadratroten av ett tal. För att hitta kvadratroten av ett tal frågar du dig själv: ”Vilket tal kan jag multiplicera med sig självt för att få det här talet?”