衛星とは軌道という数学的に予測できる軌道で別の天体の周りを移動する天体です。 通信衛星は、通信、ラジオ、テレビ、インターネットアプリケーションに役立つ宇宙空間のマイクロ波リピータ局以外の何ものでもありません。 しかし、ここではこのリピータはトランスポンダとして働き、送信信号の周波数帯を受信信号と変えます。
信号が空間に送られる周波数はアップリンク周波数と呼ばれ、トランスポンダによって送られる周波数はダウンリンク周波数です。
次の図はこの概念を明確に表しています。
衛星通信 – メリット
そのような衛星通信の多くの利点があります –
-
柔軟性
-
新しい回路のインストールが容易
-
距離は簡単にカバーされているとコストは重要ではありません
-
ブロードキャスティング。 可能性
-
地球の隅々までカバー
-
ユーザーがネットワークをコントロールできる
衛星通信-デメリット
衛星通信には以下の欠点があります –
-
セグメントや打ち上げコストなど初期コストが高くなりすぎることです。
-
周波数の混雑
-
干渉と伝播
衛星通信-アプリケーション
衛星通信は以下の分野で応用されています-
-
ラジオ放送に使用されています。
-
DTHなどのテレビ放送。
-
データ転送、GPSアプリケーション、ネットサーフィンなどのためのインターネット接続の提供など、インターネットアプリケーションで。
-
音声通信用。
-
研究開発分野、多くの分野で。
-
軍事アプリケーションやナビゲーションで。
軌道上の衛星の向きは、ケプラーの法則と呼ばれる3つの法則に依存します。
ケプラーの法則
天文学者のヨハネス・ケプラー(1571-1630)は、衛星の運動に関して、3つの革命的な法則を与えましたが、その法則は次のとおりです。 衛星が主衛星(地球)のまわりを回る軌道は楕円である。 楕円は2つの焦点-F1とF2を持ち、地球はそのうちの1つである。
物体の中心から楕円軌道上の点までの距離を考える場合、中心から最も遠い楕円の点を遠地点、中心から最も短い楕円の点を近地点と呼ぶ。
ケプラーの第1法則
ケプラーの第1法則は、「すべての惑星は太陽を焦点の一つとして楕円軌道を描いて太陽の周りを公転している」とするものである。
楕円の半長軸をa、半短軸をbとする。 したがって、この系の偏心量eは-
$e = \frac{qrt{a^{2}-b^{2}}{a}$
-
Eccentricity (e) -円ではなく楕円の形の違いを定義するパラメータである。
-
半長軸 (a) – 中心に沿って二つの焦点を結んで引いた最長径で、両方の遠点(楕円の中心から最も遠い点)に接するものです。
-
準短軸(b) – 中心を通る最も短い直径で、両方の近点(楕円の中心からの最短点)に接するものです。0 < e < 1 なぜなら、eが0になると、経路は楕円形でなくなり、むしろ円形の経路に変換されるからです。
ケプラーの第2法則
ケプラーの第2法則では、「同じ時間間隔では、地球の中心に対して衛星が覆う面積は同じである。「6286>
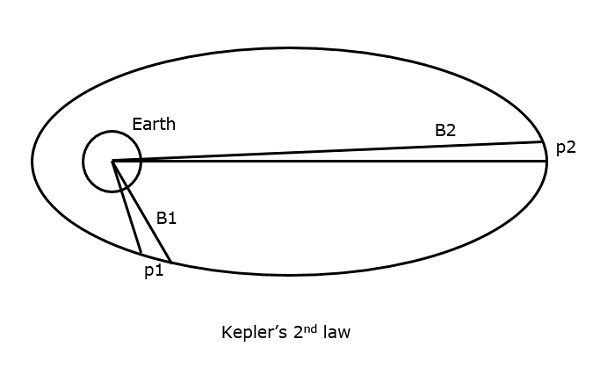
同じ時間間隔で、衛星がp1距離とp2距離を移動したとすると、両者の面積B1、B2は等しくなる。
ケプラーの第3法則
ケプラーの第3法則では、「軌道の周期時間の2乗は、2天体間の平均距離の3乗に比例する」とある。”
これを数学的に書くと
$T^{2}:\alpha:♪♪♪♪♪♪♪♪♪ となる。a^{3}$$
このことから
$T^{2} = \frac{4}pi ^{2}}{GM}a^{3}$
ここで$¥frac{4}pi ^{2}}{GM}$ は比例定数であり (ニュートン力学による)
$$T^{2} = \frac{4pi ^{2}}{mu}a^{3} $$
ここでμ=地球の地動説的重力定数である。 i.e. Μ = 3.986005 × 1014 m3/sec2
$1 = \left ( \frac{2pi}{T} \right )^{2}frac{a^{3}}{mu}$
$1 = n^{2}frac{a^{3}}{mu}୧:◜︎◜︎◜︎◜︎◝︎:a^{3} = \frac{mu}{n^{2}}$$
Where n = the mean motion of the satellite in radians per second
衛星の軌道機能は、これらのケプラーの法則を用いて計算されます。
これらに加えて、注意しなければならない重要なことがあります。 衛星が地球の周りを回るとき、地球から引かれる力、つまり重力を受けます。 また、太陽や月からも何らかの引力を受けています。 したがって、衛星には2つの力が作用しています。
-
求心力 – 軌道を描いて移動する物体を、自分自身に引き寄せようとする力を求心力と呼びます。
-
遠心力 – 軌道を描いて移動する物体を、その位置から遠ざけるように押す力を遠心力と呼びます。
そのため、衛星は軌道を維持するために、この2つの力のバランスをとる必要があります。
Earth Orbits
宇宙に打ち上げられた衛星は、科学、軍事、商業などその目的を果たすために、特定の軌道に配置されてその回転に特定の道を提供し、アクセス性を維持することが必要です。 このような衛星の地球に対する軌道を地球軌道と呼びます。 これらの軌道にある衛星は、地球軌道衛星と呼ばれます。
地球軌道の重要な種類は-
-
地球同期軌道
-
中地球軌道
-
地球低軌道
地球同期衛星
A Geo-Cynchronous Earth Orbit Satellites(地球の軌道に沿った人工衛星)です。地球同期軌道(GEO)衛星とは、高度22.5kmに位置する衛星のことです。地球上空300マイル この軌道は、横の実日数(すなわち23時間56分)と同期している。 この軌道は、傾きや離心率を持つことができます。 円形でないこともある。 この軌道は、地球の両極で傾いていることがある。 しかし、地球から観測すると静止しているように見える。
同じ地球同期軌道でも、それが円形で赤道面にある場合は、地球静止軌道と呼ばれる。 これらの衛星は、地球の赤道上空35,900km(静止軌道と同じ)に位置し、地球の方向(西から東)に対して回転し続けています。 これらの衛星は地球に対して静止しているとみなされるため、このような名前になっています。
地球静止地球軌道衛星は、天気予報、衛星テレビ、衛星ラジオ、その他の種類のグローバル通信に使用されています。 自転軸は地球の動きを示しています。
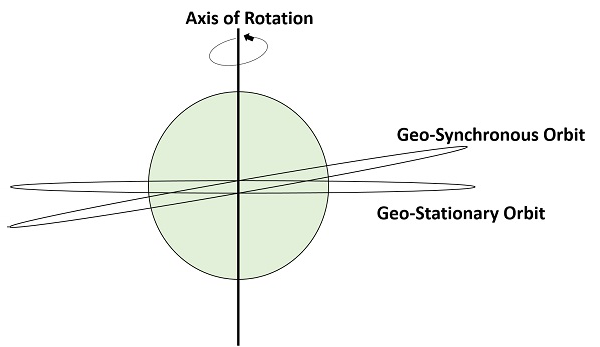
Note – すべての地球静止軌道は、地球同期軌道です。
Medium Earth Orbit Satellites
Medium Earth Orbit (MEO) satellite networks will orbit at distance of about 8000 miles from the earth’s surface. MEO衛星から送信される信号は、より短い距離を移動します。 これは、受信側での信号強度の向上につながります。 このことは、受信側でより小型で軽量の受信端末を使用できることを示しています。
衛星との間の信号の移動距離が短いので、伝送遅延も少なくなります。 伝送遅延は、信号が衛星に到達し、受信局に戻ってくるまでの時間として定義されます。 例えば、GEO衛星が往復に0.25秒を要するとすれば、MEO衛星は同じ往復に0.1秒未満で済む。 MEOは2GHz以上の周波数帯で動作する。
低軌道衛星
低軌道(LEO)衛星は、主に小型LEO、大型LEO、メガLEOの3つに分類される。 LEOは、地表から500~1000マイルの距離で周回する。
この比較的短い距離により、伝送遅延がわずか0.05秒に短縮される。 このため、高感度でかさばる受信装置の必要性がさらに低くなる。 小型LEOは800MHz(0.8GHz)帯で動作する。 メガ LEO は 2 GHz 以上の周波数帯で動作し、メガ LEO は 20~30 GHz で動作します。
メガ LEO に関連する高い周波数は、より多くの情報伝達能力を意味し、リアルタイム、低遅延ビデオ伝送スキームの能力を生み出します。
次の図は、LEO、MEO、GEOの経路を表しています。
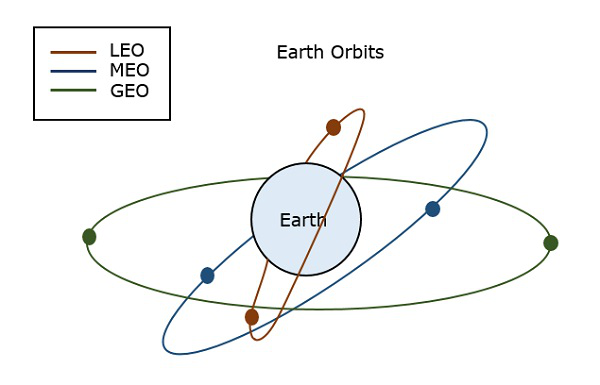 広告掲載
広告掲載 -