Intermediate Microeconomics

The Policy Question: ハイブリッド車購入税額控除-燃料消費と炭素排出を削減するための政府の最良の選択か？

米国市民と政府は、輸入された外国産石油への依存と大気中への炭素放出を懸念しています。 2005年、米国議会は、電気自動車やハイブリッド車の購入に対して消費者の税額控除を行う法律を可決しました。

この税額控除は良い政策選択のように見えますが、米国政府が徴収する歳入額を直接減少させるため、コストがかかります。 化石燃料への依存や二酸化炭素の排出を減らすために、より効果的なアプローチはあるのでしょうか？ どの政策がベストなのか、どのように判断すればよいのだろうか。 この問いに答えるには、政策立案者が何百万ドルもの連邦ドルを費やす前に、消費者がこの税制にどう反応するかをある程度正確に予測する必要がある。

この政策問題には、効用という概念を適用することが可能である。 このモジュールでは、効用と効用関数について学習する。

Exploring the Policy Question

ハイブリッド車購入補助の税額控除が大成功し、米国の道路を走るすべての車の平均燃費が2倍になったとする-この結果は明らかに現実的ではないが、その後の議論に役立つ。 米国の全自動車ドライバーの燃費はどうなると思いますか？ 政府はこれに対して、自動車の燃料消費量と炭素排出量が半分になると予想すべきでしょうか？ その理由またはそう考えない理由は何でしょうか。 効用関数を説明する。

2.2 効用関数と典型的な選好

LO 2.2.1：効用関数と典型的な選好。

2.3 効用関数と無差別曲線図の関係

LO 2.3: 効用関数から無差別曲線を導出する方法を説明する

2.4 限界効用と限界代替率を求める

LO 2.4: 典型的効用関数に対する限界効用とMRSを導く

2.5: 限界代替率から限界効用を導出する。 Policy Question

2.1 Utility Functions

LO1: Describe a utility function.

我々の選好によって、異なる消費バンドル間の比較や好ましいバンドルが選択できるようになる。 例えば、私たちの好みに基づいて、束の全セットの順位付けを決定することができる。 効用関数とは、消費財の束に数値を与えてランク付けする数学的関数であり、数値が大きいほど好ましい束であることを示す。 効用関数は、モジュール1で明らかにした選好に関する特性を持っています。 すなわち、束を順序付けることができ、完全かつ推移的であり、より少ないものよりも多いものが好まれ、関連するケースでは混合束がより良い。

効用関数が特定の束に割り当てる数値は効用として知られ、消費者が特定の束から得る満足度である。 各束の効用数は絶対的な意味では意味を持たず、満足度を測るための統一的な尺度は存在しない。 効用は、どの束が他の束より好ましいかを決定するために使用できる。

束Aからの効用が束Bからの効用より高ければ、消費者は束Bより束Aを好むと言うことと等しい。したがって効用関数は、各束に番号を割り当てて消費者の好みをランク付けする。 . 効用関数は、モジュール1で説明した無差別曲線マップを描くために使うことができます。 同じ無差別曲線上のすべての束は同じ満足を与え、したがってどれも好まれないので、各束は同じ効用を持ちます。 したがって、効用関数から同じ数値を返すすべての束を決定することで無差別曲線を描くことができる。

経済学者は効用関数は基数的ではなく序数的であると言っている。 順序型とは効用関数が束をランク付けするだけで、どれが良いかを示すだけで、他の束よりどれだけ良いかは示さないということである。 例えば、ある効用関数が、束Aは10効用、束Bは20効用を返すと示したとする。 例えば、ある友人がレースに出場し、3位になったと言ったとする。 この情報は序数的である。 あなたは、彼女が4位の選手より速く、2位の選手より遅かったことを知っています。 あなたはランナーがゴールした順番しか知らないのです。 個々のタイムは基数的なものです。 効用関数は序数であるため、多くの異なる効用関数が同じ選好を表すことができます。 これは順序が保たれている限り正しい。

例えば、財A、Bの束に対する選好を記述する効用関数U：U(A,B)を考えてみよう。 この関数に任意の正の単調変換（つまり、基本的に順序を変えない）を適用して、新しく作った関数は同じ選好を表す。 たとえば、正の定数α をかけたり、正または負の定数β を加えたりすることができる。 つまり、αU(A,B)+βは、U(A,B)と全く同じように束を並べるので、全く同じ選好を表していることになる。 効用関数の正単調変換を適用すると問題が解きやすくなることがあるので、この事実はかなり有用である。

2.2 効用関数と典型的な選好

LO2: 効用関数が表す典型的な選好に基づいて効用関数を特定する

リンゴの束Aとバナナの束Bを考える。リンゴとバナナの束に対するアイザックの選好を表す効用関数は、関数U（A，B）である。 しかし、アイザックのリンゴとバナナの束に対する特定の選好は何であろうか。 アイザックはリンゴとバナナに対して、私たちの典型的な無差別曲線を導くような、かなり標準的な選好を持っているとしよう。 彼は少ないより多い方が好きで、いろいろな種類が好きである。 このような選好を表す効用関数は次のようになる。

U(A,B) = AB

アイザックの選好でリンゴとバナナが完全補完されると、効用関数は次のようになる。

U(A,B) = MIN,

ここで MIN関数は単に二つの数字の小さい方を関数値として割り付けるだけだ。

リンゴとバナナが完全代替品である場合、効用関数は加法的で、次のようになる：

U(A,B) = A + B

Cobb-Douglas 効用関数のクラスが経済学で非常によく用いられるのは2つの理由がある。 2.非常に柔軟で、実世界のデータに簡単に適合させることができる。

Cobb-Douglas の効用関数は次のような形をしている：

U(A,B) = AαBβ

正単調変換は同じ選好を表すので、このような変換を使用して α + β = 1 と設定でき、後で見るように、消費者選択問題でいくつかの計算を簡単にするのに便利な条件であることがわかる。

効用関数を有用に変換するもう一つの方法は、関数の自然対数を取ることで、次のような新しい関数ができる：

U(A,B) = αln(A) + βln(B)

この式を導くには、単に自然対数の規則を適用する。 . ここで重要なのは、抽象度の高さを念頭に置くことである。 我々は通常、個人の嗜好を正確に表すような具体的な効用関数を作ることはできない。 おそらく、私たちの誰もが、自分自身の嗜好を一つの式で表すことはできないだろう。 しかし、一般消費者が我々の基本的な仮定に従った選好を持っている限り、我々は現実の消費データと一致する効用関数を見つけるのにかなり良い仕事をすることができます。 9015>

表2.1は、このセクションで説明した選好と効用関数をまとめたものである。1 プリファレンスの種類とそれを表す効用関数

PREFERENCES

UTTILITY FUNCTION

TYPE OF UTILITY FUNCTION

バラエティ好きか「よくばり」

U(A．B) = AB

Cobb-Douglas

Love of variety or “Well Behaved”

U(A.),B) = AαBβ

Cobb-Douglas

Love of variety or “Well behaved”

U(A,B) = αln(A) + βln(B)

Natural Log Cobb-Douglas

Perfect Complements

U(A.A),B） = MIN

Min Function

完全置換

U（A．B) = A + B

Additive

2.のようになる。3 効用関数と無差別曲線マップの関連付け

LO3: 効用関数から無差別曲線を導く方法を説明する

無差別曲線と効用関数は直接関係があります。 実際、無差別曲線はグラフで、効用関数は数学的に選好を表すので、効用関数から無差別曲線を導くことができる。

一変量関数では、y=f（x）のグラフのように従属変数を縦軸に、独立変数を横軸にプロットされる。 これに対し、2変数関数のグラフはU=U(A,B)のように3次元である。 図2.1は、U=A^frac{1}{2}B^frac{1}{2}のグラフである。 立体グラフは、AとBの消費量が増えるほど効用が増えることを理解するのに役立つ。

Figure 2.1 U=A^frac{1}{2}B^frac{1}{2}

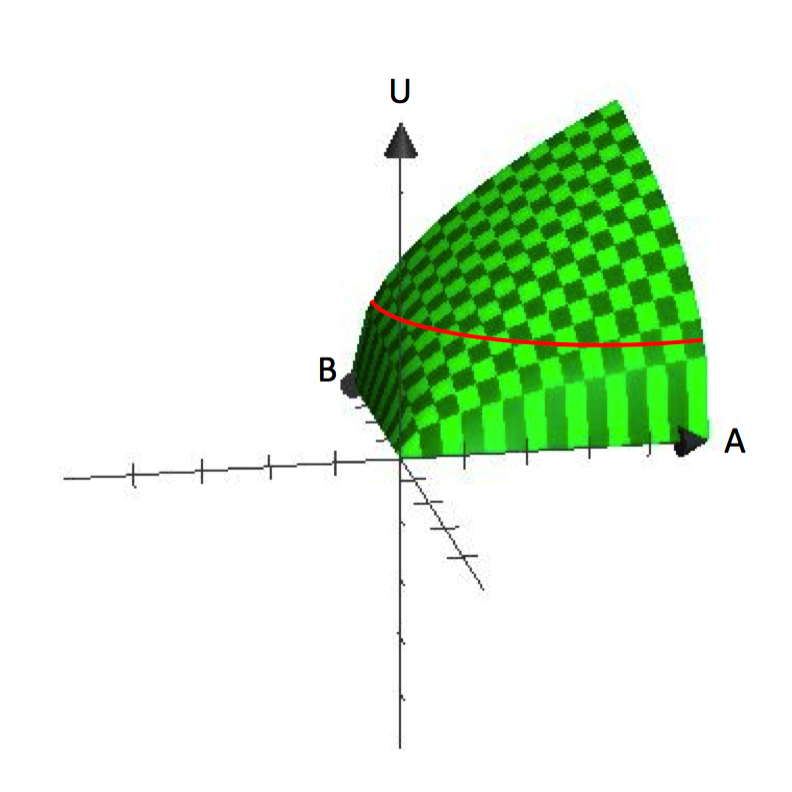
図から消費者が多様性を好むという前提が明らかである。 AとBを一定量ずつ含む各束は、表面上の点を表す。 表面の垂直方向の高さは効用のレベルを表している。 AとBの両方を増やすことで、消費者は表面上のより高い点に到達できる。

では、無差別曲線はどこから来るのだろうか。 無差別曲線とは、消費者がどれを消費するかに関して無関心なすべての束の集合体であることを思い出してください。 数学的には、効用関数に入れると、すべてのバンドルが同じ関数値を返すということと同じである。 つまり、効用にある値Ūを設定し、その値を生み出すAとBの束をすべて求めれば、無関心曲線が定義されます。 これは図2.1の三次元表面で消費者が同じ高さになる束をすべて求めることと同じであることに注意してください。

無差別曲線は平面上の標高（効用水準）を表現したものです。 地形図の等高線と同じようなものです。 3次元のグラフを2次元の空間（A,B空間）に戻すと、異なる標高や効用レベルを表す等高線・差分曲線が表示されることになる。 図2.1のグラフから、この効用関数が原点に対して「弓なりに」または「凹んだ」無差別曲線を生み出すことがすでにわかる。

つまり無差別曲線は効用関数から直接導かれ、2次元グラフで効用関数を表すのに便利な方法である。

2.4 限界効用と限界代替率を求める

LO4: 典型的効用関数に対する限界効用とMRSを求める。

限界効用とは、ある財を1単位追加消費したときに消費者が受け取る追加の効用である。 数学的には次のように表現する：

MU_{a}=Centafrac{Delta \cup }{Delta A}

または消費したAの量の変化による効用の変化（Δは項目の価値の変化）。 つまり、

MU_{a}=Cfrac{Delta \cup }{Delta A}=Cfrac{cup (A+Delta A,B)-U(A,B)}{Delta A}

なお、Aの消費の限界効用を調べるときにはBを一定とする。

微積分を使うと、限界効用は効用関数のAに関する偏微分と同じになる：

MU_{A}frac{partial U(A,B)}{partial A}

サラダとピザを食べる消費者を考えてみよう。 サラダの量は一定で、例えば夕食にサイドサラダを1つ付けるとします。 ここで、ピザの枚数を増やしてみましょう。1枚だと効用は10、2枚だと18、3枚だと24、4枚だと28になるとします。 これらの数値を、効用を縦軸に、ピザを横軸にとったグラフにプロットしてみましょう（図2.2）。 限界効用逓減のグラフと表

Pizza Slices	Utility	Marginal ユーティリティ
1	10
2	18	8
3	24	6
4	28	4

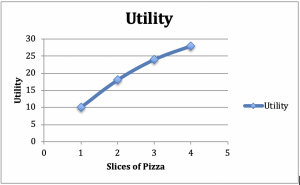
グラフの正の傾きから。 ピザを1枚追加することによって効用は増加することがわかります。 グラフの凹型から、もう一つの共通の現象を見ることができます。 ピザ1枚を追加するごとに消費者が受け取る追加効用は、消費枚数が増えるにつれて小さくなる。

ピザ1枚を追加するごとに追加効用が小さくなることを、限界効用逓減の原理という。 この原理は、混合束が好まれるような行儀の良い選好に適用される。

限界代替率（MRS）とは、消費者がある財をあきらめて、別の財をもう1単位手に入れたいと思う量です。 これは、無差別曲線の傾きと同じものです。満足度を一定に保つので、ある財と別の財を交換するときに、同じ無差別曲線上を移動するだけなのです。

先ほどの例でいえば、サラダを1つ多く食べることで効用が10増えるなら、現在ピザを4切れ消費している場合、ピザを2切れあきらめれば、28効用から18効用になる。 サラダで10効用増え、ピザを2枚諦めることで10効用減るので、全体の効用は変わらないので、同じ無差別曲線上にいることになります。 つまり、横軸の財をより多く得るために縦軸の財をあきらめることになり、その結果、正の移動に対して負の移動が生じます。 我々の場合、効用関数U=U(A,B)に対して、MRSは次のように表される：

MRS=-efficient{MU_{A}}{MU_{B}}

なお、置換すると式は簡略化できる。

MRS=-asis{MU_{A}}{MU_{B}}=-asis{MU_{Delta U}{Delta A}}{mu_{Delta U}{delta B}}=-asis{mu_{Delta B}{delta A}

Inserting the calculus it equates to:

MRS=-{partial U(A,B)}{partial A}}{{frac{partial U(A,B)}{partial B}}

2.5 Policy Question

モジュール1では、走行距離の増加とその他の消費との間の関連する消費者の決定は、おそらく消費者選択に関する標準的な仮定に適合していると判断しました。 したがって、他の財を消費するだけでなく車を運転することも好きで、それらをトレードオフとみなす消費者を表すためにCobb-Douglas効用関数を使うことは良い選択です（ガソリンに使うお金は他の消費財に使われないお金です）。 また、仮定に準拠し、かつ柔軟性があるという利点もある：

U(MD,C)=MD^{a}C^{beta }.

ここで、MD = Miles driven, C = Other consumption。

実際、関数自体は、この市場、消費者の車の走行距離の市場に対してパラメータと推定できる現実世界のデータに取ることができる。

図2.3 政策例の無関心曲線のグラフ

政策の質問を探る：

1 . この例では他の選好タイプがより適切でしょうか。

2. この政策を分析するのに使うべき選好タイプとして、完全補欠はどうあるべきでしょうか。

完全代替はどうあるべきなのでしょう。 運転する「典型的な」消費者を考えているとすると、「典型的な」効用関数を選ぶのは適切か。

4. 私たちは単なる推測なのか、それとも「行儀の良い」選好やCobb-Douglas効用関数の選択を裏付ける理論上の根拠があるのか。

SUMMARY

Review: トピックと関連する学習成果

2.1 効用関数

LO 2.1.効用関数

2.1: 効用関数を説明できる

2.2 効用関数と典型的な選好

LO 2.2。 効用関数が表す典型的な選好に基づいて効用関数を特定する

2.3 効用関数と無差別曲線図の関係

LO 2.3: 効用関数から無差別曲線を導く方法を説明する

2.4 限界効用と限界代替率の算出

LO 2.4: 典型的効用関数に対する限界効用とMRSを導き出す

2.5. Policy Question

Learn: 主要用語とグラフ

バイ変量関数

カーディナル

等高線

限界効用逓減

関数

限界代替率（MRS）

限界効用順序

一変量関数

効用

グラフ

3次元効用関数と等高線

方程式

Cobb-…ダグラス

完全な補完

完全な代替