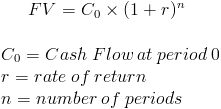
Future Value (FV) は、当初受け取ったキャッシュフローよりも後の日付の価値を計算するために金融で使われる数式である。 このように、現在の金額は将来の時点と異なる価値があるという考え方は、貨幣の時間的価値に基づくものです。
貨幣の時間価値とは、先に受け取った金額は、同じ金額を後の時間に受け取った場合よりも価値があるという考え方である。 たとえば、今日100ドルか5年後に100ドルかを提示された場合、この金額を今日受け取った方が良いという考え方です。 この金額を投資や貯蓄に回さない場合の機会費用は、将来価値の計算式で数値化される。 今日100ドルを受け取る代わりに、1年後に何ドルを受け取りたいかを判断する場合、将来価値の計算式が使われます。 ページ下部の例をご覧ください。
将来価値の計算式は、複利の効果も見ています。 毎月0.5%ずつ稼ぐのと、毎月の収益を再投資すると仮定して年間6%稼ぐのでは、同じではありません。 月が進むにつれて、次の月の収益が前の月の収益に追加でお金を稼ぐことになります。 たとえば、1つは月1で40ドルの利息を獲得した場合、次のmonthwillは、元のバランスに加え、前月から40ドルの利息を獲得します。 これは複利として知られています。
将来価値の使用
将来価値の公式は、基本的に金融のすべての分野で使用されています。 多くの状況で、将来価値の公式は他の公式の中に組み込まれています。 一例として、利子口座に定期的に預金する形の年金は、各預金の将来価値の合計となる。
Example of Future Value Formula
A individual is like to determine their ending balance after one year on a account that earns per month .5% with compounded monthly.A.P.O. (ある個人が、月利0.5%の複利計算の口座の1年後の残高を知りたいとします。 口座の元の残高は1000ドルである。 この例では、元の残高 (初期キャッシュフローまたは現在価値とも呼ばれる) は 1000 ドル、r は .005 (.5%) 、n は 12 (月) です。
これを式に当てはめると、次のようになります:
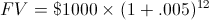
解いた後の、12 ヶ月後の残高は $1061.68 となります。 この例で得られる追加の1.68ドルは、複利計算によるものです。
別の計算式
将来価値の計算式は、次のように表すこともできます。
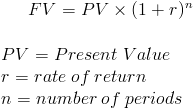
Return to Top
- 将来価値に関する式
- 現在価値
- 将来価値の係数
- 期間数を解く-
- 将来価値の係数 PV & FV
- FV – 連続複利計算