9.1 A historical example
哲学者デイヴィッド・ヒューム(1711-1776)は優れた懐疑経験主義者として記憶されています。 あるトピックについて、そのトピックに関する知識を構成するものに対して非常に厳しい基準を持っていると同時に、その厳しい基準を満たすことはできないと考える人が懐疑論者であると言えます。 経験主義とは、人間は主として経験、特に感覚的な経験を通じて知識を得るという考え方である。 ヒュームは、著書『An Inquiry Concerning Human Understanding』の中で、知識に関する原則を示し、次に図書館を掃除するように勧めています。 たとえば、神学や学校の形而上学の本を手に取ったら、「量や数に関する抽象的な推論が書かれているか」と聞いてみよう。 いいえ、事実と存在の問題に関して、実験的な推論が含まれていますか? いいえ。では、それを炎に投じてください。なぜなら、そこには詭弁と幻想しか含まれていないはずですから」
ヒュームは、知識の唯一の源泉は論理的または数学的推論(彼はこれを上記の「量または数に関する抽象的推論」と呼ぶ)か感覚経験(「事実と存在の問題に関する実験的推論」)だと考えている。 ヒュームは、どちらかの方法に基づかない主張は無価値であると主張するようになる。
ヒュームの主張を次のように再構成することができる。 tは我々が知識を持っていると主張するあるトピックであるとする。 この知識は経験や論理から得たものではないとする。 英語で書くと、次のように彼の議論を再構築することができる:
我々は、tについての我々の主張が実験的推論から、あるいは論理や数学から学んだ場合のみ、tについての知識を持っているのである。
tに関する我々の主張が実験的推論から学ばれない。
tに関する我々の主張が論理や数学から学ばれない。
我々はtに関する知識を持たない。
この「もし、もし」という表現はどういう意味か? 哲学者は、このフレーズといくつかの同義語が推論でよく使われると考えています。
P: We have knowledge about t.
Q: Our claims about t are learned from experimental reasoning.
P: We have knowledge about t.
Q: We have knowledge about t.
P: We have knowledge about t.if and only.If, only.今は説明されていないままに、次の翻訳キーで我々の提案論理と英語の混合で論を書き上げることができる。
R: tに関する我々の主張は論理や数学から学んだものである。
P if and only if (QvR)
¬Q
¬R
¬P
我々の仕事は、我々の論理言語に「もし、もし」に相当するものを追加することである。 そして、このヒュームの議論の再定式化を評価することができる。
9.2 双条件
「もし、もしも」と同義の記号を導入し、その構文と意味論を整理する前に、まず観察から始める必要がある。 P if and only if Q」のような表現は「P if Q and P only if Q」を省略した言い方であるように見える。 このことに気づけば、専門的な英語の理解で「if and only if」の意味を見極めようとする必要はないのである。 その代わり、「もし」「そして」「もしだけ」の厳密な定義を使えば、「もしだけ」の意味がわかるのである。 具体的には、「P if Q and P only if Q」は、「((Q→P)^(P→Q))」と訳すことになる。 (これが曖昧な場合は、2.2節に戻って復習してください。) さて、この式の真理値表を作ってみましょう。
| p | q | (q →p) | (p →q) | ((q→p)^(p→q))) |
| t | f | t | t | |
| t | t | f | t<9910>の場合 | f |
| f | t | f | f | |
| f | F | T | T |
これで「もし、もしも」の意味論は解決しましたね。 ここで、この表現に新しい記号を導入することができる。 二重矢印の「↔」を使うのが伝統的である。 これで「↔」の構文と意味論を表現できる。
If Φ and Ψ is sentences, then
(ΦΨ↔)is a sentence.である。 この種の文は一般に「二条件」と呼ばれる。
その意味論は次の真理値表で与えられる。
| φ | ψ | (φ↔ψ) | |
| t | t | t | |
| t | f | f | F |
| F | F | T |
二条件式の説明で喜ばしい結果の一つは、論理的同等性の統語概念を簡潔に説明できるようになったことである。 (ΦΨ↔) が定理である場合、2つの文ΦとΨは「同等」または「論理的に同等」であると言う。
9.3 代替表現
英語では、通常2条件と同じ意味を持ついくつかの表現があるようだ。 次の各文は(P↔Q).
P if and only if Q.
P just in case Q.
P is necessary and sufficient for Q.
P is equivalent to Q.
9.4 biconditionalを使った推論
biconditionalを使ってどう推論すればよいか…。 最初はほとんど指針がないように思えます。 もし私が(P↔Q)と知っていれば、PとQが同じ真理値を持っていることは分かるが、その文だけでは両方が真か両方偽かは分からない。 しかし、二条件式の意味論を利用して、二条件式を構成する一方の文の真理値も知っていれば、他方の文の真理値も導けることを観察することができる。 このことは、簡単なルールセットを示唆している。 実際には4つの規則があるが、ここでは「同値性」という一つの名前でまとめておくことにする。
(Φ↔Ψ)
Φ
_____
Ψ
(ΦΨ)
Ψ
Φ
と
(ΦΨ)
¬Φ
_____
¬Ψ
and
(φ↔Ψ)
¬Ψ
_____
¬Φ
代わりに二条件を示そうとしたらどうでしょう。 ここで、二条件(Φ↔Ψ)が((Φ→Ψ)^(Ψ→Φ))と等価であるという洞察に戻ることができます。 (Φ→Ψ)と(ΦΨ↔)の両方を証明できれば、真でなければならないことがわかる。
この規則を「bicondition」と呼ぶことができる。 これは次のような形をしている:
(Φ→Ψ)
(Φ↔Ψ)
つまり、二条件の証明を目指す場合、二つの条件導出を引き受けて、二条件規則を使うことが多い。 すなわち、二条件式の証明の多くは次のような形式である:
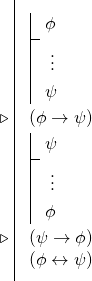
9.5 ヒュームに戻る
ここで、ヒュームの議論を証明できるかどうか確認できる。 新しい二条件記号が与えられた今、我々は3つの前提で直接証明を始めることができる。

我々はすでに、¬Qと¬Rのために(QvR)は偽だと思うことを観察している。 そこで、¬(QvR)を証明してみよう。 この文は、今ある前提を考えると、直接証明することはできません。また、条件付き証明で証明することもできません。 そこで、間接的な証明を試みよう。 我々は¬(QvR)が真であると信じているので、これを否定することを仮定して矛盾を示す。

ヒュームの議論は、少なくとも我々が再構築したように有効である。
ヒュームの議論は健全だろうか。 それが健全かどうかは、上記の第一前提に依存する(第二、第三前提は何らかのトピックtに関する抽象的なものであるから)。 具体的には、実験や論理で示すことができる場合にのみ、我々は何かについての知識を持っているという主張次第である。 ヒュームは、実験や観察、あるいは論理や数学によるものではない主張を含むテキストを信用しない、いや、燃やすべきだと主張する。 しかし、この主張を考えてみよう:我々がトピックtについての知識を持つのは、tについての主張が実験から学んだか、tについての主張が論理や数学から学んだ場合のみである<2183><3972>ヒュームはこの主張を実験によって発見したのだろうか? それとも論理学によって発見したのだろうか。 もし我々が彼のアドバイスに従ったら、ヒュームの本はどんな運命をたどるだろうか。
9.6 いくつかの例
我々がどのように二条件を使って推論できるかを説明するために、二条件を利用したいくつかの定理を証明すると便利であろう。 2つの文が第3の文と同じ真理値を持つ場合、それらは互いに同じ真理値を持つ。 これを(((P↔Q)^(R↔Q))→(P↔R))と表現する。 二条件での推論を説明するために、この定理を証明してみよう。
この定理は条件付きであるから、条件付きの導出が必要になる。 条件式の帰結は二条件式なので、(P→R)の証明と(R→P)の証明の2つの条件導出が必要になると予想される。 証明はこのようになります。 よく勉強してください。

数学者オーガスタス・ドゥ・モーガン(1806-1871)に因んで、今日では「ド・モルガンの法則」または「ド・モルガン等価」と呼ばれている原則を前に述べました。 これは、¬(PvQ)と(¬P^¬Q)が等価であること、¬(P^Q)と(¬Pv¬Q)が等価であることを認めるものである。 これらを二条件式で表現できるようになった。 以下は我々の論理の定理である:
(¬(PvQ)↔(¬P^¬Q))
(¬(P^Q)↔(¬Pv¬Q))
このうち第二定理を証明しよう。 これはおそらく今まで見た中で最も難しい証明で、入れ子になった間接証明と、関連する矛盾が何であるかを見つけるのにかなりの知恵が必要である。

9.7 定理の使用
我々の論理の各文は意味上、3種類のうちの1つである。 それは同語反復文、矛盾文、偶発文のいずれかである。 同語反復」(真でなければならない文)と「矛盾文」(偽でなければならない文)については既に定義した。 偶発文とは、トートロジーでも矛盾文でもない文のことである。 したがって、偶発文は真であるかもしれないし、偽であるかもしれない文である。
以下にそれぞれの文の例を示す。
(Pv¬P)
(P↔¬P)
P
最初のものはトートロジー、次のものは偶発的文章である。 これは真理値表で見ることができる。
| P | ¬P | (Pv¬P) | (P↔¬P) | P |
| T | F | T | F | T |
| F | T | F |
同語反復の否定は矛盾であることに注意すること。 矛盾の否定はトートロジーであり、偶発文の否定は偶発文である。
¬(Pv¬P)
¬(P↔¬P)
¬P
| P | ¬P | (Pv¬P) | ¬(Pv¬P) | (p↔p) |
| t | f | t | ||
| F | T |
少し考えれば、矛盾文や偶発文が我々の命題論理の定理であったら、かなりの惨事になることがわかるでしょう。 我々の論理は有効な論証のみを生成するように設計されている。 前提を持たない論証は、結論が真でなければならない(これも、前提を持たずに証明できる文は、どんな前提でも証明できるので、どんな前提でも真であるに違いない)。 もし、ある定理が矛盾していたら、私たちは虚偽を証明できることを知るだろう。 定理が偶発的であれば、虚偽を証明できることもある(つまり、ある条件の下では虚偽である文章を証明することができる)。 また、証明方法として間接導出を採用していることから、論証の中に矛盾や矛盾文があれば、何でも証明できることになる。
定理は論証において非常に有用である。 例えば、スミスもジョーンズもロンドンに行かないことがわかっていて、それゆえジョーンズはロンドンに行かないことを証明したいとする。 もし、ド・モルガンの定理の一つを使うことを許せば、この議論を素早く行うことができます。
P: Smith will go to London.
Q: Jones will go to London.
そして、以下の論証があります:
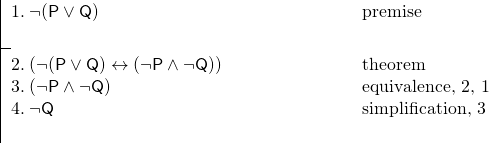
この証明は、2行目で定理を使ったので非常に簡単にできました。 まず、ある文が定理であることが分かっていれば、その定理を準証明で証明できることが分かっているので、これを許容しておくことです。 つまり、上の2行目を(¬(P v Q)↔(¬P ^ ¬Q))を証明する長いサブプルーフに置き換え、それを使うことができるのです。 しかし、(¬(P v Q)↔(¬P ^ ¬Q))が定理であることが確かならば、定理を利用するたびにこの証明を何度もする必要はないはずです。
次に認識すべき問題はもっと微妙なものです。 我々の定理のような形の文は無限にあり、それらも使えるはずである。 例えば、次のような文は、文字が違うだけで、それぞれ我々の定理の証明(¬(P v Q)↔(¬P ^ ¬Q))と同一の証明を持つことになる。
(¬(R v S) ↔(¬R ^ ¬S))
(¬(T v U) ↔(¬T ^ ¬U))
(¬(V v W) ↔(¬V ^ ¬W))
これは、できれば明白にしておきたいと思うのです。 (¬(P v Q)↔(¬P ^ ¬Q))の証明で、Pの各インスタンスをRに、Qの各インスタンスをSに置き換えれば、(¬(R v S)↔(¬R ^ ¬S))の証明になります。
しかし、ここではあまり目立たないことがあります。 以下の各々は、定理(¬(P v Q)↔(¬P ^ ¬Q))に似ていると考えることができる。
(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))
(¬(T v (Q v V))↔(¬T ^¬(Q v V))
(¬(Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^¬(R→¬ Q)))
例えば、以下のように。 (¬(P v Q)↔(¬P ^ ¬Q))の証明を、Pの各初期インスタンスを(Q↔P)に、Qの各初期インスタンスを(¬R→¬Q)に置き換えると、以下のようになります。 とすれば、定理(¬((Q↔P) v (¬R→¬Q))↔(Q↔P) ^¬(¬R→¬Q)) の証明になるのです。
この洞察は2つの方法で捉えることができる。 メタ言語の定理を記述し、それがインスタンスを持つことを許容することができる。 したがって、(¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) をメタ言語の定理とすることができ、その中で、各Φを文、各Ψを文に置き換えて、定理の特定のインスタンスを得ることができるのです。 もう一つの方法は、ある定理から置換によって他の定理を生成することを認めることである。 簡単のために、私たちはこの2番目の方法を取ります。
私たちのルールは次のようになります。 一度定理を証明すれば、いつでもそれを証明に引用することができる。 我々の正当化は、その主張が定理であることである。 我々は、定理におけるその原子文の各初期インスタンスを同じ文に置き換える場合に限り、定理における任意の原子文の他の文への置換を許可する。
例を検討する前に、いくつかの有用な定理をリストアップすることが有益である。 我々の言語には無限に多くの定理があるが、この10個はしばしば非常に有用である。 そのうちのいくつかは既に証明されています。 他のものは練習として証明することができる。
T1 (P v ¬P)
T2 (¬(P→Q) ↔ (P^¬Q))
T3 (¬(P v Q) ↔ (¬P ^ ¬Q))
T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))
T5 (¬(P ↔ Q) ↔ (P ¬Q))
T6 (¬P → (P → Q)))
T7 (P →(Q →P))
T8 ((P→Q) →(P→R))
T9 ((¬P→¬Q) →(¬P→Q) →P))
T10 ((P→Q) →(¬Q→¬P))
いくつかの例から、定理を用いる利点は明らかであろう。 上の議論を土台にして、別の議論を考えてみましょう。 スミスがロンドンに行けばベルリンに行くというわけでも、ジョーンズがロンドンに行けばベルリンに行くというわけでもないことは分かっている。 ジョーンズがベルリンに行くということがないことを証明したい。
R: Smith will go to Berlin.
S: Smith will go to Berlin.をキーに追加する。 ジョーンズはベルリンに行くだろう。
そして、次のような議論がある:
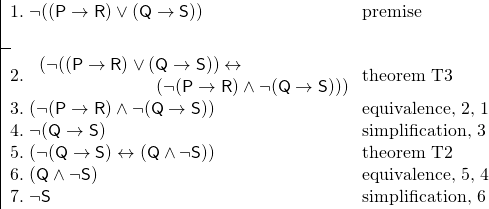
定理を使うことで、この証明は他のものよりずっと短くなった。 また、定理はしばしば証明を容易にします。定理をトートロジー(真でなければならない文)として認識するからです。
9.8 問題
- 以下の各論証が有効であることを証明せよ。 P、¬Q。 結論 ¬(P↔Q).
- 前提。 (¬PvQ), (Pv¬Q)です。 結論:(Pv)、(Pv¬Q)。 (P↔Q).
- 前提となる。 (P↔Q), (R↔S) . 結論: ((P^R)↔(Q^S)).
- 以下の各定理を証明せよ.
- T1
- T2
- T5
- T6
- T7
- T8
- T9
- ((P^Q)↔¬(¬Pv¬q))であることを確認する。
- ((p→q)↔¬(p^¬q))
- 普通の口語的な英語で、少なくとも2つの前提、少なくともそのうちの1つは二条件である、あなた自身の有効な議論を書きなさい。 あなたの議論は単なる段落であるべきです(文の順序付きリストや形式論理のようなものではありません)。 それを命題論理に変換し、それが有効であることを証明せよ。
- 普通の口語的な英語で、少なくとも2つの前提条件と、2つの条件である結論で、あなた自身の有効な議論を書きなさい。 あなたの議論は単なる段落であるべきです(文の順序付きリストや、論理のように形式的に見える他のものではありません)。 1596>
Selby-Bigge and Nidditch (1995 )のヒュームのEnquiry Concerning Human Understanding, p.161 より。