中性子の崩壊
|
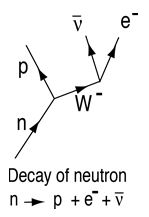
自由中性子は半減期約10.3分で崩壊するが、原子核に結合すれば安定である。 この崩壊は電子と電子反ニュートリノの放出を伴うベータ崩壊の一例である。 中性子の崩壊には、右のファインマン図に示すような弱い相互作用が関与している。 |
 |
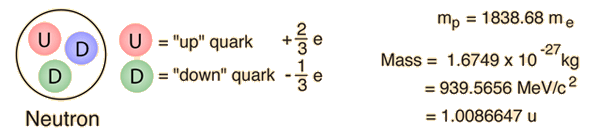
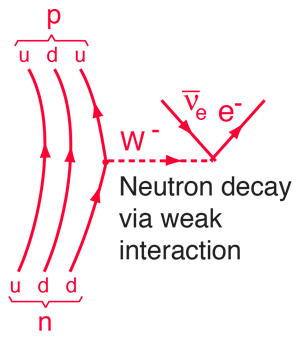 |
より詳しい崩壊の図では,中性子のダウンクォークの1つをアップクォークに変換するものとして同定しています。 これはベータ崩壊を含む多くの原子核過程に関与する一種のクォーク変換の例である。 |
中性子の崩壊は、ニュートリノの発見につながった観測の良い例です。 崩壊のエネルギー論的な分析は、このプロセスの初期の研究者が直面したジレンマを説明するために使用することができる。
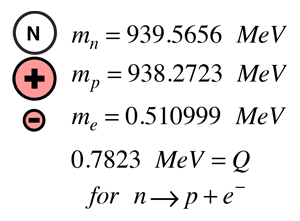 |
結合エネルギーの概念を使って、粒子の質量をその静止質量エネルギーで表し、中性子崩壊からのエネルギー収量を粒子質量から計算することができます。 エネルギー収量は伝統的に記号Qで表される。崩壊ではエネルギーと運動量が保存されなければならないので、軽い電子が運動エネルギーの大部分を持ち去ることが示される。 この大きさの運動エネルギーでは、相対論的な運動エネルギー表現を使わなければならない。 |
とりあえず、崩壊の生成物は陽子と電子だけだと仮定します(間違っています)。 この場合、エネルギー収量Qは陽子と電子で分けられます。 電子は運動エネルギーのほとんどを得るので相対論的ですが、陽子は非相対論的です。 するとエネルギーバランスは
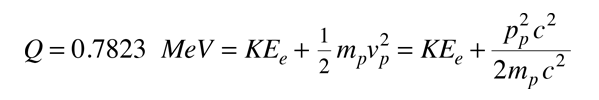
中性子の静止枠で見ると。 運動量保存は
そしてpcelectronは電子の運動エネルギー
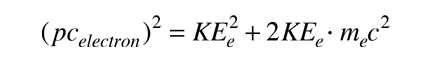 |
表示 |
すると、エネルギー収支は
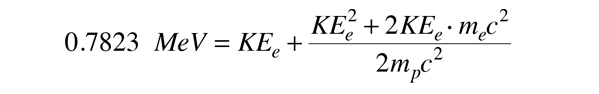
このQの値に数値を代入すると、次のようになる。 の項が無視できるので、電子の必要運動エネルギーが計算できることがわかります。 この2粒子崩壊の方式で必要な電子の運動エネルギーは
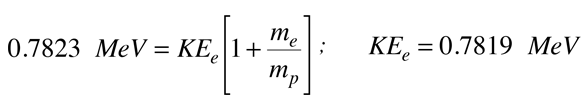
同様に、この2粒子崩壊の電子の運動量は

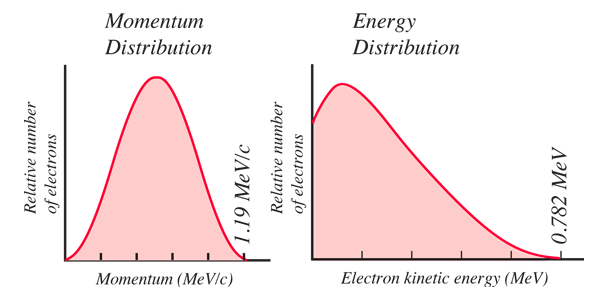
中性子崩壊で生成された電子がエネルギーと運動量の連続した分布を持っているということは、電子と陽子とともに別の粒子が放出されたことを明確に示しています。 それは中性粒子でなければならず、ある崩壊では崩壊のエネルギーと運動量のほとんどすべてを担っていた。 電子の運動エネルギーが最大になったとき、それが崩壊に利用できるすべてのエネルギーQを占めていたという事実を除けば、これはそれほど驚異的なことではありませんでした。 つまり、もう一方の放出粒子の質量エネルギーを説明するためのエネルギーは残されていなかったのだ。 初期の実験者たちは,崩壊のほぼすべてのエネルギーと運動量を運ぶことができるが,電荷もなく明らかに質量もない粒子というジレンマに直面した!
この謎の粒子はニュートリノと呼ばれたが,コーワンとライネスによってニュートリノの明確な実験観測が行われるまで25年かかりました。 現在の中性子の崩壊の理解は
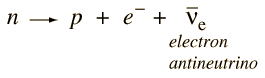
この崩壊は粒子の崩壊を支配する保存則のいくつかを例示しています。 生成物の中の陽子はバリオン数の保存則を満たすが、電子が伴わずに出現するとレプトン数の保存則に違反することになる。 レプトン数保存則を満たす崩壊をさせるためには、3番目の粒子は電子の反ニュートリノでなければならない。 電子はレプトン数1、反ニュートリノはレプトン数-1である。
ニュートリノの実験的検出
重陽子における中性子の安定性