解答 7 – 7 – 7 = 73 これは「7の3乗」と読みます。

指数と平方根の理解

学習目標

– 指数を含む式を評価すること。

– 指数表記を使って繰り返される因数を書ける。

– 完全平方根の平方根を求められる。

指数は繰り返しの乗法を書く特別な方法である。 この方法で書かれた数値は特定の形式を持ち、それぞれの部分が数値に関する重要な情報を提供します。 指数を使って数字を書くと、スペースもかなり節約できる。 掛け算の逆演算は、平方根の求め方と呼ばれます。 この操作は、正方形の面積を求める問題に役立ちます。

Exponential notation is a special way of writing repeated factors, like 7 – 7.など。 指数表記には2つの部分があります。 1つは基底と呼ばれる部分です。 ベースは掛け合わされる数そのものです。 もう一つは指数、またはべき乗です。 これは、基数の右側に高く書かれた小さな数字です。 指数、または累乗は、乗算の際に基数を何回係数として使用するかを示します。 この例では、7-7は72と書き、7が底、2が指数となる。 指数2は因数が2つあることを意味します。

72 = 7 – 7 = 49

72は “7の2乗 “と読むことができますね。 これは、数字に掛け算をすることを “数字の2乗” と呼ぶからです。 同様に、数を3の累乗にすることを “数の3乗” と言います。 73を “7の3乗 “と読むことができます。

25を “2の5乗”、または “2の5乗 “と読むことができます。 84は “8の4乗 “または “4の8乗 “と読むことができます。 この形式は、指数表記で書かれたどんな数字でも読むことができる。 実際、63は「6の3乗」と読むのが一般的ですが、「6の3乗」「6の3乗」と読むこともできます。

指数表記で書かれた数値の値を求めるには、その数値を乗法の繰り返しとして書き換え、乗法を実行すればいいのです。 以下に2つの例を示します。

43の値を求めよ。

A) 12

B) 64

C) 256

D) 43

指数表記で繰り返し掛け算を表記すると時間や場所の節約になります。 5 – 5 – 5 – 5 の例題を考えてみましょう。 この繰り返しの掛け算を指数表記で書くと、54と書けます。 5が掛け算されているので、5を底として書きます。 5 – 5 – 5 – 5という式は、指数表記で54と書き直すと、「5の4乗」または「4の5乗」となります。 次に、その数字が掛け算に何回使われたかを数え、その数字を指数として書きます。 指数を決めるときは、掛け算の符号ではなく、必ず数字を数えること。

a) 1,000,000

b) 60

c) 105

D) 106

先に見たように、52は “5 squared” と呼ばれていますね。 “5の2乗 “とは、5を掛け合わせるという意味です。 数学では、数を掛けることを「二乗する」と言います。 整数を二乗した結果を、正方形または完全平方と呼びます。 完全平方とは、2の累乗の整数として書くことができるすべての数のことです。 完全平方数は、以下のように正方形の形で表すことができます。 1、4、9、16、25、36が完全平方数の例であることがわかる。

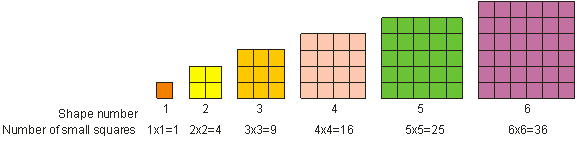
ある数を平方するには、その数に自分自身をかけることである。 3の2乗＝32＝3-3＝9.

以下、完全な2乗の例をいくつか挙げてみましょう。

数の二乗の逆の操作を、数の平方根を求めるといいます。 平方根を求めるのは、”どのような数を掛けるとこの数になるのか “を問うようなものです。 25の平方根は5であり、5を掛けると25になるからである。 平方根は、ラジカル記号と呼ばれる、次のような数学記号で表記されます。 . 25の平方根」はと書きます。

を検索してください。

a) 6

b) 18

c) 72

D) 7

指数表記は同じ数を繰り返し掛ける場合の略記法である。 指数表記で書かれた数には基数と指数があり、これらの部分はそれぞれ式の値を求めるための情報を提供します。 基数はどのような数を繰り返し掛けているかを示し、指数はその基数が掛け算に何回使われるかを示す。 指数2と3には特別な名前がついています。 底辺を2の累乗にすることを「2乗」といいます。 底辺が3の累乗になることを「3乗」といいます。 数の2乗の逆は、数の平方根を求めることである。 数の平方根を求めるには、「この数を得るために、どのような数を掛け合わせることができるか」と自問します

。