経済学におけるゲーム理論の例

ゲーム研究は、一方のプレイヤーの決定が他方のプレイヤーの行動に依存する戦略的相互作用の研究である。

Examples of Game Theory

1. Both players have a dominant strategy.

A DOMINANT strategy occurs when there is an optimal choice of strategy for each player no matter what the other does.The DOMINANT strategyは、相手が何をしても各プレイヤーにとって最適な戦略の選択が存在する場合である。

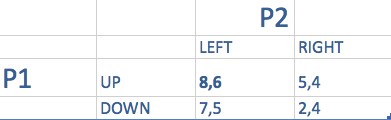
• P2が左を選べばP1はUP
• P2が右を選べばP1はUP
• したがってUPはP1

P1は何をしても必ず右に選ぶ

ユニーク均衡は（UP、左）である。 これは両者にとって最良である

1. 1人のプレイヤーが支配的戦略

PIGLET

Push lever wait for swill
Push lever 8,-2 1,7
PIG
Wait for swill 10.PIGが支配的戦略である PIGLETは、1人のプレイヤーにとって支配的戦略である
。-2 0,0

1. ブタは常に待つ
2. ブタは押すしかない

ナッシュ均衡

支配戦略を持たないゲームも多く存在する。

定義。

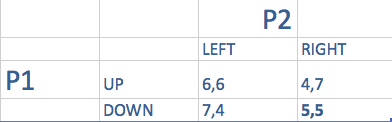
この場合、P1が下を選べば、P2は右を選ぶ

P1が上を選べば、P2も右を選ぶ。 しかし、P2が右を選ぶと、P1は下を選びたくなる。

左上が最適パレート結果であるにもかかわらず、ナッシュ均衡は右下、(5,5)になる。

談合とゲーム理論

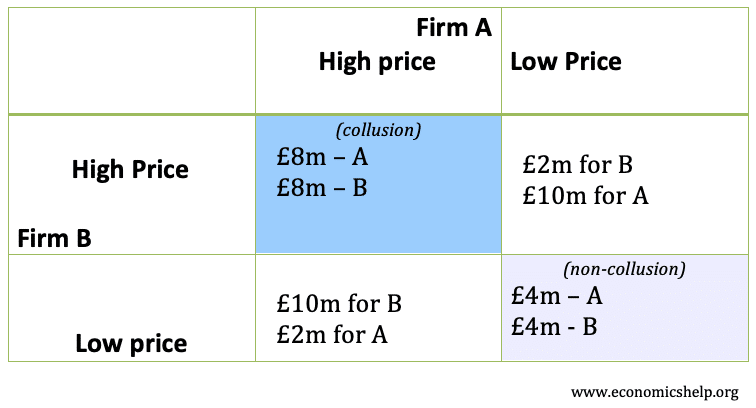
• 企業が競争し安い価格を設定していると、両者は4mポンド儲かることになる。
• 談合して高い価格を設定した場合、両者の利益は倍増し、8mポンドになる。
• しかし、談合中に企業Aが談合価格を下回り、低い価格を設定した場合、より多く売ることができる。 この場合、企業Aは両者の長所を享受する。 B社が高い価格を設定しているので価格は高いが、A社もライバルを下回っているので大量に売れるのである。 この場合、企業Aは1000万ポンド、企業Bは200万ポンドしか儲からない。
• したがって、企業Bが価格を高く維持する可能性は低く、市場はどちらも低価格を設定している状態に逆戻りである。

企業にとって最適な結果は談合（高値、高価格）

Repeated Games and Game Theory

ゲームが繰り返されれば、不正をした人を罰する可能性があり、これはパレート最適アプローチに固執するインセンティブになる

しかし、ゲームが有限回繰り返されると不正を行うインセンティブが生じることになる。 もしゲームを10回行うなら、プレイヤーは10回目で亡命してしまうので、なぜ協力するのか。 だから、したがって、9ラウンドで亡命したほうがよいので、8ラウンドも同様だ

それが無限に繰り返されるなら、それは違うだろう。 その場合、最適な戦略は、tit for tatをプレイすることです。 あるラウンドでプレイヤーが不良になったら、次のラウンドで報復するのです。 つまり、相手がすることは何でもする、これがカルテルを実施するインセンティブになるのです」

ゲーム理論。 参入抑止ゲーム

新しい企業が市場に参入した場合、ペイオフは現存の企業が戦うか受け入れるかに依存します。 戦えば両者とも0、戦わなければ現有者が1、参入者が2。 したがって、均衡は新規企業が参入し、現職が受け入れることである。

しかし、現職が戦うという信頼できる脅威を与えることができれば、彼は参入者を説得して退場させることができるかもしれない。 そのためには、価格競争においてより大きな見返りが得られるような余剰生産能力に投資すればよい。 そうすれば、参入を阻止することができます。

ゲーム理論とねじれ需要曲線

ゲーム理論は価格戦略に使用できる。

寡占状態では、企業は値下げ、値上げ、据え置きのいずれかを決定することができる。 これは、

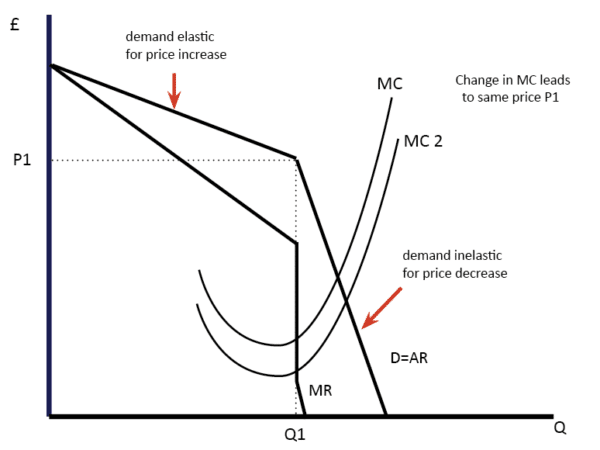
1. 企業が価格を上げると、他の企業は上げない-したがって需要は大幅に減少する。 (需要は弾力的である）
2. 企業が価格を下げれば、あなたは市場シェアの増加を得るだろう。 他の企業はこれを許さない。 したがって、彼らも値下げをする。 基本的に全員が損をする価格競争を引き起こす。

したがって、寡占状態において、企業の意思決定の重要な特徴は相互依存の影響である。 344>

Related

• ゲーム理論 – プレイステーションの値下げ

。