標準偏差は、データセット内のばらつきの平均的な量です。
高い標準偏差は、値が一般的に平均から遠いことを意味し、低い標準偏差は、値が平均の近くに集まっていることを示します。
標準偏差は何を教えてくれますか。 ほとんどの値は中心領域に集まり、中心から離れるにつれて値は先細りになります。 標準偏差は、データが平均して分布の中心からどの程度広がっているかを示します。
身長、標準化テストのスコア、仕事の満足度など、多くの科学的変数が正規分布に従います。 異なるサンプルの標準偏差がある場合、統計的検定を使ってそれらの分布を比較し、それらが由来する大きな集団についての推論を行うことができます。
平均（M）評価は、各グループで同じです – それは、曲線がそのピークにあるときにX軸上の値です。 しかし、その標準偏差(SD)は互いに異なっている。
標準偏差は分布の分散を反映している。 標準偏差が最も小さい曲線は、ピークが高く、広がりが小さく、標準偏差が最も大きい曲線は、より平坦で広がっています。
経験則
標準偏差と平均を一緒に使うと、正規分布に従っているなら分布内のほとんどの値がどこに位置するかを知ることができます。
経験則、または 68-95-99.7 の法則は、値がどこにあるかを教えてくれます：
- スコアの約 68% は平均の 2 標準偏差以内、
- スコアの約 95% は平均の 4 標準偏差以内、
- 約 99.7%が平均値から6標準偏差以内にある。
経験則に従うと、
- 得点の約68%は40から60の間にある。
- 得点の約95%は30から70の間である。
- スコアの約 99.7% は 20 から 80 の間です。
経験則は、データの概要を把握し、このパターンに従わない外れ値や極端な値をチェックするのに、手早くできる手段です。
正規分布でない場合、標準偏差はばらつきの指標としては信頼性が低く、範囲や四分位範囲などの他の指標と組み合わせて使用する必要があります。
母集団と標本の標準偏差公式
標準偏差を計算するには、母集団全体からのデータかサンプルかによって異なる公式が使用されます。
母集団標準偏差
興味のある母集団のすべてのメンバーからデータを収集した場合、母集団標準偏差の正確な値を得ることができます。
母標準偏差の公式は次のようになります。
| 式 | 説明 |
|---|---|
 |
|
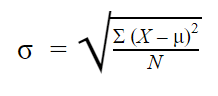サンプル標準偏差
サンプルからデータを収集するとき、サンプル標準偏差は母標準偏差についての推定または推論を行うために使用されます。
標本標準偏差の式は次のようになります。
| 式 | 説明 |
|---|---|
 |
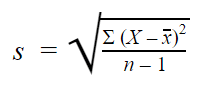s = 標本標準偏差（以下略） ＜標本標準偏差（以下略 |
サンプルでは、n を使うと常に変動を過小評価する偏った推定値になるから式では n – 1 を使うんだよ。 標本の標準偏差は母集団の実際の標準偏差よりも低くなる傾向があります。
標本nをn – 1に減らすと標準偏差が人為的に大きくなり、変動性を保守的に見積もることができるようになります。
これは不偏の推定値ではありませんが、標準偏差の推定値としてはあまり偏っていません。サンプルの変動を過小評価するよりも、過大評価する方が良いのです。
標準偏差の計算手順
標準偏差は通常、統計解析に使用するどのソフトウェアでも自動的に計算されます。 しかし、式の仕組みをよりよく理解するために、手で計算することもできます。
手で標準偏差を求めるには、主に6つの手順があります。 6つのスコアからなる小さなデータセットを使って、その手順を説明します。
| データセット | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
ステップ1: 平均を求める
平均を求めるには、すべての得点を合計し、それを得点の数で割ります。
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
Step 2: それぞれの得点の平均からの偏差値
平均値をそれぞれの得点から引き、平均からの偏差値を出します。
x̅=50なので、ここでは各点数から50を引きます。
| 得点 | 平均からの偏差 |
|---|---|
| 46 | 46 – 50 = -となる。4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
手順3.を実行する。 平均からの偏差をそれぞれ二乗する
平均からの偏差をそれぞれ乗算する。 この結果、正の数になる。
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -となります。18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
ステップ4.このような場合、どのようにすればよいのでしょうか。 平方和を求める
偏差の2乗をすべて足し算する。
16 + 361 + 324 + 100 + 4 + 81 = 886
Step 5: Find the variance
square sumをn – 1 (for a sample) or N (for a population)で割ると、これが分散となる。
サンプルサイズが6なので、n – 1を使い、n = 6とします。
886 ÷ (6 – 1) = 886 ÷ 5 = 177となります。2
ステップ6：分散の平方根を求める
標準偏差を求めるには、分散の平方根をとります。
√177.2 = 13.31
SD=13と学習することから、13.31であることから、各スコアは平均で13.31ポイント平均から外れていると言えます。
Why is standard deviation a useful measure of variability?
変動性を計算するもっと簡単な方法もありますが、標準偏差の式は均等に広がったサンプルよりも不均等に広がったサンプルを重く見ています。 より高い標準偏差は、分布がより広がっているだけでなく、より不均等に広がっていることを伝えます。
これは、平均絶対偏差（MAD）などの単純な測定値よりも、データのばらつきについてより良い考えを与えることを意味します。 まず、平均からの各偏差を正の数に変換して絶対値で表します（例えば、-3 は 3 になります）。
標準偏差と違って、MADは二乗や平方根を計算する必要がありません。
中心傾向は同じだが、ばらつきの大きさが異なる2つのサンプルを使ってみましょう。 サンプルBはサンプルAより変動が大きい。
| 値 | 平均 | 標準偏差 | ||
|---|---|---|---|---|
| サンプルA | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| サンプルB | 51, 21, 79, 49 | 50 | 15 | 23.7 |
平均値からの偏差が同じサンプルでは、MADは広がり具合を区別することができない。 標準偏差の方がより正確です。平均からの偏差の変動が大きいサンプルほど高くなります。
平均からの差を二乗することで、標準偏差はより正確に不均等な分散を反映します。
ただし、これは標準偏差を外れ値に対して敏感にします。
標準偏差に関するよくある質問
- 範囲：最高値と最低値の差
- 四分位範囲：最高値と最低値の差
- 四分位範囲：最高値と最低値の差
- 分散性：最も一般的に次の記述統計で測定します。 標準偏差：平均からの平均距離
- 分散：平均からの二乗距離の平均
標準偏差とは、データセットにおけるばらつきの平均値です。
正規分布では、標準偏差が高いと、値が一般的に平均から遠く、低いと、値が平均の近くに集まっていることを意味します。
正規分布では、データは対称的に分布し、傾きはありません。
中心傾向の指標（平均、最頻値、中央値）は、正規分布ではまったく同じです。
- 約 68% の値が平均の 1 標準偏差以内である。
- 約 95% の値が平均の 2 標準偏差以内である。7%の値が平均の3標準偏差以内である。
経験則は、データの概要を把握し、このパターンに従わない外れ値や極値がないかをチェックする手軽な方法です。
分散は平均からの偏差の二乗の平均値で、標準偏差はこの数値の平方根です。
- 標準偏差は元の値と同じ単位（分やメートルなど）で表されます。
- 分散はもっと大きな単位（メートルの2乗など）で表されます。
分散の単位は直感的に理解しにくいですが、分散は統計検定で重要な役割を担います。