このレッスンでは、次の問題を解くための簡単な方法を紹介します:二等辺三角形の面積を求める方法です。
これまで証明した性質を、次の幾何の問題で実践してみましょう。
問題
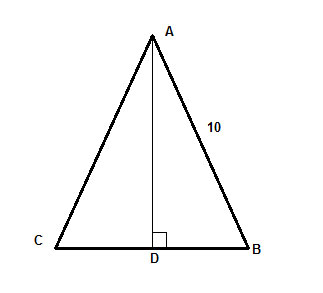
脚の長さが10の二等辺三角形ΔABCにおいて、底面までの高さは底面の3分の2に等しい。
Strategy
この問題を解くために、やるべきことから逆算します。
我々は、(底辺×高さ)/2の式で与えられることが分かっている三角形の面積を求める必要があるのですが、問題は、底辺長さも高さも分からないということです。 しかし、両者の関係は与えられているので、それがヒントになります。 底辺の長さBCをxとします。
そして、高さADは問題で与えられたように2x/3とわかります。
したがって、求めている答えは、(底辺×高さ)/2、つまりx×2x/3を2で割ったものです。
しかし、どうやってxを求めるのでしょうか。 問題で与えられたものでまだ使っていないものが二つあります。
ここで、二等辺三角形の性質を復習しておきましょう。 すぐに思いつくのは、これまで示したように、二等辺三角形では、底辺までの高さが底辺を二等分するので、CD=DB=x/2であることです。
最後に、ADは高さですから、角度∠ADCは直角であり、直角三角形ΔADCができ、その斜辺は分かっているので(10)、ピタゴラスの定理を使って足を求め、c2 =a2+b2,
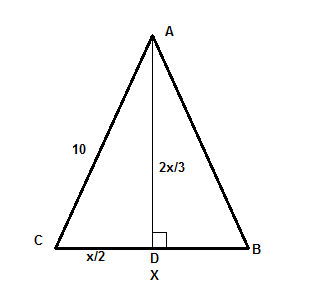
ここでc=10 ,a=x/2,b=2x/3 …とすることができるのです。 あとはxを代数的に解くだけである。
証明。 二等辺三角形の面積
(1) ΔADCが直角三角形であること //与えられる。 ADは底面の高さ
(2) AC2 =CD2 + AD2 //ピタゴラスの定理
(3) AC= 10 //与えられる
(4) CB = x
(5) CD = x/2 //2等辺三角形の底から底までの高さは底面を2等分
(6) AD = 1 //ピタゴラスの定理(9162>
) 2x/3 //与えられた
(7) 102 = (x/2)2 + (2x/3)2 //(2) に代入
(8) 100 = x2/4+4×2/9 //簡易
(9) 100*36 = 9×2 +16×2 //両側に36をかけて
(10) 100*36 = 25×2 / /同様の項を集めて
とする