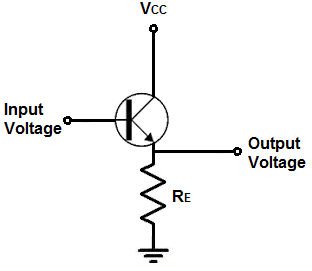
このプロジェクトでは、トランジスタを使ったバッファの作り方を紹介します。
バッファは、入力された電圧と同じ電圧を出力するデバイスで、最大の電圧転送を可能にしたり、電源から低い電流負荷を引き起こすなど、無数の用途に使用することができます。
この回路はICバッファのような集積回路を使用していません。
単純な部品しか使っていない。
使用するトランジスタはバイポーラ接合型トランジスタで、NPNタイプです。
トランジスタの回路はエミッタフォロワ(コモンコレクタ回路という別名がある)構成にする。
エミッタフォロワ回路とは、エミッタの電圧が入力電圧に追従するトランジスタ回路である。 いわば入力電圧の鏡像である。 したがって、出力の電圧は入力の電圧と同じになる。
出力電圧は入力電圧の鏡像であり、入力インピーダンスが大きく、出力インピーダンスが小さいので、エミッタフォロワはバッファとして機能する。
したがって、バッファが必要な電圧ラインはこの回路の入力に接続し、電源が必要な負荷はこの回路の出力に接続することができる。
これは、利用可能なバッファ・チップやバッファに変換できるロジック・チップを持っていない場合に最適です。
この回路では、具体的には、入力インピーダンスが 50KΩ 以上、出力インピーダンスが約 5Ωになります。 これは、バッファリングが必要な電圧に対して、かなり良いバッファ効果を生み出します。
バッファとして機能するこのタイプのトランジスタ回路を構築します。
エミッタ・フォロワ回路を正しく設計するには、トランジスタのコレクタに供給する直流電圧、トランジスタに流したい電流、入力する交流信号の周波数遮断など、いくつかの要因を考慮する必要があります。
これらの概念については、以下で詳しく説明します。 この回路では、どのように構成するか、抵抗とコンデンサの値をどのように選ぶか、これをトランジスタ・バイアスと呼びますが、その方法を紹介します。
必要な部品
- 2N3904 NPNトランジスタ
- 1KΩ 抵抗
- 1.2KΩ抵抗
- 1.1KΩ抵抗
- 500Ω 抵抗
- 16μF 電解コンデンサ
選択するトランジスタは、本当にBJT NPNトランジスタでよいのでしょうか。 この回路では、2N3904トランジスタを選択します。
実際に計算する部品の値の多くは、正確な値を見つけることができません。 例えば、以下では、抵抗の1つを565Ωと計算しています。 この抵抗は存在しません。 そこで、近似的に計算します。 500Ωの抵抗器を見つけることは可能ですし、見つからなくても1KΩの抵抗器を2個並べれば、500Ωの等価抵抗が得られます。
1.1KΩの抵抗も見つけることはできないでしょう。 そこで、1KΩに近似するか、100Ωの抵抗に1KΩの抵抗を直列に入れることになります。 基本的な用途では、これは必要ありません。 1.1KΩの代わりに1KΩの抵抗を接続するだけでよいのです。 同様の結果が得られます。
コンデンサーの値も同じ近似値を使用する必要があります。 計算されたコンデンサ値にできるだけ近い値を探し、それを使用します。
トランジスタバッファ回路
NPNBJTトランジスタ1個と抵抗、コンデンサで作るバッファ回路は下図のようになります。 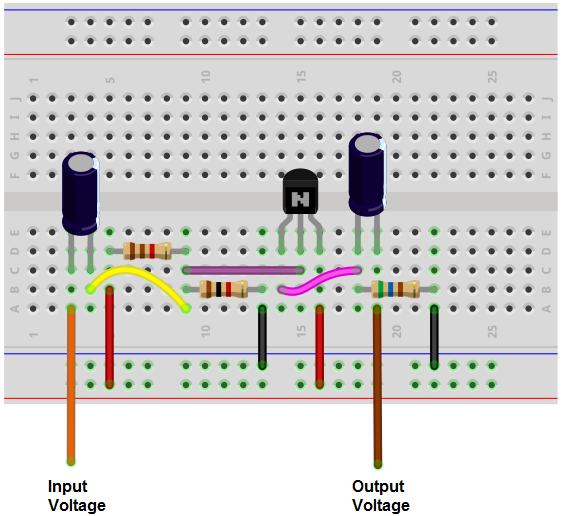
つまり、上の回路はバッファとして機能するわけです。 バッファリングしたいラインを入力に接続し、電源を入れたい負荷を回路の出力に接続します。
次に、この回路にさまざまな部品が必要な理由と、その値の選び方について詳しく説明します。
そこでまず、この回路にどれだけの電圧を供給するのかを決めます。 これはトランジスタのコレクタにかかる電圧、VCCです。 ベース電圧のVBから、トランジスタがコレクターで処理できる最大値まで、どのような値でも選択できます。 多くのトランジスタでは、40〜60Vが一般的です。 この回路では、VCCに12という妥当な電圧値を選びます。つまり、これが最初の検討事項です。
次に、VCCがわかったので、回路のベース電圧をバイアスします。これは、トランジスタのベースにかかる電圧を選択することを意味します。 これに答えるには、全体像を把握する必要があります。 トランジスタの出力に存在し得るAC電圧の量は、回路が持つDC電圧範囲に依存します。 一方、トランジスタは最大12V(VCC)までスイングすることができます。 もう一方の端では、トランジスタは約0.7Vのグランド近くまでスイングダウンすることができます。 トランジスタがグランドまでスイングできないのは、ダイオードのスイッチが入らないとトランジスタがオンにならないからで、このときの電圧は内部ダイオードのバリア電圧である約0.7Vです。 したがって、0.7Vは回路の床であり、グランドでも0Vでもない。 したがって、12Vの電源と0.7Vのグランドがあれば、トランジスタは0.7Vから12Vまで振れることになる。 なぜ、ベースに供給する電圧が重要かというと、回路に入る電圧は0.7Vが床で、12Vが天井になるからです。 したがって、ベース電圧はこの間になるようにバイアスをかけたい。 これにより、信号のピーク・トゥ・ピーク・エクスカージョンが最大となり、クリップせずに動作させるための余地が生まれます。 ベース電圧のバイアスが正しくなかったり、中間値から大きく外れていると、トランジスタは大きなクリッピングを起こし、出力が低下することがあります。 天井が12V、床が0.7Vの場合、中間値は(12 – 0.7V)/2 +0.7V= 6.35Vとなります。 ベースの値が出力より0.7V高いので、ダイオードの電圧降下を考慮しなければならない。 ベース電圧を天井と床のちょうど真ん中にバイアスすることで、最大ピーク・ツー・ピーク・エクスカーションと呼ばれる交流信号の振れ幅を最大にすることができるのです。 交流信号を扱うトランジスタ回路にバイアスをかける場合、クリップせずに出力に現れる交流信号がDCバイアスと同等になります。 交流信号は直流電圧のバイアスが許す範囲内でしか振れません。 電源が20Vでフロアーが0.7Vの場合,トランジスタは20Vのピーク値から0.7Vのフロアーまで振れることになります。 この電圧の中点にトランジスタを置くと、交流信号が天井から床まで最大に振れるようになる。 DC値が低すぎると、信号が波形の底で早くクリップしてしまいます。 この点を踏まえ、ベースの電圧は電源電圧である12Vとフロアを示す0.7Vの中間になるようにします。 つまり、VB=0.7V+(12V-0.7V)/2で、6.35Vとなるわけです。 つまり、この電圧を得るためには、この電圧がベースに現れるような抵抗器を選ばなければならない。 ベースの電圧は、2つの抵抗でバイアスされます。 抵抗は分圧器を形成し、電源電圧を分割します。 正しい値の抵抗を選択することで、電源電圧を電源電圧以下の任意の電圧に分割することができます。 ベース電圧、VB= VCC * (R2/R1+R2)です。 この式を解くには、一方の抵抗の値を選び、その抵抗の値に基づいて、もう一方の抵抗の値をこの式に基づいて計算する。 つまり、R2の抵抗は1KΩという値が選ばれ、もう一方の抵抗の基準点となる。 これらの値を式に代入すると、VB= VCC * (R2/R1+R2)= 6.35V (12V) (1KΩ)となります。 /(R1+1KΩ)となる。 計算すると、R1=1.1KΩという値になります。 つまり、ベース電圧6.35Vを得るためには、抵抗の値は、R1=1.1KΩ、R2=1KΩとなります。
次に、RE抵抗の値を決めます。 この値は、トランジスタが過熱して壊れないようにするために必要な値です。 抵抗の選び方は、トランジスタに流したい電流値IEと、トランジスタに流しても安全な電流値から決めます。 そこで、トランジスタを焼いても安全な電流を流すことができる範囲を選びます。 安全な電流は10mAです。 これは、トランジスタを焼損させない適切な電流量です。 そこで、エミッタ抵抗RE=VE/IEとし、VEはエミッタにかかる電圧、IEはエミッタに流れる電流を表します。 VE=VB-0.7V=5.65V となる。 ベース電圧とエミッタ電圧の差は、2つの接点間のダイオードの電圧降下だけです。 トランジスタはベースからエミッタまでダイオードが入っているため、内部で電圧降下が発生しているのです。 したがって、エミッタ電圧はベース電圧からダイオードの電圧降下を差し引いたものに等しくなります。 つまり、RE=VE/IE=5.65V/10mA=565Ωという式が成り立ちます。 ですから、この回路では500Ω程度のRE抵抗で十分なのです。
さて、最後にこの回路のコンデンサの値を選びます。 どちらのコンデンサも機能は同じです。 交流信号のみを通過させ、直流信号を遮断します。 つまり、カップリング・コンデンサとして機能するわけです。
まず、入力側のコンデンサの値を計算する方法を説明します。
コンデンサの適切な値を正しく選択するためには、これから説明する多くのことを考慮する必要があります。
一つは、回路のカットオフ周波数を決めることです。 これは、フィルタリングしてほしい周波数です。 音信号を扱う場合、人間に聞こえる周波数帯は20Hzから20,000Hzまでです。 可聴信号だけを通過させるトランジスタを作る場合、20Hzをカットオフ周波数に選ぶとよいでしょう。 つまり、その範囲以下の周波数はすべてフィルターにかけられ、グランドに落とされてしまうのです。 そこで、20Hzをカットオフ周波数として選択することにする。 20Hzを角周波数に当てはめると、ω=2πf≒125s-1となります。 これは式の一部です。
次に考えなければならないのは、コンデンサが見ている抵抗の値です。 この回路の最初の部分は、コンデンサとそれが見ている抵抗から接地まで、ハイパスフィルタ、RCハイパスフィルタを形成しています。 RCハイパスフィルタは、コンデンサと、グラウンドに接続された抵抗で構成される回路です。
回路に流れる電流を視覚化した場合、電流は3通りのうちどちらかに進みます。 電流はコンデンサーを通り、R2抵抗を通り、接地まで行くことができます。 コンデンサからR1抵抗に電流が流れる。 あるいは、トランジスタを通り、RE抵抗を通ってグランドに流れる。 R1抵抗に電流が流れるのは不思議に思えるかもしれませんが、AC信号はDC電圧レベルもグランドとして見ているのです。 つまり、(R1を通して)12VというDCレベルであっても、AC信号にとってはグランドでもあり、これがグランドへのパスにもなりうる理由です。
以上、3つの電流の流れ方があります。 電流はこれらの経路を通ることができますが、コンデンサが遭遇する実際の抵抗を決定するのは、最終的にはコンデンサが見ているものです。 ということで、今回はこの話をします。 抵抗R1、R2は並列です。 したがって、コンデンサには、この2つの並列抵抗の等価抵抗が見えています。 つまり、コンデンサは1KΩと1.1KΩの抵抗を並列に見ているわけです。 これらの抵抗の等価抵抗は、およそ500Ωです。 つまり、これはコンデンサが一方の経路で見ている抵抗値です。 もう1つの経路は、電流がトランジスタを通り、抵抗REを通過するときです。 この抵抗はβREとなる。 βが約100なので、この計算をすると、この抵抗は56KΩになります。
電流は常に最小抵抗の経路をとることを覚えておいてください。 つまり、500Ωと56KΩのどちらを選んでも、電流は明らかに500Ωの経路をとります。
つまり、500ΩはRCハイパスフィルタネットワークが見る等価抵抗で、カットオフ周波数は20Hzにしたいことが分かっています。 そして、20Hzの角周波数を計算すると、ω=2πf≈125s-1となります。
そこで、式にすると、REQC1=1/125s-1=(500Ω)C1=0.008sとなります。 計算すると、C1 の値は 16µF となります。 つまり、最初のコンデンサは16µFということになります。
次に、2つ目のコンデンサについて説明します。 これも1つ目のコンデンサと同様に選択する。
2番目のコンデンサーは、扱う周波数に関して、1番目のコンデンサーと同様の反応をするようにします。 これは、入力されたのと同じ周波数の信号が出力されるからです。 つまり、両方のコンデンサーの周波数応答を一致させたいのです。 そこで、出力側のコンデンサについても、20Hzの周波数特性に従って計算します。 角周波数を計算すると、再び、ω=2πf≈125s-1となります。
再び同じ式で、REQC2=1/125s-1とします。
この場合のREQは何でしょうか。 REQは、出力コンデンサが回路内で見る抵抗値です。 コンデンサから入力側に戻ってみると、コンデンサには (R1 || R2)/β= (1.1KΩ || 1KΩ)/100= (523Ω/100) ≒ 5Ωの抵抗が見えていることがわかります。 つまり、出力コンデンサは、回路の入力を振り返って5Ωの等価抵抗を見ることになる。
そこで、これらの値を式に突っ込むと、REQC2=1/125s-1= (5Ω)C2= 0.008s となる。 C2を解くと、1600μFとなります。 ということで、これが出力コンデンサの値です。
そして、これで回路内の部品の値をすべて解きました。
計算の結果、この回路は入力インピーダンスが高く、出力インピーダンスが低いことがわかります。 計算の結果、入力インピーダンスはβREで、56KΩと計算した。 出力インピーダンスは、5Ωと計算した。
この回路は、バッファリングが必要な電圧ラインに追加することができ、すべての電圧を転送することができる一方、負荷に電力を供給できるように低インピーダンス出力を提供することができる。 実際のバッファ・チップのような正確さはありません。 1つは、バッファ・チップはインピーダンスが大きく、出力インピーダンスが低いことです。 もう1つは、完全に正確なボルテージフォロワ回路ではありません。 トランジスタの内部にはダイオードがあり、その電圧降下はほぼ0に等しい。7Vになると、出力でこの電圧を失う。 つまり、出力信号は入力信号より0.7V低いのです。 つまり、完全なボルテージフォロアではないことがおわかりいただけると思います。
しかし、基本的な目的では、低精度のバッファとして非常によく機能します
。