Válasz 7 – 7 – 7 = 73 Ezt úgy olvassuk, hogy “hét kockával.”

Understanding Exponents and Square Roots

Learning Objective(s)

– Exponenseket tartalmazó kifejezések kiértékelése.

– Ismételt tényezők felírása exponenciális jelöléssel.

– Tökéletes négyzet négyzetgyökének megtalálása.

Az exponensek az ismételt szorzás írásának egy speciális módját biztosítják. Az így írt számoknak sajátos formájuk van, és minden egyes részük fontos információt ad a számról. A számok exponensekkel való írása sok helyet is megtakaríthat. Egy szám önmagával való szorzásának fordított műveletét a szám négyzetgyökének megtalálása. Ez a művelet hasznos a négyzet területével kapcsolatos problémáknál.

Az exponenciális jelölés az ismétlődő tényezők, például a 7 – 7 írásmódjának egy speciális módja. Az exponenciális jelölés két részből áll. A jelölés egyik részét bázisnak nevezzük. Az alap az a szám, amelyet megszorozunk önmagával. A jelölés másik része az exponens, vagyis a hatvány. Ez az a kis szám, amely a bázistól jobbra, magasra van írva. Az exponens vagy hatvány megmondja, hogy a szorzás során hányszor kell a bázist tényezőként használni. A példában a 7 – 7-et 72-nek lehet írni, 7 a bázis, 2 pedig az exponens. A 2 exponens azt jelenti, hogy két tényező van.

72 = 7 – 7 = 49

A 72-t úgy is olvashatod, hogy “hét négyzet”. Ez azért van, mert egy szám önmagával való megszorzását “szám négyzetre emelésének” nevezik. Hasonlóképpen, egy szám felemelését 3 hatványára úgy hívják, hogy “a szám felkockázása”. A 73-at úgy is olvashatod, hogy “hét a négyzetben.”

A 25-öt úgy is olvashatod, hogy “kettő az ötödik hatványra” vagy “kettő az ötödik hatványára”. A 84-et úgy olvashatod, mint “nyolc a negyedik hatványra” vagy “nyolc a négy hatványára”. Ez a formátum bármely exponenciális jelöléssel írt szám olvasására használható. Valójában, bár a 63-at leggyakrabban úgy olvassák, hogy “hat kocka”, de olvasható “hat a harmadik hatványra” vagy “hat a három hatványára” is.

Az exponenciális formában írt szám értékének megkereséséhez írjuk át a számot ismételt szorzásként, és végezzük el a szorzást. Az alábbiakban két példát mutatunk.

Keresd meg a 43 értékét.

A) 12

B) 64

C) 256

D) 43

Az ismételt szorzás exponenciális jelöléssel való írása időt és helyet takaríthat meg. Tekintsük az 5 – 5 – 5 – 5 – 5 példát. Ezt az ismételt szorzást exponenciális jelöléssel 54-nek írhatjuk. Mivel az 5-öt szorozzuk, ezért azt írjuk bázisként. Mivel a bázist négyszer használjuk a szorzás során, az exponens 4. Az 5 – 5 – 5 – 5 – 5 kifejezés rövidített exponenciális jelöléssel átírható 54-re, és így olvasható: “öt a negyedik hatványra” vagy “öt a 4 hatványára.”

Az azonos szám ismételt szorzásának exponenciális jelöléssel történő leírásához először a szorzott számot írjuk bázisként. Ezután számold meg, hányszor szerepel ez a szám a szorzásban, és írd ezt a számot exponensként. Ügyeljen arra, hogy az exponens meghatározásához a számokat számolja, ne a szorzás jeleit.

Írd le 10 – 10 – 10 – 10 – 10 – 10 – 10 – 10 exponenciális jelöléssel.

A) 1,000,000

B) 60

C) 105

D) 106

Amint korábban láttad, az 52-t “öt négyzetnek” nevezik. Az “öt négyzete” azt jelenti, hogy ötöt megszorozzuk önmagával. A matematikában egy szám önmagával való megszorzását a szám négyzetre szorzásának nevezzük. Egy egész szám négyzetelésének eredményét négyzetnek vagy tökéletes négyzetnek nevezzük. Tökéletes négyzetnek nevezünk minden olyan számot, amely felírható egész számként 2 hatványára emelve. Például a 9 tökéletes négyzet. A tökéletes négyzet alakú számot négyzet alakban ábrázolhatjuk, ahogy az alábbiakban látható. Láthatjuk, hogy az 1, 4, 9, 16, 25 és 36 példák a tökéletes négyzetekre.

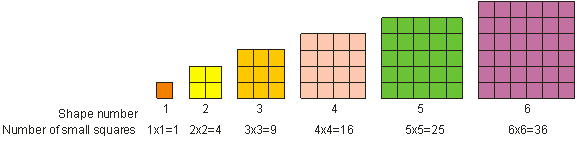
A szám négyzetbe állításához szorozzuk meg a számot önmagával. A 3 négyzet = 32 = 3 – 3 = 9.

Az alábbiakban további példákat találsz a tökéletes négyzetekre.

A szám négyzetre számolásának fordított műveletét a szám négyzetgyökének megtalálása. A négyzetgyök megtalálása olyan, mintha azt kérdeznénk, hogy “melyik számot megszorozva önmagával kapom ezt a számot?”. A 25 négyzetgyöke 5, mert 5 szorozva önmagával egyenlő 25-tel. A négyzetgyököket a gyökjelnek nevezett matematikai szimbólummal írjuk le, amely így néz ki: . A “25 négyzetgyökét” így írjuk: .

Keresd .

A) 6

B) 18

C) 72

D) 7

Az exponenciális jelölés egy rövidített módja az azonos szám ismételt szorzásának. Az exponenciális jelöléssel írt számnak van egy bázisa és egy exponense, és ezek mindegyike információt szolgáltat a kifejezés értékének megtalálásához. A bázis megmondja, hogy milyen számot szorozunk ismételten, az exponens pedig azt, hogy a szorzás során hányszor használjuk fel a bázist. A 2-es és 3-as exponenseknek különleges nevük van. A bázis 2-es hatványra emelését a szám “négyzetre emelésének” nevezik. A bázis 3-as hatványra emelését a szám “felkockázásának” nevezzük. A szám négyzetre emelésének fordítottja a szám négyzetgyökének megtalálása. Ha meg akarod találni egy szám négyzetgyökét, kérdezd meg magadtól: “Milyen számot tudok megszorozni önmagával, hogy megkapjam ezt a számot?”