
The Policy Question: Hibridautó-vásárlási adókedvezmény-ez a kormány legjobb választása az üzemanyag-fogyasztás és a szén-dioxid-kibocsátás csökkentésére?
Az Egyesült Államok lakosai és a kormány aggódik az importált külföldi olajtól való függőség és a légkörbe kerülő szén-dioxid-kibocsátás miatt. 2005-ben a Kongresszus törvényt fogadott el, hogy a fogyasztóknak adókedvezményt nyújtson az elektromos és hibrid autók vásárlásához.
Ez az adókedvezmény jó politikai döntésnek tűnhet, de költséges, mert közvetlenül csökkenti az amerikai kormány által beszedett bevételek összegét. Vannak-e hatékonyabb megközelítések a fosszilis tüzelőanyagoktól való függőség és a szén-dioxid-kibocsátás csökkentésére? Hogyan döntsük el, hogy melyik politika a legjobb? E kérdés megválaszolásához a politikai döntéshozóknak bizonyos pontossággal meg kell jósolniuk, hogy a fogyasztók hogyan fognak reagálni erre az adópolitikára, mielőtt ezek a politikai döntéshozók szövetségi dollármilliókat költenének.
A hasznosság fogalmát alkalmazhatjuk erre a politikai kérdésre. Ebben a modulban a hasznosságot és a hasznossági függvényeket fogjuk tanulmányozni. Ezután képesek leszünk egy megfelelő hasznossági függvényt használni a szakpolitikai kérdésünket leíró közömbösségi görbék levezetéséhez.
A szakpolitikai kérdés vizsgálata
Tegyük fel, hogy a hibrid autók vásárlását támogató adókedvezmény rendkívül sikeres, és megduplázza az Egyesült Államok útjain közlekedő összes autó átlagos üzemanyag-fogyasztását – ez az eredmény nyilvánvalóan nem reális, de hasznos a későbbi vitáinkhoz. Ön szerint mi történne az összes amerikai autós üzemanyag-fogyasztásával? Elvárhatná-e a kormány, hogy válaszul az autók üzemanyag-fogyasztása és szén-dioxid-kibocsátása a felére csökkenjen? Miért vagy miért nem?
2.1 Haszonfüggvények
LO 2.1: Írja le a hasznossági függvényt.
2.2 Haszonfüggvények és tipikus preferenciák
LO 2.2: Azonosítsa a hasznossági függvényeket az általuk képviselt tipikus preferenciák alapján.
2.3 A hasznossági függvények és a közömbösségi görbék térképének összefüggése
LO 2.3: Magyarázza el, hogyan lehet egy közömbösségi görbét levezetni egy hasznossági függvényből.
2.4 Határhaszon és határhelyettesítési ráta megállapítása
LO 2.4: Vezesse le a határhaszon és az MRS tipikus hasznossági függvényekre.
2.5. Politikai kérdés
2.1. Haszonfüggvények
LO1: Írjon le egy hasznossági függvényt.
A preferenciáink lehetővé teszik számunkra, hogy összehasonlításokat végezzünk különböző fogyasztási csomagok között, és kiválasszuk a preferált csomagokat. Preferenciáink alapján meghatározhatjuk például egy egész halmaznyi köteg rangsorát. A hasznossági függvény egy olyan matematikai függvény, amely a fogyasztási javak kötegeit egy-egy szám hozzárendelésével rangsorolja, ahol a nagyobb számok a preferált kötegeket jelzik. A hasznossági függvények rendelkeznek azokkal a tulajdonságokkal, amelyeket az 1. modulban a preferenciákkal kapcsolatban azonosítottunk. Azaz: képesek a kötegek rendezésére, teljesek és tranzitívak, a többet előnyben részesítik a kevesebbel szemben, és releváns esetekben a vegyes kötegek jobbak.
A számot, amelyet a hasznossági függvény egy adott köteghez rendel, hasznosságnak nevezzük, vagyis azt az elégedettséget, amelyet a fogyasztó egy adott kötegből nyer. Az egyes kötegekhez tartozó hasznossági szám abszolút értelemben nem jelent semmit; nincs egységes skála, amelyhez képest az elégedettséget mérnénk. Csak relatív értelemben van értelme: a hasznosságot arra használhatjuk, hogy meghatározzuk, mely kötegeket részesítjük előnyben másokkal szemben.
Ha az A köteg hasznossága nagyobb, mint a B kötegé, akkor ez egyenértékű azzal, hogy a fogyasztó az A köteget részesíti előnyben a B köteggel szemben.A hasznossági függvények ezért a fogyasztói preferenciákat úgy rangsorolják, hogy minden köteghez egy számot rendelnek. . A hasznossági függvényt használhatjuk az 1. modulban ismertetett közömbösségi görbe leképezéséhez. Mivel ugyanazon a közömbösségi görbén minden köteg ugyanazt a kielégülést nyújtja, és ezért egyik sem preferált, minden kötegnek ugyanaz a hasznossága. Ezért a közömbösségi görbét úgy rajzolhatjuk meg, hogy meghatározzuk az összes olyan köteget, amely a hasznossági függvényből ugyanazt a számot adja vissza.
A közgazdászok azt mondják, hogy a hasznossági függvények inkább ordinálisak, mint kardinálisak. Az ordinális azt jelenti, hogy a hasznossági függvények csak rangsorolják a kötegeket – csak azt jelzik, hogy melyik a jobb, azt nem, hogy mennyivel jobb, mint egy másik köteg. Tegyük fel például, hogy egy hasznossági függvény azt jelzi, hogy az A köteg 10 hasznosságot, a B köteg pedig 20 hasznosságot ad. Nem mondjuk, hogy a B köteg kétszer olyan jó, vagy 10 hasznossal jobb, csak azt, hogy a fogyasztó a B köteget részesíti előnyben. Tegyük fel például, hogy egy barátunk benevezett egy versenyre, és azt mondta, hogy harmadik lett. Ez az információ ordinális: Tudja, hogy gyorsabb volt, mint a negyedik helyezett, és lassabb, mint a második helyezett. Ön csak azt tudja, hogy a futók milyen sorrendben értek célba. Az egyéni idők kardinálisak: Ha az első helyezett pontosan egy óra alatt futotta le a versenyt, a barátod pedig egy óra hat perc alatt ért célba, akkor tudod, hogy a barátod pontosan 10%-kal volt lassabb, mint a leggyorsabb futó. mivel a hasznossági függvények ordinálisak, sok különböző hasznossági függvény képviselheti ugyanazokat a preferenciákat. Ez mindaddig igaz, amíg a sorrendiség megmarad.
Vegyük például az U hasznossági függvényt, amely az A és B javak kötegei feletti preferenciákat írja le: U(A,B). Bármilyen pozitív monoton transzformációt alkalmazhatunk erre a függvényre (ami lényegében azt jelenti, hogy nem változtatjuk meg a sorrendet), és az általunk létrehozott új függvény ugyanazokat a preferenciákat fogja reprezentálni. Például megszorozhatunk egy pozitív állandót, α , vagy hozzáadhatunk egy pozitív vagy egy negatív állandót, β . Tehát αU(A,B)+β pontosan ugyanazokat a preferenciákat reprezentálja, mint U(A,B), mert pontosan ugyanúgy fogja rendezni a kötegeket. Ez a tény igen hasznos, mert néha egy hasznossági függvény pozitív monoton transzformációjának alkalmazása megkönnyíti a problémák megoldását.
2.2. Haszonfüggvények és tipikus preferenciák
LO2: Haszonfüggvények azonosítása az általuk reprezentált tipikus preferenciák alapján
Lássuk az almából, A, és banánból, B, álló kötegeket. Az Isaac almából és banánból álló kötegekkel kapcsolatos preferenciáit leíró hasznossági függvény az U(A,B) függvény. De mik Isaac konkrét preferenciái az alma- és banánkötegekkel kapcsolatban? Tegyük fel, hogy Isaacnak meglehetősen standard preferenciái vannak az almával és a banánnal kapcsolatban, amelyek a mi tipikus közömbösségi görbéinkhez vezetnek: Jobban szereti a többet, mint a kevesebbet, és szereti a változatosságot. Az ezeket a preferenciákat reprezentáló hasznossági függvény lehet:
U(A,B) = AB
Ha az alma és a banán tökéletes komplementerek Isaac preferenciáiban, akkor a hasznossági függvény valahogy így nézne ki:
U(A,B) = MIN,
ahol a MIN függvény egyszerűen a két szám közül a kisebbet jelöli ki a függvény értékeként.
Ha az alma és a banán tökéletes helyettesítői egymásnak, akkor a hasznossági függvény additív, és valahogy így nézne ki:
U(A,B) = A + B
A közgazdaságtanban két okból nagyon gyakran használják a Cobb-Douglas hasznossági függvények egy osztályát:
1. Olyan “jól viselkedő” preferenciákat reprezentálnak, mint például a több jobb és a változatosság preferálása.
2. Nagyon rugalmasak, és nagyon könnyen hozzáigazíthatók a valós adatokhoz.
A Cobb-Douglas hasznossági függvények ilyen alakúak:
U(A,B) = AαBβ
Mivel a pozitív monoton transzformációk ugyanazokat a preferenciákat reprezentálják, egy ilyen transzformációval α + β = 1 , amit később látni fogunk, hogy ez egy kényelmes feltétel, ami leegyszerűsít néhány matematikai feladatot a fogyasztói választási problémában.
Egy másik módja a hasznossági függvény hasznos átalakításának, ha a függvény természetes logaritmusát vesszük, ami egy új függvényt hoz létre, amely így néz ki:
U(A,B) = αln(A) + βln(B)
Az egyenlet levezetéséhez egyszerűen alkalmazzuk a természetes logaritmus szabályait . Fontos szem előtt tartani itt az absztrakciós szintet. Általában nem tudunk olyan konkrét hasznossági függvényeket készíteni, amelyek pontosan leírják az egyéni preferenciákat. Valószínűleg egyikünk sem tudná egyetlen egyenlet segítségével leírni saját preferenciáit. De mindaddig, amíg a fogyasztók preferenciái általában véve követik az alapfeltevéseinket, elég jó munkát végezhetünk a valós fogyasztási adatoknak megfelelő hasznossági függvények megtalálásával. Ennek bizonyítékát a kurzus későbbi részében látni fogjuk.
A 2.1. táblázat összefoglalja az ebben a fejezetben ismertetett preferenciákat és hasznossági függvényeket.
|
A 2. táblázat.1 A preferenciák típusai és az őket reprezentáló hasznossági függvények |
||
|
PREFERENCIÁK |
HASZNÁLATI FUNKCIÓK FUNKCIÓ |
HASZNÁLATI FUNKCIÓ TÍPUSA |
|
Változatosságszeretet vagy “jólneveltség” |
U(A,B) = AB |
Cobb-Douglas |
|
Változatosságszeretet vagy “jól nevelt” |
U(A,B) = AαBβ |
Cobb-Douglas |
|
Változatosságszeretet vagy “jól nevelt” |
U(A,B) = αln(A) + βln(B) |
Természetes log Cobb-Douglas |
|
Tökéletes kiegészítések |
U(A,B) = MIN |
Min Function |
|
Perfect Substitutes |
U(A,B) = A + B |
Additív |
2.3 Haszonfüggvények és közömbösségi görbék térképek egymáshoz való viszonyítása
LO3: Magyarázza meg, hogyan lehet egy közömbösségi görbét levezetni egy hasznossági függvényből
A közömbösségi görbék és a hasznossági függvények közvetlen kapcsolatban állnak egymással. Mivel a közömbösségi görbék grafikusan, a hasznossági függvények pedig matematikailag ábrázolják a preferenciákat, ebből következik, hogy a közömbösségi görbék levezethetők a hasznossági függvényekből.
Az egyváltozós függvényeknél a függő változót a függőleges tengelyen, a független változót pedig a vízszintes tengelyen ábrázoljuk, mint az y=f(x) grafikonján. Ezzel szemben a kétváltozós függvények grafikonjai háromdimenziósak, mint például az U=U(A,B). A 2.1. ábra az U=A^\frac{1}{2}B^\frac{1}{2} grafikonját mutatja. A háromdimenziós grafikonok hasznosak annak megértéséhez, hogy hogyan nő a hasznosság A és B fogyasztásának növekedésével.
2.1. ábra U=A^\frac{1}{2}B^\frac{1}{2}
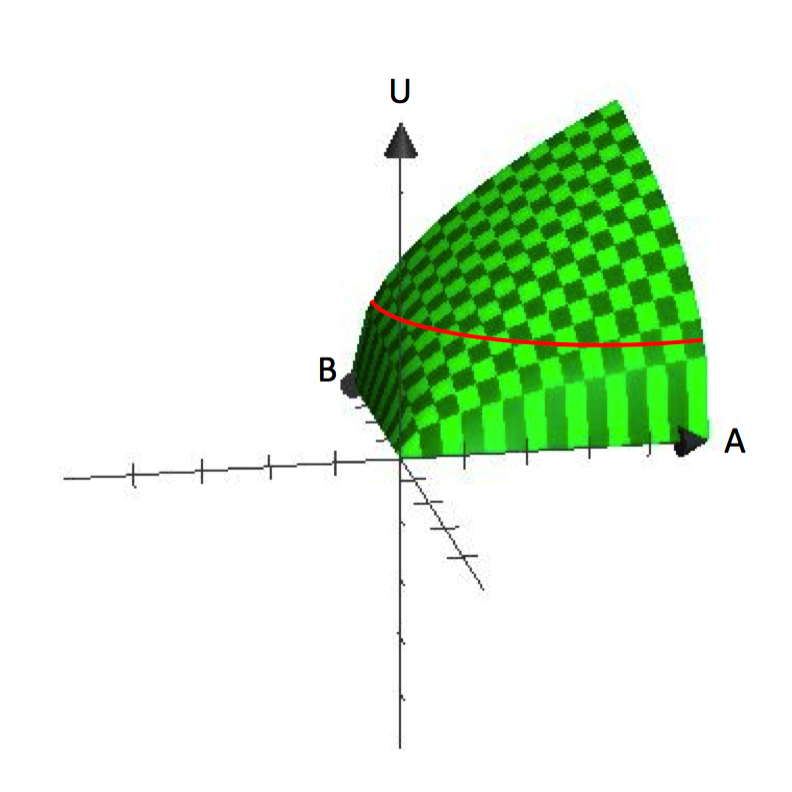
A 2.1. ábrán jól látható az a feltételezés, hogy a fogyasztók a változatosságot preferálják. Minden köteg, amely meghatározott mennyiségű A-t és B-t tartalmaz, egy pontot képvisel a felületen. A felület függőleges magassága a hasznossági szintet jelenti. Mind A, mind B növelésével a fogyasztó magasabb pontokat érhet el a felszínen.
Honnan származnak tehát a közömbösségi görbék? Emlékezzünk vissza, hogy a közömbösségi görbe azon csomagok összessége, amelyekkel kapcsolatban a fogyasztó közömbös, hogy melyiket fogyasztja. Matematikailag ez egyenértékű azzal, hogy a hasznossági függvénybe helyezve minden csomag ugyanazt a funkcionális értéket adja vissza. Ha tehát megadunk egy Ū értéket a hasznosságnak, és megkeressük az összes olyan A és B csomagot, amely ezt az értéket adja, akkor egy közömbösségi görbét fogunk definiálni. Vegyük észre, hogy ez egyenértékű azzal, hogy megtaláljuk az összes olyan köteget, amelyekkel a fogyasztó a 2.1. ábrán látható háromdimenziós felületen ugyanarra a magasságra jut.
A közömbösségi görbék a magasságot (hasznossági szintet) ábrázolják egy sík felületen. Ily módon analógok a topográfiai térképen lévő szintvonallal. Ha a háromdimenziós grafikont visszavezetjük a kétdimenziós térbe – az A, B térbe -, akkor megmutathatjuk a különböző magasságokat vagy hasznossági szinteket ábrázoló szintvonalakat/különbséggörbéket. A 2.1. ábrán látható grafikonon már látható, hogy ez a hasznossági függvény olyan közömbösségi görbéket eredményez, amelyek az origó felé “behajlítottak” vagy homorúak.
A közömbösségi görbék tehát közvetlenül a hasznossági függvényekből következnek, és hasznos módja a hasznossági függvények kétdimenziós grafikonon való ábrázolásának.
2.4 A határhaszon és a határhelyettesítési ráta meghatározása
LO4: A határhaszon és az MRS származtatása tipikus hasznossági függvényekre.
A határhaszon az a többlethasznosság, amelyet a fogyasztó egy áru egy további egységének fogyasztásából kap. Matematikailag ezt a következőképpen fejezzük ki:
MU_{a}=\frac{\Delta \cup }{\Delta A}
vagy a fogyasztott A mennyiségének változásából származó hasznosság változása, ahol Δ a tétel értékének változását jelenti. Tehát,
MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}
Megjegyezzük, hogy amikor A fogyasztásának határhasznosságát vizsgáljuk, B-t állandónak tartjuk.
A számtan segítségével a határhaszon megegyezik a hasznossági függvény A-ra vonatkozó parciális deriváltjával:
MU_{A}\frac{\parciális U(A,B)}{\parciális A}
Gondoljunk egy fogyasztóra, aki leül egy salátából és pizzából álló étkezéshez. Tegyük fel, hogy a saláta mennyiségét állandónak tartjuk – például egy köret saláta a vacsorához. Most növeljük a pizzaszeletek számát tegyük fel, hogy 1 szelettel a hasznosság 10, 2-vel 18, 3-mal 24 és 4-gyel 28. Ábrázoljuk ezeket a számokat egy olyan grafikonon, amelynek függőleges tengelyén a hasznosság, vízszintes tengelyén pedig a pizza van (2.2. ábra).
2.2. ábra: A csökkenő határhasznosság grafikonja és táblázata
|
Pizzaszeletek |
Hasznosság |
Marginalis Hasznosság |
|
|
1 |
10 |
|
|
|
2 |
18 |
8 |
|
|
3 |
24 |
6 |
|
|
4 |
28 |
4 |
|
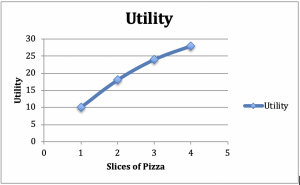
A grafikon pozitív meredekségéből, láthatjuk a további szelet pizza hasznosságának növekedését. A grafikon homorú alakjából egy másik általános jelenséget láthatunk: Az a többlethaszon, amelyet a fogyasztó minden egyes további szelet pizzából kap, az elfogyasztott szeletek számával csökken.
Azt a tényt, hogy a többlethaszon minden egyes további szelet pizzával kisebb lesz, a csökkenő határhaszon elvének nevezzük. Ez az elv jól viselkedő preferenciákra vonatkozik, ahol a vegyes csomagok előnyben részesülnek.
A helyettesítés határrátája (MRS) az a mennyiség, amelyről a fogyasztó hajlandó lemondani, hogy egy másik termékből egy egységgel többet kapjon. Ezért azonos a közömbösségi görbe meredekségével – mivel az elégedettségi szintet állandóan tartjuk, ugyanazon a közömbösségi görbén maradunk, csak mozgunk rajta, ahogy az egyik jószágot egy másikra cseréljük. Az, hogy az egyikből mennyit vagyunk hajlandóak elcserélni egy másikból eggyel többért, attól függ, hogy mekkora a határhaszonunk mindkettőből.
A korábbi példánkat használva, ha eggyel több oldalsaláta fogyasztásával a hasznosságunk 10-tel nő, akkor a jelenlegi 4 szelet pizza fogyasztása mellett lemondhatunk 2 szelet pizzáról, és 28-ról 18-ra csökken a hasznosságunk. Ha 10 hasznossal többet kapunk a salátától, és 10 hasznossal kevesebbet a 2 szelet pizzáról való lemondással, az összhaszon változatlan marad – tehát még mindig ugyanazon a közömbösségi görbén kell lennünk. Ahogy a közömbösségi görbén haladunk, a lejtőn kell lovagolnunk, vagyis a függőleges tengelyen lévő jószágról kell lemondanunk a vízszintes tengelyen lévő jószágból többért, ami negatív emelkedést eredményez egy pozitív futás során.
A két fogalom közötti kapcsolat felismerésével a határhaszonról közvetlenül áttérhetünk az MRS-re. Esetünkben egy U=U(A,B) hasznossági függvény esetében az MRS a következőképpen ábrázolható:
MRS=-\frac{MU_{A}}{MU_{B}}
Megjegyezzük, hogy ha helyettesítjük, egyszerűsíthetjük az egyenletet:
MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{\frac{\frac{\Delta U}{\Delta A}}}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}
Az egyenletet beillesztve ez az egyenlet a következő::
MRS=-\frac{\frac{\frac{\partial U(A,B)}{\partial A}}{\frac{\partial U(A,B)}{\partial B}}
2.5 Szakpolitikai kérdés
Az 1. modulban megállapítottuk, hogy a több megtett kilométer és az egyéb fogyasztás közötti releváns fogyasztói döntés valószínűleg megfelel a fogyasztói választásra vonatkozó standard feltevéseknek. Ezért jó választás a Cobb-Douglas hasznossági függvényt használni egy olyan fogyasztó ábrázolására, aki szeret autót vezetni és más javakat is fogyasztani, és aki ezeket kompromisszumnak tekinti (a benzinre költött pénz más fogyasztási javakra el nem költött pénz). Előnye továbbá, hogy egyrészt megfelel a feltételezéseknek, másrészt rugalmas:
U(MD,C)=MD^{a}C^{\beta } ,
mivel MD = megtett kilométerek, és C = egyéb fogyasztás.
Sőt, maga a függvény valós adatokra vihető, ahol a paraméterek és becsülhetők erre a piacra, a fogyasztó autójával megtett kilométerek piacára.
2.3. ábra A közömbösségi görbék grafikonja a politikai példára
A politikai kérdések feltárása:
1 . Más preferenciatípusok megfelelőbbek lennének ebben a példában?
2. Minek kellene igaznak lennie ahhoz, hogy a tökéletes komplementer legyen a megfelelő preferenciatípus ennek a politikának az elemzéséhez?
Minek kellene igaznak lennie a tökéletes helyettesítőhöz? Tekintettel arra, hogy egy “tipikus” fogyasztóról van szó, aki autóval közlekedik, helyénvaló-e “tipikus” hasznossági függvényt választani?
4. Csak találgatunk, vagy van valamilyen elméleti alapunk a “jól viselkedő” preferenciák vagy a Cobb-Douglas hasznossági függvény választásának alátámasztására?
ÖSSZEGZÉS
Áttekintés: Témák és kapcsolódó tanulási eredmények
2.1 Hasznossági függvények
LO 2.1: Haszonfüggvények leírása
2.2 Haszonfüggvények és tipikus preferenciák
LO 2.2: Határozza meg a hasznossági függvényeket az általuk képviselt tipikus preferenciák alapján
2.3 A hasznossági függvények és a közömbösségi görbék térképének összefüggése
LO 2.3: Magyarázza el, hogyan vezethető le egy közömbösségi görbe egy hasznossági függvényből
2.4 Határhaszon és határhelyettesítési ráta meghatározása
LO 2.4: Vezesse le a határhaszon és az MRS-t tipikus hasznossági függvényekre
2.5. Válassza le a határhaszon és az MRS-t. Politikai kérdés
Learn: Kulcsfogalmak és grafikonok
Bi-variánsfüggvények
Kardinális
Kontúrvonal
csökkenő határhaszon
Függvény
Marginal rate of substitution (MRS)
Marginal utility
Ordinális
Univariate functions
Util
Utility
Utility function
Graphs
3D utility function and contour line
Equations
Cobb-Douglas
Tökéletes kiegészítések
Tökéletes helyettesítések