Ebben a leckében egy egyszerű stratégiát mutatunk a következő feladat megoldására: hogyan találjuk meg egy egyenlő szárú háromszög területét.
Az eddig bizonyított tulajdonságok egy részét a gyakorlatban is alkalmazzuk a következő geometriai feladatban:
Probléma
Egy 10 láb hosszúságú ΔABC nevű egyenlő szárú háromszögben az alap magassága az alap kétharmadával egyenlő. Keressük meg a háromszög területét.
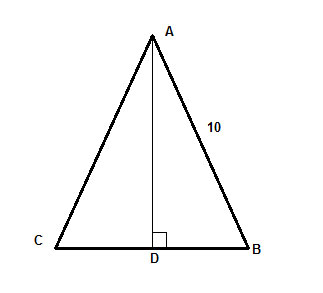
Stratégia
A feladat megoldásához visszafelé fogunk dolgozni, hogy mit kell tennünk.
Meg kell találnunk a háromszög területét, amit tudjuk, hogy a (alap szorozva a magassággal)/2 képlet ad meg.
Egy problémánk az, hogy nem tudjuk sem az alap hosszát, sem a magasságát. De meg van adva a köztük lévő kapcsolat, ami a támpont arra, hogy mit kell tennünk. Nevezzük az alap, BC hosszát x-nek.
Ezután tudjuk, hogy a magasság, AD, 2x/3, ahogy a feladatban is szerepel.
A válasz, amit keresünk, tehát (alap szorozva magassággal)/2, vagy x szorozva 2x/3, osztva kettővel.
De hogyan találjuk meg az x-et? Két további dolgot kaptunk a feladatban, amit még nem használtunk fel – a láb hosszát (10), és azt, hogy ez egy egyenlő szárú háromszög. Valószínűleg ezt a két dolgot kell használnunk a feladat megoldásához.
Megnézzük az egyenlő szárú háromszögek tulajdonságait. Az egyik dolog, ami azonnal eszünkbe kell, hogy jusson, hogy mint már megmutattuk, egy egyenlő szárú háromszögben az alap magassága felezi az alapot, tehát CD=DB=x/2.
Végül AD a magasság, ami azt jelenti, hogy a ∠ADC szög derékszög, és van egy derékszögű háromszögünk, ΔADC, amelynek hipotenzusát ismerjük (10), és a Pitagorasz-tétel segítségével meg tudjuk találni a lábakat, c2 =a2+b2,
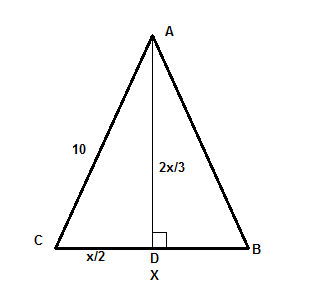
ahol c=10 ,a=x/2 és b=2x/3 . És kész is vagyunk, a többi már csak az x algebrai megoldása.
Bizonyítás: Egy egyenlő szárú háromszög területe
(1) ΔADC derékszögű háromszög //adva, mivel AD az alap magassága
(2) AC2 =CD2 + AD2 //Pythagorasz-tétel
(3) AC= 10 //adva
(4) CB = x
(5) CD = x/2 //Az egyenlő szárú háromszög alapjának magassága felezi az alapot
(6) AD = 2x/3 //adva
(7) 102 = (x/2)2 + (2x/3)2 //helyettesítve (2)-be
(8) 100 = x2/4+4×2/9 //egyszerűsítve
(9) 100*36 = 9×2 +16×2 // mindkét oldalt megszorozzuk 36-tal
(10) 100*36 = 25×2 //összeszedjük a hasonló kifejezéseket
.