A modern audio korban a “Hi-Res” és a 24 bites “Studio Quality” zene említésére már nem mozdulhatsz. Ha még nem vette észre a trendet a csúcskategóriás okostelefonokban – a Sony LDAC Bluetooth-kódkódját – és az olyan streaming-szolgáltatásokban, mint a Tidal, akkor tényleg többet kellene olvasnia ezt az oldalt.
Az ígéret egyszerű – kiváló hallgatási minőség a több adatnak, azaz a bitmélységnek köszönhetően. Ez 24 bit digitális egyeseket és nullákat jelent, szemben a CD-korszakból származó 16 bites másnapossággal. Természetesen ezekért a jobb minőségű termékekért és szolgáltatásokért felárat kell fizetni, de a több bit biztosan jobb, nem?
A “alacsony felbontású” hangot gyakran lépcsőzetes hullámformaként mutatják be. A hangmintavételezés nem így működik, és nem így néz ki a készülékből kijövő hang.
Nem feltétlenül. Az egyre nagyobb és nagyobb bitmélységek iránti igény nem a tudományos valóságon alapul, hanem inkább az igazság kiforgatásán és a hang tudományával kapcsolatos fogyasztói tájékozatlanság kihasználásán. Végső soron a 24 bites hangot forgalmazó cégeknek sokkal több hasznuk van a profitból, mint Önnek a kiváló lejátszási minőségből.
Bitmélység és hangminőség: A lépcsőzés nem egy dolog
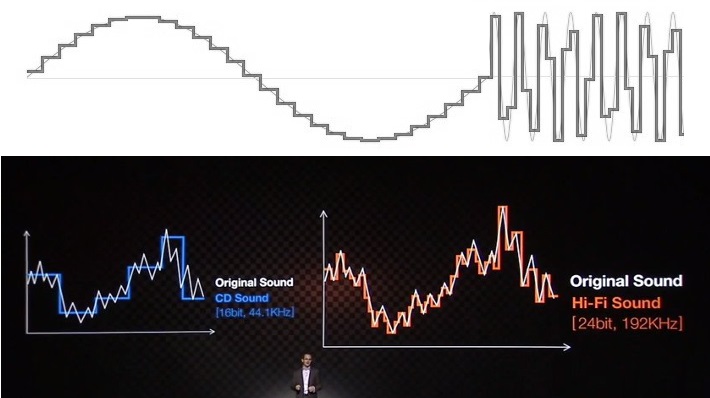
Azért, hogy azt sugallják, hogy a 24 bites hangzás kötelezően szükséges, a cégek (és túl sokan mások, akik megpróbálják elmagyarázni ezt a témát) a nagyon jól ismert hangminőségi lépcsőzést tálalják. A 16 bites példa mindig egy szinuszhullám vagy más jel döcögős, szaggatott reprodukcióját mutatja, míg a 24 bites megfelelője gyönyörűen simának és nagyobb felbontásúnak tűnik. Ez egy egyszerű vizuális segédeszköz, amely azonban a témában és a tudományban való járatlanságra támaszkodik, hogy a fogyasztókat téves következtetésekre vezesse.
Mielőtt valaki leharapná a fejemet, technikailag ezek a lépcsőzetes példák némileg pontosan ábrázolják a digitális tartományban a hangot. Azonban egy stem plot/lollipop diagram pontosabb grafika a vizuális hangmintavételezéshez, mint ezek a lépcsőfokok. Gondoljon erre így – egy minta egy nagyon konkrét időpontban lévő amplitúdót tartalmaz, nem pedig egy meghatározott ideig tartott amplitúdót.

A lépcsős grafikonok használata szándékosan félrevezető, amikor a stem-diagramok pontosabb ábrázolást nyújtanak a digitális hangról. Ez a két grafikon ugyanazokat az adatpontokat ábrázolja, de a lépcsődiagram sokkal kevésbé tűnik pontosnak.
Mégis igaz, hogy egy analóg-digitális átalakítónak (ADC) végtelen számú analóg audiojelet kell véges számú bitbe illesztenie. A két szint közé eső bitet a legközelebbi közelítésre kell kerekíteni, amit kvantálási hibának vagy kvantálási zajnak nevezünk. (Ezt jegyezzük meg, mert még visszatérünk rá.)
Ha azonban megnézzük bármelyik, ebben az évszázadban (és valószínűleg jóval korábban) gyártott digitális-analóg átalakító (DAC) hangkimenetét, nem fogunk lépcsőfokokat észrevenni. Még akkor sem, ha 8 bites jelet ad ki. Akkor mi a helyzet?

Egy olcsó Pixel 3a okostelefonból rögzített 8 bites, 10 kHz-es szinuszhullám kimenet. Láthatunk némi zajt, de nincsenek észrevehető lépcsőfokok, amelyeket az audiocégek oly gyakran ábrázolnak.
Először is, amit ezek a lépcsőfokdiagramok leírnak, ha egy hangkimenetre alkalmazzuk őket, az egy úgynevezett nulla sorrendtartású DAC. Ez egy nagyon egyszerű és olcsó DAC-technológia, ahol a jelet minden új mintánál átkapcsolják a különböző szintek között, hogy kimenetet adjanak. Ezt egyetlen professzionális vagy félig-meddig tisztességes fogyasztói audio termékben sem használják. Talán egy 5 dolláros mikrokontrollerben megtalálható, de máshol biztosan nem. A hangkimenetek ilyen módon való téves ábrázolása torz, pontatlan hullámformát feltételez, de nem ezt kapod.

A valóságban egy modern ∆Σ DAC kimenete egy túlmintavételezett 1 bites PDM jel (jobbra), nem pedig egy nulla tartású jel (balra). Ez utóbbi szűréssel alacsonyabb zajszintű analóg kimenetet eredményez.
A hangminőségű ADC-k és DAC-k túlnyomórészt delta-szigma (∆Σ) moduláción alapulnak. Az ilyen kaliberű komponensek közé tartozik az interpoláció és a túlmintavételezés, a zajformázás és a szűrés a zaj kisimítására és csökkentésére. A delta-szigma DAC-ok a hangmintákat 1 bites folyamattá alakítják (impulzus-sűrűség moduláció), nagyon magas mintavételi sebességgel. Szűréssel ez sima kimeneti jelet eredményez, amelynek zaja jóval a hallható frekvenciákból kiszorul.
Dióhéjban: a modern DAC-ok nem durva kinézetű, szaggatott hangmintákat adnak ki – egy olyan bitfolyamot adnak ki, amelyet zajszűréssel nagyon pontos, sima kimenetté alakítanak. Ez a lépcsőzetes megjelenítés a “kvantálási zajnak” nevezett valami miatt rossz.”
A kvantálási zaj megértése
Minden véges rendszerben előfordulnak kerekítési hibák. Igaz, hogy egy 24 bites ADC vagy DAC kisebb kerekítési hibával rendelkezik, mint egy 16 bites megfelelője, de mit is jelent ez valójában? És ami még fontosabb, mit is hallunk valójában? Ez torzítás vagy fuzz, a részletek örökre elvesznek?
Valójában egy kicsit mindkettő, attól függően, hogy a digitális vagy az analóg birodalomban vagyunk. De a kulcsfogalom mindkettő megértéséhez a zajszint megismerése, és hogy ez hogyan javul a bitmélység növekedésével. A szemléltetés érdekében lépjünk vissza a 16 és 24 bitektől, és nézzünk meg nagyon kis bitmélységű példákat.
A 16 és 24 bitmélység közötti különbség nem a hullámforma alakjának pontossága, hanem az elérhető határ, mielőtt a digitális zaj zavarja a jelünket.
Az alábbi példában elég sok mindent meg kell vizsgálnunk, ezért először egy gyors magyarázatot adunk arról, hogy mit is nézünk. A felső ábrákon a bemeneti (kék) és a kvantált (narancssárga) hullámformáinkat látjuk, 2, 4 és 8 bites bitmélységgel. Egy kis zajt is adtunk a jelünkhöz, hogy jobban szimuláljuk a valós világot. Alul a kvantálási hiba vagy kerekítési zaj grafikonja látható, amelyet úgy számítunk ki, hogy a kvantált jelet kivonjuk a bemeneti jelből.

A kvantálási zaj a kerekítési hibák révén annál nagyobb, minél kisebb a bitmélység.
A bitmélység növelésével a kvantált jel egyértelműen jobban megfelel a bemeneti jelnek. Azonban nem ez a fontos, figyeljük meg a sokkal nagyobb hiba/zaj jelet az alacsonyabb bitmélységeknél. A kvantált jel nem távolított el adatokat a bemenetünkről, hanem valójában hozzáadta ezt a hibajelet. Az additív szintézis azt mondja, hogy egy jelet bármely két másik jel összegével lehet reprodukálni, beleértve a fázison kívüli jeleket is, amelyek kivonásként hatnak. Így működik a zajszűrés. Tehát ezek a kerekítési hibák egy új zajjelet vezetnek be.
Ez nem csak elméleti kérdés, valóban egyre több és több zajt lehet hallani az alacsonyabb bitmélységű hangfájlokban. Hogy megértsük, miért, vizsgáljuk meg, mi történik a 2 bites példában nagyon kis jelekkel, például 0,2 másodperc előtt. Kattintson ide a nagyított grafikonért. A bemeneti jel nagyon kis változásai nagy változásokat eredményeznek a kvantált változatban. Ez a kerekítési hiba működése, amelynek hatására a kisjelű zaj felerősödik. Tehát még egyszer: a zaj a bitmélység csökkenésével egyre hangosabbá válik.
A kvantálás nem távolít el adatokat a bemenetünkről, hanem valójában egy zajos hibajelet ad hozzá.
Gondoljuk ezt fordítva is: nem lehet a kvantálási lépés méreténél kisebb jelet rögzíteni – ironikusan a legkisebb szignifikáns bitnek nevezett jelet. A kis jelváltozásoknak a legközelebbi kvantálási szintre kell felugraniuk. A nagyobb bitmélységek kisebb kvantálási lépésekkel és így kisebb mértékű zajerősítéssel járnak.
A legfontosabb azonban, hogy a kvantálási zaj amplitúdója a bemeneti jelek amplitúdójától függetlenül állandó marad. Ez azt mutatja, hogy a zaj az összes különböző kvantálási szinten előfordul, tehát minden adott bitmélységnél következetes zajszint van. A nagyobb bitmélység kisebb zajt eredményez. Ezért a 16 és 24 bitmélység közötti különbségekre nem úgy kell gondolnunk, mint a hullámforma alakjának pontosságára, hanem mint a rendelkezésre álló határértékre, mielőtt a digitális zaj zavarja a jelünket.
A bitmélység a zajról szól
Most, hogy a bitmélységről a zaj szempontjából beszélünk, térjünk vissza még egyszer a fenti grafikánkhoz. Figyeljük meg, hogy a 8 bites példa szinte tökéletesen megfelel a zajos bemeneti jelünknek. Ez azért van így, mert a 8 bites felbontása valóban elegendő a háttérzaj szintjének megragadásához. Más szóval: a kvantálási lépésméret kisebb, mint a zaj amplitúdója, vagy a jel-zaj viszony (SNR) jobb, mint a háttérzaj szintje.
A 20log(2n) egyenlet, ahol n a bitmélység, megadja nekünk az SNR-t. Egy 8 bites jel SNR-je 48 dB, a 12 bitesé 72 dB, míg a 16 bites 96 dB, a 24 bites pedig 144 dB. Ez azért fontos, mert most már tudjuk, hogy csak olyan bitmélységre van szükségünk, amelynek SNR-je elegendő ahhoz, hogy a háttérzaj és a rögzíteni kívánt leghangosabb jel közötti dinamikatartományt befogadja, és a hangot olyan tökéletesen adja vissza, ahogy az a valóságban is megjelenik. Kicsit bonyolulttá válik a digitális világ relatív skáláiról a fizikai világ hangnyomás-alapú skáláira való áttérés, ezért megpróbáljuk egyszerűbbé tenni a dolgot.
Egy olyan bitmélységre van szükségünk, amelynek SNR-értéke elegendő a háttérzajunkhoz, hogy a hangunkat olyan tökéletesen rögzítsük, ahogy az a valós világban megjelenik.
A fülünk érzékenysége 0 dB (csend) és körülbelül 120 dB (fájdalmasan hangos hang) között mozog, és a hangerő megkülönböztetésének tipikus képessége mindössze 1 dB között van. Tehát a fül dinamikai tartománya körülbelül 120dB, vagyis közel 20 bit.
Azt azonban nem halljuk egyszerre, hogy mindezt egyszerre halljuk, mivel a dobhártya, vagyis a dobhártya összehúzódik, hogy hangos környezetben csökkentse a belső fülbe ténylegesen eljutó hangerő mennyiségét. Zenét sem fogsz közel sem ilyen hangosan hallgatni, mert megsüketülsz. Ráadásul az a környezet, amelyben Ön és én zenét hallgatunk, nem olyan csendes, mint amilyet az egészséges fül hall. Egy jól kezelt hangstúdióban talán 20 dB alá csökken a háttérzaj, de egy nyüzsgő nappaliban vagy a buszon való hallgatás nyilvánvalóan rontja a körülményeket, és csökkenti a nagy dinamikai tartomány iránti igényünket.
Az emberi fülnek hatalmas dinamikai tartománya van, csak éppen nem egyszerre az egész. A maszkolás és a hallásvédelem csökkenti a hatékonyságát.
Az egésznek a tetejébe: a hangerő növekedésével a fülben magasabb frekvenciájú maszkolás lép érvénybe. Alacsony, 20-40 dB-es hangerőn a maszkolás nem jelentkezik, kivéve a közeli hangmagasságú hangokat. Azonban 80dB-nél a 40dB alatti hangok elmaszkírozódnak, míg 100dB-nél a 70dB alatti hangokat lehetetlen meghallani. A fül és a hallott anyag dinamikus jellege miatt nehéz pontos számot mondani, de az Ön hallásának valódi dinamikai tartománya átlagos környezetben valószínűleg 70 dB körül van, nagyon hangos környezetben pedig mindössze 40 dB-ig terjed. A legtöbb embert valószínűleg már 12 bites bitmélység is kielégítené, így a 16 bites CD-k bőséges mozgásteret biztosítanak számunkra.

hiperfizika A nagyfrekvenciás maszkolás nagy hallgatási hangerőn jelentkezik, ami korlátozza a halkabb hangok érzékelését.
A legtöbb hangszer és felvételi mikrofon is zajjal jár (különösen a gitárerősítők), még a nagyon csendes hangstúdiókban is. A különböző műfajok dinamikatartományával kapcsolatban is készült néhány tanulmány, köztük ez, amely egy tipikus 60 dB-es dinamikatartományt mutat be. Nem meglepő, hogy a csendesebb részeket kedvelő műfajok, mint például a kórus, az opera és a zongora, 70 dB körüli maximális dinamikatartományt mutattak, míg a “hangosabb” rock, pop és rap műfajok inkább 60 dB és az alatti értékeket mutattak. Végső soron a zenét csak ennyi hűséggel lehet előállítani és rögzíteni.
A zeneipar “hangossági háborúi” is ismerősek lehetnek, ami minden bizonnyal meghiúsítja a mai Hi-Res audioformátumok célját. A tömörítés erőteljes használata (amely felerősíti a zajt és csillapítja a csúcsokat) csökkenti a dinamikai tartományt. A modern zenének lényegesen kisebb a dinamikatartománya, mint a 30 évvel ezelőtti albumoknak. Elméletileg a modern zenét alacsonyabb bitrátával lehetne terjeszteni, mint a régi zenét. Itt megnézheti számos album dinamikatartományát.

A CD minősége lehet, hogy “csak” 16 bites, de ez a minőség szempontjából túlzás.
16 bitre van szükség
Ez egy elég nagy utazás volt, de remélhetőleg sokkal árnyaltabb képet kaptál a bitmélységről, a zajról és a dinamikatartományról, mint azok a félrevezető lépcsőzetes példák, amelyeket oly gyakran látsz.
A bitmélység a zajról szól, és minél több bit adatot tárolsz az audióban: annál kevesebb kvantálási zaj kerül a felvételedbe. Ugyanígy a kisebb jeleket is pontosabban tudja rögzíteni, ami segít a digitális zajszintet a felvétel vagy a hallgatási környezet alá szorítani. Ennyire van szükségünk a bitmélységre. Nincs semmi előnye annak, ha hatalmas bitmélységű hangmestereket használunk.
Meglepő módon 12 bit valószínűleg elegendő egy tisztességes hangzású zenei masterhez és a legtöbb hallgatási környezet dinamikai tartományának kiszolgálásához. A digitális hang azonban nem csak zenét közvetít, és az olyan példák, mint a beszéd vagy a televíziós környezeti felvételek szélesebb dinamikatartományt használhatnak, mint a legtöbb zene. Ráadásul egy kis mozgástér a hangos és a halk hangok elkülönítésére senkinek sem árthat.
Összességében a 16 bit (96 dB dinamikatartomány vagy 120 dB dithering alkalmazásával) a hangtípusok széles skáláját, valamint az emberi hallás és a tipikus hallgatási környezetek határait is figyelembe veszi. A 24 bites minőség érzékelhető növekedése erősen vitatható, ha nem egyszerűen placebo, ahogy remélem, bebizonyítottam. Ráadásul a fájlméret és a sávszélesség növekedése szükségtelenné teszi őket. A zenei könyvtár vagy stream fájlméretének csökkentésére használt tömörítés típusa sokkal észrevehetőbb hatással van a hangminőségre, mint az, hogy 16 vagy 24 bites fájlról van-e szó.