
Először is próbáld meg megoldani ezeket, és magyarázd meg anélkül, hogy látnád a választ.
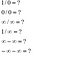
Ezek a kifejezések gyakran próbálnak összezavarni minket, mert a legtöbbünknek nincs meg a megfelelő megértése. Most nézd meg a válaszokat.

valami/0:
A válaszok láttán talán elgondolkodsz. Ha nem, akkor jó. A dolog lényege, hogy valami osztva 0-val mindig meghatározatlan, mert az értéket még nem definiálták. Tehát mikor mondjuk azt, hogy ez a valami osztva 0-val végtelen? Persze, ezeket már sokszor láttuk, de miért mondjuk ezt?
Nos, a valami osztva 0-val végtelen az egyetlen eset, amikor határértéket használunk. A végtelen nem egy szám, hanem egy szám hossza. Amikor határértéket használunk, mindig arra gondolunk, hogy x tendál valamihez, nem pedig arra, hogy x egyenlő valamivel. Ezért valójában nem tudjuk kitalálni a számot. Mivel nem tudjuk kitalálni a pontos számot, egy szám hosszának vagy végtelennek tekintjük. Normális esetben valaminek a 0-val osztott értéke még nincs meghatározva, tehát meghatározatlan.
Meghatározhatatlan alak:
0/0 és a végtelen osztva végtelennel határozatlan. Miért? Ebben az esetben a matematikai kifejezések helyesek. Kell lennie egy értéknek, de nem határoztuk meg a pontos értéket. Előfordulhat, hogy megvan az érték, de az is lehet, hogy meghatározatlan. Nem tudjuk. Ezért azt mondjuk, hogy ezek a kifejezések határozatlan alakban vannak.
Ugyanezen okból a végtelen mínusz végtelen és a (mínusz végtelen mínusz végtelen) is határozatlan alakban van, nem pedig nulla vagy mínusz végtelen, mert a végtelen lehet bármilyen pozitív vagy negatív szám. Tehát a mínusz végtelen mínusz végtelen nem fog mindig negatív irányba mozogni.
Egy másik hasonló kifejezés, amely a végtelen szorozva 0-val, követi ezt a szabályt. Ezért ez is határozatlan alakú.
1 osztva a végtelennel:
Ez esetben, ha egy kis számot elosztunk egy nagy számmal, az eredmény nagyon közel kerül a nullához. Ezért nullának tekintjük.
Példa: