MezopotámiaiSzerkesztés
A Kr. e. 2700-2300 közötti időszakban jelent meg először a sumér abakusz, egy egymást követő oszlopokból álló táblázat, amely a szekszagézimális számrendszerük egymást követő nagyságrendjeit határolta.
Egyes tudósok a babiloni ékírás egy olyan karakterére mutatnak rá, amely az abakusz ábrázolásából származhat. Olyan óbabiloni tudósok, mint Carruccio, úgy vélik, hogy az óbabiloniak “az összeadás és kivonás műveleteire használhatták az abakuszt; ez a kezdetleges eszköz azonban bonyolultabb számításokhoz nehezen használhatónak bizonyult”.
EgyiptomiSzerkesztés
Az abakusz használatát az ókori Egyiptomban Hérodotosz görög történetíró említi, aki azt írja, hogy az egyiptomiak jobbról balra manipulálták a kavicsokat, ellentétes irányban, mint a görög balról jobbra módszer. A régészek különböző méretű ősi korongokat találtak, amelyeket feltehetően számlálóként használtak. Ennek az eszköznek a fali ábrázolásait azonban nem fedezték fel.
PerzsaSzerkesztés
Az Achaemenida Birodalom idején, i. e. 600 körül a perzsák kezdték el először használni az abakuszt. A Pártus, a Szasszanida és az Iráni Birodalom alatt a tudósok a tudás és a találmányok cseréjére összpontosítottak a környező országokkal – Indiával, Kínával és a Római Birodalommal -, amikor a feltételezések szerint más országokba is exportálták.
GreekEdit
A görög abakusz használatának legkorábbi régészeti bizonyítékai a Kr. e. 5. századból származnak. Démoszthenész (Kr. e. 384-322) is beszélt arról, hogy a fejnek túl nehéz számításokhoz kavicsokat kellett használni. A Kr. e. 4. századból származó Alexis egyik színdarabja abakuszt és kavicsokat említ a számoláshoz, és Diogenész és Polübiosz is említést tesz olyan emberekről, akik néha többet, néha kevesebbet jelentettek, mint a kavicsok az abakuszon. A görög abakusz egy fából vagy márványból készült asztal volt, amelyet fából vagy fémből készült kis számlálókkal állítottak be a matematikai számításokhoz. Ezt a görög abakuszt használták az akhaemeniida Perzsiában, az etruszk civilizációban, az ókori Rómában és a francia forradalomig a nyugati keresztény világban.
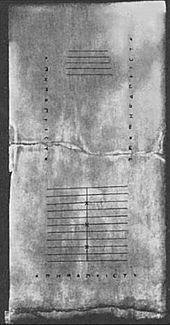
A görög Szalamisz szigetén Kr. u. 1846-ban talált tábla (a szalamiszi tábla) Kr. e. 300-ból származik, így ez a legrégebbi eddig felfedezett számolótábla. Ez egy 149 cm hosszú, 75 cm széles és 4,5 cm vastag fehér márványtábla, amelyen 5 jelcsoport található. A tábla közepén egy függőleges vonallal egyenlően osztott 5 párhuzamos vonalból álló csoport található, amelyet a legalsó vízszintes vonal és az egyetlen függőleges vonal metszéspontjában egy félkör zár le. E vonalak alatt egy széles tér található, amelyet egy vízszintes repedés választ el. E repedés alatt egy másik, tizenegy párhuzamos vonalból álló csoport található, amelyet ismét egy rájuk merőleges vonal oszt két részre, de a félkör a metszéspont tetején van; e vonalak közül a harmadik, a hatodik és a kilencedik vonal a függőleges vonallal való metszéspontjuknál kereszttel van jelölve. Szintén ebből az időszakból származik a Dareiosz-váza, amelyet 1851-ben tártak fel. Képek borították, köztük egy “kincstárnok”, aki egyik kezében viasztáblát tart, míg a másikkal egy asztalon lévő számlálót manipulál.
KínaiSzerkesztés

| Abakusz | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tradicionális kínai | 算盤 | |||||||||||||||
| Egyszerűsített kínai | 算盘 | |||||||||||||||
| Lit. jelentése | “számoló tálca” | |||||||||||||||
| Átírás | Standard mandarin | Hanyu Pinyin | IPA | Yue: Kantoni | Yale Romanizáció | Jyutping | IPA | Déli Min | Hokkien POJ | Tâi-lô | ||||||
A kínai abakusz legkorábbi ismert írásos dokumentációja a Kr. e. 2. századból származik.
A kínai abakusz, amelyet suanpan (算盤/算盘, szó szerint “számolótálca”) néven ismernek, jellemzően 20 cm (8 in) magas és a kezelőtől függően különböző szélességű. Általában több mint hét rúddal rendelkezik. A felső fedélzeten minden rúdon két gyöngy található, az alsó fedélzeten pedig egyenként öt gyöngy. A gyöngyök általában lekerekítettek és keményfából készülnek. A gyöngyöket úgy számolják, hogy a gerenda felé felfelé vagy lefelé mozgatják őket; a gerenda felé mozgatott gyöngyöket számolják, míg a gerendától távolodókat nem. A felső gyöngyök egyike 5, míg az alsó gyöngyök egyike 1. Minden rúd alatt egy szám van, amely a helyértéket mutatja.A suanpan azonnal visszaállítható a kiindulási helyzetbe, ha a vízszintes tengely mentén egy gyors mozdulattal az összes gyöngyöt elfordítjuk a középen lévő vízszintes gerendától.
A kínai abakusz prototípusa a Han-dinasztia idején jelent meg, és a gyöngyök oválisak. A Song-dinasztia és korábban az 1:4 típusú vagy négygyöngyös abakuszt használták, amely hasonló a modern abakuszhoz, beleértve a gyöngyök alakját is, amelyet általában japán stílusú abakuszként ismernek.
A Ming-dinasztia elején az abakusz 1:5 abakusz formájában kezdett megjelenni. A felső fedélzet egy, az alsó pedig öt gyöngyöt tartalmazott.
A késői Ming-dinasztia idején az abakuszstílusok 2:5 formában jelentek meg. A felső pakliban két gyöngy volt, az alsóban pedig öt gyöngy.
A Suanpan számára különböző számítási technikákat dolgoztak ki, amelyek lehetővé tették a hatékony számításokat. Jelenleg is léteznek olyan iskolák, ahol a diákokat tanítják a használatára.
A Song-dinasztia idején (960-1297) Zhang Zeduan által festett hosszú tekercsen A folyó mentén a Qingming-fesztivál idején egy patika (Feibao) pultján egy számlakönyv és orvosi receptek mellett jól látható egy suanpan.
A római abakusz és a kínai abakusz hasonlósága arra utal, hogy az egyik inspirálhatta a másikat, mivel van némi bizonyíték a Római Birodalom és Kína közötti kereskedelmi kapcsolatra. Közvetlen kapcsolat azonban nem mutatható ki, és az abakuszok hasonlósága lehet véletlenszerű, mindkettő végső soron a kézenkénti öt ujjal való számolásból ered. Míg a római modell (mint a legtöbb modern koreai és japán) tizedesjegyenként 4 plusz 1 gyöngyöt tartalmaz, addig a standard suanpan 5 plusz 2 gyöngyöt. Ez egyébként lehetővé teszi a hexadecimális számrendszer (vagy bármelyik bázis 18-ig) használatát, amelyet a hagyományos kínai súlyméréseknél használhattak. (Ahelyett, hogy drótokon futnának, mint a kínai, koreai és japán modellekben, a római modell gyöngyei barázdákban futnak, ami feltehetően sokkal lassabbá teszi a számtani számításokat.
A suanpan másik lehetséges forrása a kínai számolórudak, amelyek tizedes rendszerrel működtek, de hiányzott a nulla mint helyőrző fogalma. A nulla valószínűleg a Tang-dinasztia (618-907) idején került a kínaiakhoz, amikor az Indiai-óceánon és a Közel-Keleten tett utazások közvetlen kapcsolatot biztosíthattak Indiával, így az indiai kereskedőktől és matematikusoktól elsajátíthatták a nulla és a tizedesjegy fogalmát.
RomanEdit

A számolás szokásos módszere az ókori Rómában, akárcsak Görögországban, a számlálók mozgatása volt egy sima asztalon. Eredetileg kavicsokat (calculi) használtak. Később és a középkori Európában jetont gyártottak. A római számrendszerhez hasonlóan jelzett vonalak jelezték az egységeket, ötösöket, tízeseket stb. A “számlálóöntés” rendszere a késő római birodalomban és a középkori Európában is fennmaradt, és korlátozottan még a XIX. században is használták. Az abakusz II. Szilveszter pápa által módosított formában történő újbóli bevezetésének köszönhetően a 11. században ismét széles körben elterjedt Európában. Ez az abakusz a hagyományos római számolótáblákkal ellentétben drótokra fűzött gyöngyöket használt, ami azt jelentette, hogy az abakuszt sokkal gyorsabban lehetett használni.
Horatius az i. e. 1. században írva utal a viasz abakuszra, egy vékony fekete viaszréteggel borított táblára, amelyre ceruzával oszlopokat és számokat írtak.
A római abakusz egyik régészeti bizonyítéka, amely itt rekonstrukcióban látható, a Kr. u. 1. századból származik. Nyolc hosszú barázdája van, amelyekben egyenként legfeljebb öt gyöngyöt tartalmaz, és nyolc rövidebb barázdája, amelyekben egy vagy egy gyöngy sincs. Az I jelű barázda az egységeket, az X a tízeseket, és így tovább a milliókig. A rövidebb barázdákban lévő gyöngyök öt-öt egységet, öt tízest stb. jelölnek, lényegében a római számokkal rokon, kétnégyes kódolású tizedes rendszerben. A jobb oldali rövid barázdákat a római “unciák” (azaz a törtek) jelölésére használhatták.
IndianEdit
Vasubandhu (316-396) Abhidharmakośabhāṣya című szanszkrit nyelvű műve a buddhista filozófiáról, szerint a Kr. u. II. századi filozófus, Vasumitra azt mondta, hogy “egy kanócot (szanszkrit vartikā) az egyes számra (ekāṅka) helyezve azt jelenti, hogy egy, míg a kanócot a százas számra helyezve azt jelenti, hogy száznak nevezik, az ezres számra helyezve pedig azt, hogy ezer”. Nem világos, hogy pontosan mi lehetett ez az elrendezés. Az 5. század körül az indiai írnokok már új módszereket találtak az abakusz tartalmának rögzítésére. A hindu szövegek a śūnya (nulla) kifejezést használták az abakusz üres oszlopának jelölésére.
JapánSzerkesztés

A japánban az abakuszt sorobannak (算盤, そろばん, szó szerint “számolótálca”) nevezik, amelyet a 14. században importáltak Kínából. Valószínűleg a munkásosztály használta egy vagy több évszázaddal az uralkodó osztály megjelenése előtt, mivel az osztályszerkezet nem tette lehetővé, hogy az alsóbb osztály által használt eszközöket az uralkodó osztály átvegye vagy használja. Az 1/4-es abakusz, amely a ritkán használt második és ötödik gyöngyöt eltávolítja, az 1940-es években vált népszerűvé.
A mai japán abakusz 1:4-es típusú, négy gyöngyös abakusz Kínából került be a Muromachi korszakban. A felső fedélzet egy gyöngy és az alsó négy gyöngy formáját veszi át. A felső gyöngy a felső fedélzeten egyenlő volt öt, az alsó pedig egyenlő egy, mint a kínai vagy koreai abakusz, és a tizedes szám kifejezhető, így az abakuszt egy négy abakuszként tervezték. A gyöngyök mindig gyémánt alakúak. A hányados osztást általában az osztási módszer helyett használják; ugyanakkor annak érdekében, hogy a szorzás és az osztás számjegyei következetesen használják az osztási szorzást. Később Japánban volt egy 3:5 arányú abakusz, a 天三算盤, amely ma a Yamagata város Shansi falujának Ize Rongji gyűjteménye. Voltak 2:5 típusú abakuszok is.
A négygyöngyös abakusz elterjedésével a japán abakuszok használata is elterjedt világszerte. Különböző helyeken továbbfejlesztett japán abakuszok is vannak. Az egyik Kínában gyártott japán abakusz egy alumíniumkeretes műanyag gyöngyös abakusz. A fájl a négy gyöngy mellett van, és az “elszámolási” gomb, nyomja meg az elszámolási gombot, azonnal a felső gyöngyöt a felső pozícióba helyezi, az alsó gyöngyöt az alsó pozícióba tárcsázza, azonnal elszámol, könnyen használható.
Az abakuszt ma is Japánban gyártják, még a zsebszámológépek elterjedésével, praktikumával és megfizethetőségével együtt is. A soroban használatát még mindig tanítják a japán általános iskolákban a matematika részeként, elsősorban a gyorsabb szellemi számolás segédeszközeként. A soroban vizuális megjelenítésével ugyanolyan idő alatt, vagy még gyorsabban juthatunk el a válaszhoz, mint egy fizikai eszközzel.
KoreanEdit
A kínai abakusz i.sz. 1400 körül vándorolt Kínából Koreába. A koreaiak jupan (주판), supan (수판) vagy jusan (주산) néven emlegetik.A négy gyöngyös abakuszt( 1:4 ) a Song-dinasztia idején Kínából a Goryeo-dinasztia, később az öt gyöngyös abakuszt (5:1) a Ming-dinasztia idején Kínából a koreaiakhoz került.
Native AmericanEdit


Egyes források említik a nepohualtzintzin nevű abakusz használatát az ősi azték kultúrában. Ez a mezoamerikai abakusz egy 5 számjegyű 20-as bázisú rendszert használt. a Nepōhualtzintzin szó a nahuatl nyelvből származik, és a következő gyökökből képződik; Ne – személyes -; pōhual vagy pōhualli – a számla -; és tzintzin – kis hasonló elemek. Teljes jelentését így vették át: kis hasonló elemekkel való számolás valaki által. Használatát a Calmecacban tanították a temalpouhqueh , akik az égiek számonkérésére szentelt tanulók voltak, gyermekkoruktól kezdve.
A Nepōhualtzintzin két fő részre volt osztva, amelyeket egy sáv vagy köztes zsinór választott el egymástól. A bal oldali részben négy gyöngy volt, amelyek az első sorban egységnyi értékkel rendelkeztek (1, 2, 3 és 4), a jobb oldalon pedig három gyöngy, amelyek értéke 5, 10 és 15 volt. Ahhoz, hogy megismerjük a felső sorok megfelelő gyöngyeinek értékét, elég, ha megszorozzuk 20-cal (minden soronként) az első sorban lévő megfelelő számla értékét.
Ez összesen 13 sor volt, mindegyikben 7 gyönggyel, ami 91 gyöngyöt tett ki minden egyes Nepōhualtzintzinben. Ez egy alapvető szám volt, hogy megértsük, 7-szer 13, a természeti jelenségek, az alvilág és az égbolt ciklusai között felfogott szoros kapcsolatot. Egy Nepōhualtzintzin (91) az év egy évszakának napjainak számát jelentette, két Nepōhualtzintzin (182) a kukorica ciklusának napjainak száma a vetéstől az aratásig, három Nepōhualtzintzin (273) a csecsemő várandósságának napjainak száma, négy Nepōhualtzintzin (364) pedig egy ciklust fejezett be és megközelítőleg egy évet jelentett (11/4 nap híján). A modern számítógépes aritmetikára lefordítva a Nepōhualtzintzin a 10-től a 18-ig terjedő rangot jelentette lebegőpontban, amely abszolút pontossággal számította ki a csillag-, valamint a végtelen mennyiségeket, ami azt jelentette, hogy nem volt megengedett a kerekítés.
A Nepōhualtzintzin újrafelfedezése David Esparza Hidalgo mexikói mérnöknek köszönhető, aki Mexikó-szerte tett vándorlásai során különféle metszeteket és festményeket talált erről a műszerről, és több példányt rekonstruált aranyból, jádéból, kagylóberakásokból stb. készült. Találtak még nagyon régi, az olmec kultúrának tulajdonított Nepōhualtzintzint, sőt néhány maja eredetű karkötőt is, valamint más kultúrákban is sokféle formát és anyagot.
George I. Sanchez, “Arithmetic in Maya”, Austin-Texas, 1961, talált egy másik 5 bázisú, 4 bázisú abakuszt a Yucatán-félszigeten, amely naptári adatokat is számolt. Ez egy ujjas abakusz volt, az egyik kezén 0, 1, 2, 3 és 4; a másik kezén pedig 0, 1, 2 és 3 volt. Figyeljük meg a nulla használatát a két ciklus elején és végén. Sanchez együtt dolgozott Sylvanus Morley-val, egy neves maja tudóssal.
Az inkák quipu egy színes, csomózott zsinórokból álló rendszer volt, amelyet számadatok rögzítésére használtak, mint a fejlett számolóbotokat – de nem számítások elvégzésére. A számításokat egy yupana (quechua nyelven “számolóeszköz”; lásd az ábrát) segítségével végezték, amelyet Peru meghódítása után is használtak. A yupana működési elve ismeretlen, de 2001-ben Nicolino De Pasquale olasz matematikus magyarázatot adott ezen eszközök matematikai alapjaira. Több yupana formájának összehasonlításával a kutatók megállapították, hogy a számítások alapja a Fibonacci-sorozat 1, 1, 2, 3, 5, valamint 10, 20 és 40 hatványai voltak, mint a hangszer különböző mezőinek helyértékei. A Fibonacci-sorozat használata minimálisra csökkentette az egy mezőn belüli szemek számát.
RussianEdit

Az orosz abakusz, a szoty (oroszul: счёты, többes szám az oroszból: счёт, számolás), általában egyetlen ferde fedélzettel rendelkezik, minden huzalon tíz gyöngyöt tartalmaz (kivéve egy, általában a felhasználó közelében elhelyezett huzalt, amelyen négy gyöngy található a negyedrubeles törtek számára). A régebbi modelleken van még egy 4 gyöngyös huzal a negyed-kopekek számára, amelyeket 1916-ig vertek. Az orosz abakuszt gyakran függőlegesen használják, az egyes huzalok balról jobbra haladnak, mint egy könyvben a sorok. A huzalokat általában úgy hajlítják meg, hogy középen felfelé domborodjanak, hogy a gyöngyöket a két oldal valamelyikére tűzzék. Akkor tisztul, amikor az összes gyöngyöt jobbra mozgatják. A manipuláció során a gyöngyök balra mozognak. A könnyebb áttekinthetőség érdekében a középső 2 gyöngy minden dróton (az 5. és 6. gyöngy) általában más színű, mint a másik nyolc gyöngy. Hasonlóképpen az ezres drót bal oldali gyöngye (és a milliós drót, ha van) is lehet más színű.
Az orosz abakusz egyszerű, olcsó és megbízható eszközként az egész volt Szovjetunióban minden üzletben és piacon használatos volt, és a használatát a legtöbb iskolában egészen az 1990-es évekig tanították. Még az 1874-ben feltalált mechanikus számológép, az Odhner aritmométer sem váltotta fel őket Oroszországban; Jakov Perelman szerint még az ő idejében is előfordult, hogy néhány üzletember, aki megpróbált ilyen eszközöket importálni az Orosz Birodalomba, kétségbeesetten feladta és távozott, miután megmutatták neki egy képzett abakuszkezelő munkáját. Hasonlóképpen a Felix aritmométerek 1924 óta tartó tömeges gyártása sem csökkentette jelentősen használatukat a Szovjetunióban. Az orosz abakusz csak azután kezdte elveszíteni népszerűségét, hogy a Szovjetunióban 1974-ben megkezdődött a mikroszámológépek tömeggyártása. Ma már archaizmusnak tekintik, és felváltotta a kézi számológép.
Az orosz abakuszt 1820 körül Jean-Victor Poncelet matematikus hozta Franciaországba, aki Napóleon hadseregében szolgált és oroszországi hadifogságban volt. Az abakusz a 16. században kikerült a használatból Nyugat-Európában a tizedesjegyrendszer és az algoritmikus módszerek elterjedésével. Poncelet francia kortársai számára ez valami újat jelentett. Poncelet nem alkalmazott célokra, hanem tanítási és demonstrációs segédeszközként használta. A törökök és az örmények is használtak az orosz schotyhoz hasonló abakuszt. A törökök coulba-nak, az örmények pedig chorebnek nevezték el.