A standard eltérés az adathalmaz átlagos változékonysága. Megmutatja, hogy az egyes értékek átlagosan milyen messze vannak az átlagtól.
A magas szórás azt jelenti, hogy az értékek általában messze vannak az átlagtól, míg az alacsony szórás azt jelzi, hogy az értékek az átlaghoz közel csoportosulnak.
Miről árulkodik a szórás?
A szórás a normál eloszlások szórásának hasznos mérőszáma.
A normál eloszlásokban az adatok szimmetrikus eloszlásúak, ferdeség nélkül. A legtöbb érték egy központi régió köré csoportosul, és az értékek a középponttól távolodva csökkenek. A szórás megmondja, hogy az adatok átlagosan mennyire szóródnak el az eloszlás középpontjától.
Sok tudományos változó követ normális eloszlást, például a magasság, a szabványosított teszteredmények vagy a munkahelyi elégedettségi értékelések. Ha megvan a különböző minták szórásai, akkor statisztikai tesztek segítségével összehasonlíthatja eloszlásaikat, hogy következtetéseket vonhasson le a nagyobb populációkra vonatkozóan, amelyekből származnak.
Az értékelések átlaga (M) minden csoport esetében azonos – ez az x-tengelyen az az érték, amikor a görbe a csúcspontján van. Standardeltéréseik (SD) azonban eltérnek egymástól.
A standard eltérés az eloszlás szórását tükrözi. A legkisebb szórással rendelkező görbe magas csúccsal és kis szórással rendelkezik, míg a legnagyobb szórással rendelkező görbe laposabb és szélesebb körű.
Az empirikus szabály
A szórás és az átlag együttesen meg tudja mondani, hogy hol található az eloszlásban a legtöbb érték, ha az normális eloszlást követ.
Az empirikus szabály, vagy a 68-95-99,7 szabály megmondja, hogy hol helyezkednek el az értékeid:
- A pontszámok 68%-a az átlag 2 szórásán belül van,
- A pontszámok 95%-a az átlag 4 szórásán belül van,
- A pontszámok 99.A pontszámok 7%-a az átlag 6 szórásán belül van.
Az empirikus szabály szerint:
- A pontszámok mintegy 68%-a 40 és 60 között van.
- A pontszámok mintegy 95%-a 30 és 70 között van.
- A pontszámok 99,7%-a 20 és 80 között van.
Az empirikus szabály egy gyors módja annak, hogy áttekintést kapjon az adatokról, és ellenőrizze, hogy nincsenek-e kiugró vagy szélsőséges értékek, amelyek nem ezt a mintát követik.
A nem normális eloszlások esetében a szórás kevésbé megbízható mérőszáma a változékonyságnak, és más mérőszámokkal, például a tartomány vagy az interkvartilis tartomány kombinálva kell használni.
Szabványeltérési képletek populációk és minták esetében
A szórás kiszámítására különböző képleteket használnak attól függően, hogy teljes populációból vagy mintából származó adatokról van szó.
Populációs szórás
Ha a téged érdeklő populáció minden tagjától gyűjtöttél adatokat, akkor a populációs szórás pontos értékét megkaphatod.
A populációs szórás képlete így néz ki:
| Formula | Magyarázat |
|---|---|
 |
|
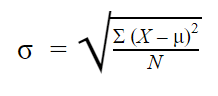Minta szórás
Ha mintából gyűjtünk adatokat, a minta szórásából becsléseket vagy következtetéseket vonhatunk le a populáció szórására vonatkozóan.
A minta szórásképlete így néz ki:
| Formula | Magyarázat |
|---|---|
 |
|
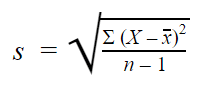Minták esetén a képletben n – 1-et használunk, mert n használatával torzított becslést kapnánk, amely következetesen alábecsüli a változékonyságot. A minta szórása általában alacsonyabb lenne, mint a sokaság valós szórása.
A minta n-nek n – 1-re való csökkentése mesterségesen nagyra növeli a szórást, így konzervatív becslést ad a változékonyságra.
Bár ez nem egy torzítatlan becslés, mégis kevésbé torzított becslése a szórásnak: jobb inkább túlbecsülni, mint alábecsülni a minták variabilitását.
A szórás kiszámításának lépései
A szórást általában automatikusan kiszámítja az a szoftver, amelyet a statisztikai elemzéshez használ. De kézzel is kiszámíthatod, hogy jobban megértsd, hogyan működik a képlet.
A szórás kézzel történő meghatározásának hat fő lépése van. Egy 6 pontszámból álló kis adathalmazon keresztül fogjuk végigjárni a lépéseket.
| Adatkészlet | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
1. lépés: Az átlag megkeresése
Az átlag megkereséséhez adjuk össze az összes pontszámot, majd osszuk el a pontszámok számával.
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50
2. lépés: Keressük meg az egyes pontszámok átlagtól való eltérését
Vonjuk ki az átlagot az egyes pontszámokból, hogy megkapjuk az átlagtól való eltéréseket.
Mivel x̅ = 50, itt minden pontszámból kivonunk 50-et.
| Pontozás | Az átlagtól való eltérés |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
3. lépés: Négyzeteljük az átlagtól való minden egyes eltérést
Sokszorozzuk meg az átlagtól való minden egyes eltérést önmagával. Ez pozitív számokat fog eredményezni.
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81
4. lépés: Keressük meg a négyzetek összegét
Adjuk össze az összes eltérés négyzetét. Ezt nevezzük négyzetek összegének.
16 + 361 + 324 + 100 + 4 + 81 = 886
5. lépés: Keressük meg a szórást
A négyzetek összegét osztjuk el n – 1-gyel (minta esetén) vagy N-nel (sokaság esetén) – ez a szórás.
Mivel 6-os mintával dolgozunk, n – 1-t fogunk használni, ahol n = 6.
886 ÷ (6 – 1) = 886 ÷ 5 = 177.2
6. lépés: A szórás négyzetgyökének megkeresése
A szórás négyzetgyökének megkereséséhez a szórás négyzetgyökét vesszük.
√177,2 = 13,31
Azt tanulva, hogy SD = 13.31, azt mondhatjuk, hogy minden egyes pontszám átlagosan 13,31 ponttal tér el az átlagtól.
Miért hasznos a szórás a variabilitás mérésére?
Bár vannak egyszerűbb módszerek a variabilitás kiszámítására, a szórásképlet az egyenlőtlenül eloszló mintákat jobban súlyozza, mint az egyenletesen eloszló mintákat. A magasabb szórás azt mutatja, hogy az eloszlás nemcsak jobban eloszlik, hanem egyenetlenebbül is eloszlik.
Ez azt jelenti, hogy jobb képet ad az adatok változékonyságáról, mint az egyszerűbb mérőszámok, például az átlagos abszolút eltérés (MAD).
A MAD hasonló a szóráshoz, de könnyebben kiszámítható. Először is, az átlagtól való minden egyes eltérést abszolút értékekben fejezzük ki úgy, hogy pozitív számokká alakítjuk őket (például a -3-ból 3 lesz). Ezután kiszámítja ezeknek az abszolút eltéréseknek az átlagát.
A standard eltéréssel ellentétben a MAD esetében nem kell számok négyzetgyökeit vagy négyzetgyökeit kiszámítania. Emiatt azonban kevésbé pontos mérőszámot ad a változékonyságról.
Vegyünk két mintát, amelyeknek azonos a központi tendenciája, de különböző mértékű a változékonysága. A B minta változékonyabb, mint az A minta.
| értékek | közepes | közepes abszolút eltérés | standardeltérés | |
|---|---|---|---|---|
| A minta A | 66, 30, 40, 64 | 50 | 15 | 17.8 |
| B minta | 51, 21, 79, 49 | 50 | 15 | 23.7 |
Az átlagtól egyenlő átlagos eltérésű minták esetében a MAD nem képes különbséget tenni a szórás szintjei között. A szórás pontosabb: az átlagtól való eltérések nagyobb változatosságával rendelkező minták esetében magasabb.
Az átlagtól való eltérések négyzetre emelésével a szórás pontosabban tükrözi az egyenetlen szórást. Ez a lépés a szélsőséges eltéréseket jobban súlyozza, mint a kis eltéréseket.
Ez azonban érzékennyé teszi a szórást a kiugró értékekre is.
Gyakori kérdések a szórásról
A változékonyságot leggyakrabban a következő leíró statisztikákkal mérik:
- Tartomány: a legmagasabb és a legalacsonyabb érték közötti különbség
- Interkvartilis tartomány: Az eloszlás középső felének tartománya
- Szórás: az átlagtól való átlagos távolság
- Szórás: az átlagtól való távolságok négyzetének átlaga
A szórás az adathalmazodban lévő átlagos variabilitás mértéke. Megmutatja, hogy az egyes értékek átlagosan milyen messze vannak az átlagtól.
A normális eloszlásokban a magas szórás azt jelenti, hogy az értékek általában messze vannak az átlagtól, míg az alacsony szórás azt jelzi, hogy az értékek az átlaghoz közel csoportosulnak.
A normális eloszlásban az adatok szimmetrikusan, ferdeség nélkül oszlanak el. A legtöbb érték egy központi régió körül csoportosul, és az értékek a középponttól távolodva csökkennek.
A központi tendencia mértékegységei (átlag, módusz és medián) pontosan megegyeznek a normális eloszlásban.
Az empirikus szabály vagy a 68-95-99,7 szabály megmondja, hogy egy normális eloszlásban hol található a legtöbb érték:
- Az értékek körülbelül 68%-a az átlag 1 szórásán belül van.
- Az értékek körülbelül 95%-a az átlag 2 szórásán belül van.
- Az értékek körülbelül 99.Az értékek 7%-a az átlag 3 szórásán belül van.
Az empirikus szabály egy gyors módja annak, hogy áttekintést kapjon az adatokról, és ellenőrizze a kiugró vagy szélsőséges értékeket, amelyek nem követik ezt a mintát.
A variancia az átlagtól való átlagos négyzetes eltérés, míg a szórás ennek a számnak a négyzetgyöke. Mindkét mérték egy eloszlás változékonyságát tükrözi, de a mértékegységeik különböznek:
- A szórás az eredeti értékekkel megegyező mértékegységekben (pl. percekben vagy méterekben) van kifejezve.
- A szórás sokkal nagyobb mértékegységekben (pl. méter négyzetben) van kifejezve.
Bár a szórás mértékegységeit intuitív módon nehezebb megérteni, a szórás fontos a statisztikai tesztekben.