A műhold egy olyan test, amely egy másik test körül egy matematikailag kiszámítható pályán, az úgynevezett pályán mozog. A kommunikációs műhold nem más, mint egy mikrohullámú átjátszóállomás az űrben, amely a távközlés, a rádiózás és a televíziózás, valamint az internetes alkalmazások terén nyújt segítséget.
Az átjátszó egy olyan áramkör, amely megnöveli a fogadott jel erősségét és továbbítja azt. De itt ez az átjátszó transzponderként működik, amely megváltoztatja a sugárzott jel frekvenciasávját a fogadottól.
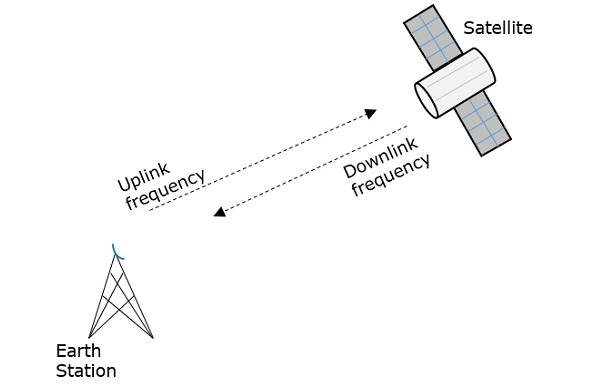
A frekvenciát, amellyel a jelet az űrbe küldik, Uplink frekvenciának nevezzük, míg a frekvenciát, amellyel a transzponder küldi, Downlink frekvenciának.
A következő ábra jól szemlélteti ezt a fogalmat.
Most nézzük meg a műholdas kommunikáció előnyeit, hátrányait és alkalmazásait.
Szatellitkommunikáció – Előnyök
A műholdas kommunikációnak számos előnye van, mint például –
-
Flexibilitás
-
Új áramkörök könnyű telepítése
-
A távolságok könnyen lefedhetők és a költségek nem számítanak
-
Sugárzás. lehetőségek
-
A Föld minden egyes szegletét lefedik
-
A felhasználó irányíthatja a hálózatot
Műholdas kommunikáció – Hátrányok
A műholdas kommunikációnak a következő hátrányai vannak –
-
A kezdeti költségek, például a szegmens- és indítási költségek túl magasak.
-
Frekvenciák túlterheltsége
-
Zavarás és terjedés
Szatellitkommunikáció – Alkalmazások
A műholdas kommunikáció a következő területeken talál alkalmazást –
-
A rádióközvetítésben.
-
A televíziós műsorszórásban, mint például a DTH.
-
Az internetes alkalmazásokban, mint például internetkapcsolat biztosítása adatátvitelhez, GPS-alkalmazások, internetes szörfözés stb.
-
A hangkommunikációban.
-
A kutatási és fejlesztési ágazatban, számos területen.
-
A katonai alkalmazásokban és navigációban.
A műhold pályáján való tájékozódás a Kepler-törvényeknek nevezett három törvénytől függ.
Kepler-törvények
Johannes Kepler (1571-1630) csillagász tudós 3 forradalmi törvényt adott a műholdak mozgására vonatkozóan. A pálya, amelyet egy műhold az elsődleges pontja (a Föld) körül követ, egy ellipszis. Az ellipszisnek két gyújtópontja van: F1 és F2, amelyek közül az egyik a Föld.
Ha az objektum középpontja és az ellipszis pályájának egy pontja közötti távolságot vesszük figyelembe, akkor az ellipszis középponttól legtávolabbi pontját apogeumnak, az ellipszis középponttól legrövidebb pontját pedig perigeumnak nevezzük.
Kepler 1. törvénye
Kepler 1. törvénye kimondja, hogy “minden bolygó elliptikus pályán kering a Nap körül, amelynek egyik fókuszpontja a Nap”. Ennek megfelelően egy műhold ellipszis alakú pályán mozog, amelynek egyik gyújtópontja a Föld.
Az ellipszis félnagy tengelyét “a”-val, a félkisebb tengelyét pedig b-vel jelöljük. Ezért e rendszer e excentricitása a következőképpen írható fel: –
$$e = \frac{\sqrt{a^{2}-b^{2}}}{a}}$$
-
Excentricitás (e) – Ez az a paraméter, amely meghatározza az ellipszis alakjának különbségét a kör alakjához képest.
-
Féltengely (a) – A két fókuszt a középpont mentén összekötő, a két apogeát (az ellipszis középponttól legtávolabbi pontjait) egyaránt érintő leghosszabb, a középpont mentén húzott átmérő.
-
Félkisebb tengely (b) – A középponton keresztül húzott legrövidebb átmérő, amely érinti mindkét perigeumot (az ellipszis középponttól legtávolabbi pontjait).
Az alábbi ábra jól mutatja ezeket.
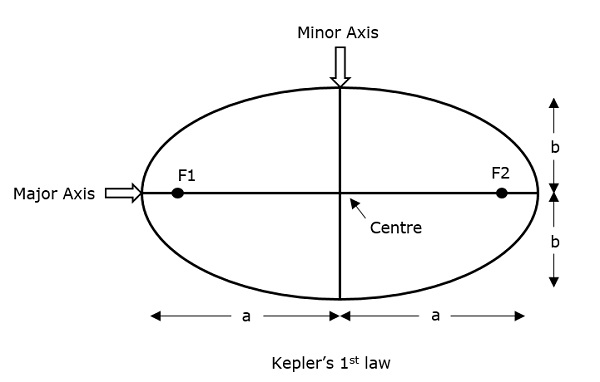
Elliptikus pálya esetén mindig kívánatos, hogy az excentricitás 0 és 1 között legyen, azaz.azaz 0 < e < 1, mert ha e nulla lesz, akkor a pálya már nem lesz ellipszis alakú, inkább körpályává alakul át.
Kepler 2. törvénye
Kepler 2. törvénye kimondja, hogy: “Azonos időintervallumok esetén a műhold által bejárt terület egyenlő a Föld középpontjához képest.”
Ezt a következő ábra segítségével érthetjük meg.”
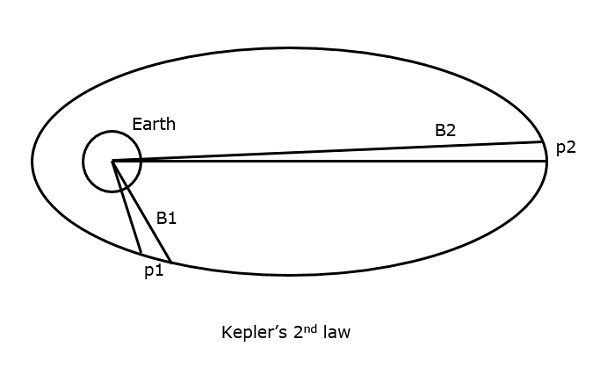
Tegyük fel, hogy a műhold p1 és p2 távolságot tesz meg, ugyanabban az időintervallumban, akkor a két esetben a B1 és B2 terület, amelyet a két esetre vonatkoztatva megtesz, egyenlő.
Kepler 3. törvénye
Kepler 3. törvénye kimondja, hogy: “A pálya periodikus idejének négyzete arányos a két test közötti átlagos távolság kockájával.”
Ez matematikailag így írható fel:
$$T^{2}\:\alpha\:\:a^{3}$$
Amiből következik
$$$T^{2} = \frac{4\pi ^{2}}{GM}a^{3}$$$
Ahol $\frac{4\pi ^{2}}{GM}$ az arányossági konstans (a newtoni mechanika szerint)
$$$T^{2} = \frac{4\pi ^{2}}{\mu}a^{3} $$
Hol μ = a Föld geocentrikus gravitációs állandója, i.azaz Μ = 3.986005 × 1014 m3/sec2
$$1 = \left ( \frac{2\pi}{T} \right )^{2}\frac{a^{3}}{\mu}$$
$$1 = n^{2}\frac{a^{3}}{\mu}\:\:\:\:\Rightarrow \:\:\:\:a^{3} = \frac{\mu}{n^{2}}$$
Ahol n = a műhold átlagos mozgása radián/másodpercben
A műholdak pályaműködését e Kepler-törvények segítségével számítják ki.
Ezek mellett van még egy fontos dolog, amit meg kell jegyezni. Egy műhold, amikor a Föld körül kering, a Földtől származó húzóerőnek van kitéve, ami a gravitációs erő. Emellett a Nap és a Hold részéről is érez némi húzóerőt. Ezért két erő hat rá. Ezek a következők: –
-
centripetális erő – Azt az erőt, amely egy pályán mozgó tárgyat hajlamos maga felé húzni, centripetális erőnek nevezzük.
-
centrifugális erő – Azt az erőt, amely egy pályán mozgó tárgyat hajlamos eltolni a helyétől, centrifugális erőnek nevezzük.
A műholdnak tehát ezt a két erőt kell egyensúlyban tartania, hogy pályáján maradjon.
Föld körüli pályák
A műholdat, amikor az űrbe indítják, egy bizonyos pályára kell állítani, hogy egy bizonyos utat biztosítson a forgásához, hogy megőrizze elérhetőségét és szolgálja a célját, legyen az tudományos, katonai vagy kereskedelmi. Az ilyen pályákat, amelyeket a műholdaknak a Földhöz képest kijelöltek, Föld körüli pályáknak nevezzük. Az ilyen pályán keringő műholdak Föld körüli pályán keringő műholdak.
A Föld körüli pályák fontos fajtái: –
-
Geoszinkron Föld körüli pálya
-
közepes Föld körüli pálya
-
alacsony Föld körüli pálya
Geoszinkron Föld körüli pályájú műholdak
A Geo-GEO (Geoszinkron Föld körüli pálya) műhold egy olyan műhold, amely 22 magasságban helyezkedik el,300 mérföldes magasságban van a Föld felett. Ez a pálya egy oldalsó valós nappal (azaz 23 óra 56 perccel) van szinkronizálva. Ez a pálya lehet dőlésszögű és excentricitású. Nem biztos, hogy kör alakú. Ez a pálya a Föld pólusainál megdőlhet. A Földről nézve azonban állónak tűnik.
Azt a geoszinkron pályát, amely kör alakú és az Egyenlítő síkjában van, geostacionárius pályának nevezzük. Ezek a műholdak a Föld Egyenlítője fölött 35 900 km magasságban helyezkednek el (ugyanúgy, mint a geoszinkron), és a Föld irányához képest (nyugat-kelet felé) folyamatosan forognak. Ezek a műholdak a Földhöz képest helyhez kötöttnek tekintendők, ezért a nevük is erre utal.
A geostacionárius Föld körüli pályán keringő műholdakat időjárás-előrejelzésre, műholdas TV, műholdas rádió és más típusú globális kommunikációra használják.
A következő ábra mutatja a geoszinkron és a geostacionárius pálya közötti különbséget. A forgástengely a Föld mozgását jelzi.
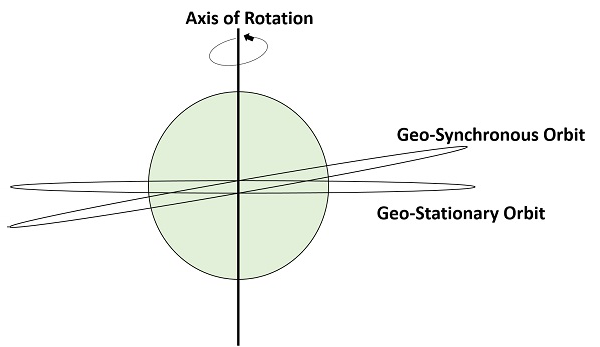
Megjegyzés – Minden geostacionárius pálya geoszinkron pálya. De minden geoszinkron pálya NEM geostacionárius pálya.
Médium Föld körüli pályán keringő műholdak
A MEO (Medium Earth Orbit) műholdhálózatok a Föld felszínétől mintegy 8000 mérföldes távolságban keringenek. A MEO műholdról továbbított jelek rövidebb távolságot tesznek meg. Ez jobb jelerősséget jelent a fogadó oldalon. Ez azt mutatja, hogy a vevőoldalon kisebb, könnyebb vevőterminálok használhatók.
Mivel a jel rövidebb utat tesz meg a műhold felé és a műholdról, kisebb az átviteli késleltetés. Az átviteli késleltetés úgy határozható meg, mint az az idő, amely alatt a jel feljut a műholdra és vissza a vevőállomáshoz.
A valós idejű kommunikáció esetében minél rövidebb az átviteli késleltetés, annál jobb lesz a kommunikációs rendszer. Például, ha egy GEO műholdnak 0,25 másodpercre van szüksége egy oda-vissza út megtételéhez, akkor a MEO műholdnak kevesebb mint 0,1 másodpercre van szüksége ugyanehhez az úthoz. A MEO műholdak a 2 GHz-es és a feletti frekvenciatartományban működnek.
Az alacsony Föld körüli pályán keringő műholdak
Az alacsony Föld körüli pályán keringő műholdakat (LEO) elsősorban három kategóriába sorolják, nevezetesen a kis LEO-k, a nagy LEO-k és a Mega-LEO-k közé. A LEO-k 500-1000 mérföldes távolságban keringenek a Föld felszíne felett.
Ez a viszonylag rövid távolság mindössze 0,05 másodpercre csökkenti az átviteli késleltetést. Ez tovább csökkenti az érzékeny és terjedelmes vevőberendezések szükségességét. A kis LEO-k a 800 MHz-es (0,8 GHz-es) tartományban fognak működni. A nagy LEO-k a 2 GHz-es vagy annál magasabb tartományban, a Mega-LEO-k pedig a 20-30 GHz-es tartományban működnek.
A Mega-LEO-khoz kapcsolódó magasabb frekvenciák nagyobb információhordozó kapacitást jelentenek, és lehetővé teszik a valós idejű, kis késleltetésű videoátviteli rendszer megvalósítását.
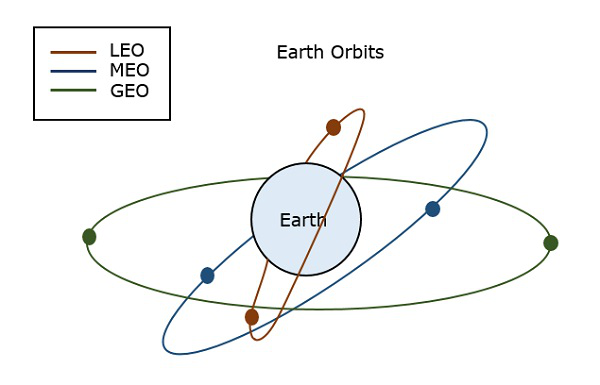
A következő ábra a LEO, MEO és GEO útvonalakat ábrázolja.
