A Concise Introduction to Logic

9.1 Egy történelmi példa

A filozófus David Hume (1711-1776) zseniális szkeptikus empiristaként maradt emlékezetes. Egy személy akkor szkeptikus egy témával kapcsolatban, ha egyrészt nagyon szigorú mércéje van annak, hogy mi számít tudásnak az adott témáról, másrészt úgy véli, hogy nem tudunk megfelelni ezeknek a szigorú mércéknek. Az empirizmus az a nézet, amely szerint elsősorban a tapasztalat, különösen az érzékszerveink tapasztalatai révén szerzünk ismereteket. Az An Inquiry Concerning Human Understanding című könyvében Hume lefekteti a megismerésre vonatkozó elveit, majd azt tanácsolja, hogy takarítsuk ki a könyvtárainkat:

Ha ezekről az elvekről meggyőződve átrohantuk a könyvtárakat, milyen pusztítást kell végeznünk? Ha például kezünkbe vesszük az istentan vagy az iskolai metafizika bármelyik kötetét, kérdezzük meg: Van-e benne a mennyiségre vagy a számra vonatkozó elvont fejtegetés? Nem. Tartalmaz-e bármilyen kísérleti érvelést a tényekre és a létezésre vonatkozóan? Nem. Adjuk hát a lángba, mert nem tartalmazhat mást, csak szofisztikát és illúziót.”

Hume úgy vélte, hogy a tudás egyetlen forrása a logikai vagy matematikai érvelés (amit ő fentebb “mennyiségre vagy számra vonatkozó absztrakt érvelésnek” nevez) vagy az érzéki tapasztalat (“tény- és létanyagra vonatkozó kísérleti érvelés”). Hume arra az érvelésre jut, hogy minden olyan állítás, amely nem az egyik vagy a másik módszerre épül, értéktelen.

Hume érvelését a következőképpen rekonstruálhatjuk. Tegyük fel, hogy t valamilyen téma, amelyről azt állítjuk, hogy ismeretekkel rendelkezünk. Tegyük fel, hogy ezt a tudást nem tapasztalatból vagy logikából szereztük. Magyarul leírva a következő módon rekonstruálhatjuk érvét:

Tudásunk van t-ről, ha és csak akkor, ha a t-ről szóló állításainkat kísérleti érvelésből vagy logikából vagy matematikából tanultuk.

A t-re vonatkozó állításainkat nem tanuljuk meg kísérleti érvelésből.

A t-re vonatkozó állításainkat nem tanuljuk meg logikából vagy matematikából.

Nincs tudásunk t-ről.

Mit jelent ez a “ha és csak ha” kifejezés? A filozófusok szerint ez, és több szinonim kifejezés, gyakran használatos az érvelésben. A “ha és csak” kifejezést egyelőre magyarázat nélkül hagyva, a következő fordítókulcs segítségével leírhatjuk az érvelést a mi tételes logikánk és az angol nyelv keverékében.

P: Tudásunk van t-ről.

Q: A t-ről szóló állításainkat kísérleti érvelésből tanuljuk.

R: A t-re vonatkozó állításainkat logikából vagy matematikából tanultuk.

És így van:

P ha és csak ha (QvR)

¬Q

¬R

¬P

A feladatunk az, hogy logikai nyelvünket kiegészítsük a “ha és csak ha” megfelelőjével. Ezután ki tudjuk értékelni Hume érvének ezt az újrafogalmazását.

9.2 A bikondicionális

Mielőtt bevezetnénk a “ha és csak ha” szinonim szimbólumát, majd lefektetnénk annak szintaktikáját és szemantikáját, egy megfigyeléssel kell kezdenünk. Egy olyan mondat, mint a “P ha és csak akkor, ha Q”, a “P ha Q és P csak akkor, ha Q” kifejezés rövidített formájának tűnik. Ha ezt egyszer észrevettük, nem kell megpróbálnunk az angol nyelv szakértői ismereteink segítségével megfejteni a “ha és csak ha” jelentését. Ehelyett a “ha és csak akkor, ha” jelentését a “ha”, “és” és “csak akkor, ha” már szigorú definícióinak segítségével megismerhetjük. Konkrétan, a “P ha Q és P csak akkor, ha Q” fordítása “((Q→P)^(P→Q))” lesz. (Ha ez nem világos számodra, menj vissza, és nézd át a 2.2. szakaszt.) Most pedig készítsünk egy igazságtáblázatot erre a képletre.

.

P	Q	(Q → P)	(P → Q)	((Q→P)^(P→Q))
T	T	T	T	T	T
T	F	T	F	F
F	T	F	T	F	F
F	F	T	T	T	T

Rendeztük a “ha és csak ha” szemantikáját. Most bevezethetünk egy új szimbólumot erre a kifejezésre. Hagyományosan a kettős nyilat, a “↔”-t használjuk. Most már ki tudjuk fejezni az “↔” szintaxisát és szemantikáját:

Ha Φ és Ψ mondatok, akkor

(Φ↔Ψ)

egy mondat. Az ilyen típusú mondatot tipikusan “bikondicionálisnak” nevezzük.

A szemantikát a következő igazságtáblázat adja.

.

.

Φ	Ψ	(Φ↔Ψ)
T	T	T
T	F	F
F	T	F
F	F	T

A bikondicionálisról szóló beszámolónk egyik kellemes eredménye, hogy lehetővé teszi a logikai ekvivalencia szintaktikai fogalmának tömör magyarázatát. Azt mondjuk, hogy két Φ és Ψ mondat “ekvivalens” vagy “logikailag ekvivalens”, ha (Φ↔Ψ) egy tétel.

9.3. Alternatív mondatok

Az angolban úgy tűnik, hogy több olyan mondat is létezik, amelynek általában ugyanaz a jelentése, mint a bikondicionálisnak. Az alábbi mondatok mindegyikét úgy fordítanánk, hogy (P↔Q).

P ha és csak akkor, ha Q.

P csak akkor, ha Q.

P szükséges és elégséges Q számára.

P egyenértékű Q-val.

9.4 Érvelés a bikondicionálisokkal

Hogyan lehet érvelni a bikondicionálisokkal? Elsőre úgy tűnik, hogy kevés útmutatást nyújt. Ha tudom, hogy (P↔Q), akkor tudom, hogy P és Q igazságértéke megegyezik, de csak ebből a mondatból nem tudom, hogy mindkettő igaz vagy mindkettő hamis. Ennek ellenére kihasználhatjuk a bikondicionális szemantikáját, és megfigyelhetjük, hogy ha a bikondíciót alkotó egyik mondat igazságértékét is ismerjük, akkor a másik mondat igazságértékét is le tudjuk vezetni. Ez egy egyszerű szabályrendszert sugall. Ezek valójában négy szabály lesznek, de egyetlen név, az “ekvivalencia” alá fogjuk őket csoportosítani:

és

és

és

Mi van, ha ehelyett egy bikondíciót akarunk megmutatni? Itt visszatérhetünk ahhoz a belátáshoz, hogy a bikondicionális (Φ↔Ψ) egyenértékű ((Φ→Ψ)^(Ψ→Φ)). Ha mind a (Φ→Ψ), mind a (Ψ→Φ) feltételét be tudnánk bizonyítani, akkor tudnánk, hogy a (Φ↔Ψ) feltételnek igaznak kell lennie.

Ezt a szabályt nevezhetjük “bikondíciónak”. A következő formája van:

(Φ→Ψ)

(Ψ→Φ)

(Φ↔Ψ)

Ez azt jelenti, hogy gyakran, amikor egy bikondicionális bizonyítása a célunk, két feltételes levezetést vállalunk, hogy két feltételest származtassunk, majd használjuk a bikondicionális szabályt. Vagyis sok bikondicionális bizonyítás a következő formájú:

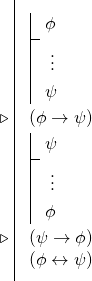
9.5 Visszatérve Hume-hoz

Most megnézzük, hogy képesek vagyunk-e bizonyítani Hume érvét. Adott most az új kétfeltételes szimbólum, a három premisszánkkal kezdhetjük a közvetlen bizonyítást.

Már megfigyeltük, hogy szerintünk (QvR) hamis, mert ¬Q és ¬R. Bizonyítsuk be tehát ¬(QvR). Ezt a mondatot a rendelkezésünkre álló premisszák mellett közvetlenül nem lehet bizonyítani; és feltételes bizonyítással sem lehet bizonyítani, mivel nem feltételes. Próbálkozzunk tehát egy közvetett bizonyítással. Úgy véljük, hogy ¬(QvR) igaz, ezért feltételezzük ennek tagadását, és megmutatjuk az ellentmondást.

Hume érve, legalábbis ahogyan rekonstruáltuk, érvényes.

Hume érve megalapozott? Az, hogy megalapozott-e, a fenti első premisszától függ (mivel a második és harmadik premissza elvonatkoztatások valamilyen t témáról). Legkonkrétabban attól az állítástól függ, hogy valamiről csak abban az esetben van tudásunk, ha azt kísérlettel vagy logikával ki tudjuk mutatni. Hume azt állítja, hogy bizalmatlanok kell lennünk – sőt, el kell égetnünk azokat a szövegeket, amelyek olyan állításokat tartalmaznak, amelyek nem kísérletből és megfigyelésből vagy logikából és matematikából származnak. De gondoljunk csak erre az állításra: akkor és csak akkor van tudásunk egy t témáról, ha a t-re vonatkozó állításainkat kísérletből ismerjük meg, vagy a t-re vonatkozó állításainkat logikából vagy matematikából ismerjük meg.

Hume kísérletekkel fedezte fel ezt az állítást? Vagy a logika révén fedezte fel? Milyen sorsra jutna Hume könyve, ha megfogadnánk a tanácsát?

9.6. Néhány példa

Segítségünkre lehet néhány olyan tétel bizonyítása, amelyek a bikondíciót használják, hogy szemléltessük, hogyan érvelhetünk a bikondícióval.

Itt egy hasznos elv. Ha két mondatnak ugyanaz az igazságértéke, mint egy harmadik mondatnak, akkor ugyanaz az igazságértékük, mint egymásnak. Ezt úgy fogalmazzuk meg, hogy (((P↔Q)^(R↔Q))→(P↔R)). A kétfeltételes érvelés szemléltetésére bizonyítsuk be ezt a tételt.

Ez a tétel egy feltételes tétel, tehát feltételes levezetést igényel. A feltételes tétel következménye bikondicionális, így várhatóan két feltételes levezetésre lesz szükségünk, egy a (P→R) és egy az (R→P) bizonyításához. A bizonyítás így fog kinézni. Tanulmányozzuk át alaposan.

Előtte már említettük azokat az elveket, amelyeket Augustus De Morgan (1806-1871) matematikushoz kötünk, és amelyeket ma “De Morgan-törvényeknek” vagy “De Morgan-egyenértékűségeknek” nevezünk. Ezek annak felismerése, hogy ¬(PvQ) és (¬P^¬Q) egyenértékűek, valamint hogy ¬(P^Q) és (¬Pv¬Q) egyenértékűek. Ezeket most a bikondíciókkal tudjuk kifejezni. A következők logikánk tételei:

(¬(PvQ)↔(¬P^¬Q))

(¬(P^Q)↔(¬Pv¬Q))

E tételek közül a másodikat bizonyítjuk. Ez talán a legnehezebb bizonyítás, amit eddig láttunk; egymásba ágyazott közvetett bizonyításokat igényel, és elég nagy ügyességet abban, hogy megtaláljuk, mi lesz a vonatkozó ellentmondás.

9.7 A tételek használata

Logikánk minden mondata szemantikai értelemben háromféle lehet. Vagy tautológia, vagy ellentmondásos mondat, vagy kontingens mondat. A “tautológiát” (olyan mondat, amelynek igaznak kell lennie) és az “ellentmondásos mondatot” (olyan mondat, amelynek hamisnak kell lennie) már definiáltuk. Az esetleges mondat olyan mondat, amely nem tautológia és nem ellentmondásos mondat. A kontingens mondat tehát olyan mondat, amely lehet igaz, de lehet hamis is.

Itt van egy példa mindkét mondatfajtára:

(Pv¬P)

(P↔¬P)

P

Az első egy tautológia, a második egy ellentmondásos mondat, a harmadik pedig kontingens. Ezt egy igazságtáblázat segítségével láthatjuk.

P	¬P	(Pv¬P)	(P↔¬P)	P
T	F	T	F	T
F	T	T	F	F

Megjegyezzük, hogy a tautológia tagadása ellentmondás, egy ellentmondás tagadása tautológia, és egy kontingens mondat tagadása kontingens mondat.

¬(Pv¬P)

¬(P↔¬P)

¬P

P	¬P	(Pv¬P)	¬(Pv¬P)	¬(Pv¬P)	(P↔¬P)	¬(P↔¬P)
T	F	T	F	F	F	T	T
F	T	T	F	F	T

Egy pillanatnyi gondolkodás után kiderül, hogy elég nagy katasztrófa lenne, ha akár egy ellentmondásos mondat, akár egy kontingens mondat lenne a tételes logikánk tétele. Logikánkat úgy terveztük, hogy csak érvényes érveket produkáljon. Azoknak az érveknek, amelyeknek nincsenek előfeltevéseik, megfigyeltük, olyan következtetésekkel kell rendelkezniük, amelyeknek igaznak kell lenniük (ez megint csak abból következik, hogy egy olyan mondat, amely előfeltevések nélkül bizonyítható, bármilyen előfeltevéssel bizonyítható, tehát jobb, ha igaz, függetlenül attól, hogy milyen előfeltevéseket használunk). Ha egy tétel ellentmondásos lenne, akkor tudnánk, hogy hamisat tudunk bizonyítani. Ha egy tétel kontingens lenne, akkor néha be tudnánk bizonyítani egy valótlanságot (vagyis be tudnánk bizonyítani egy olyan mondatot, amely bizonyos feltételek mellett hamis). És mivel a közvetett levezetést mint bizonyítási módszert elfogadtuk, ebből az következik, hogy ha egyszer egy érvelésben van egy ellentmondás vagy egy ellentmondásos mondat, akkor bármit be tudunk bizonyítani.

A tételek nagyon hasznosak lehetnek számunkra az érvelésben. Tegyük fel, hogy tudjuk, hogy sem Smith, sem Jones nem megy Londonba, és ezért be akarjuk bizonyítani, hogy Jones nem megy Londonba. Ha megengednénk magunknak, hogy De Morgan egyik tételét használjuk, akkor gyorsan elvégezhetnénk az érvelést. Tegyük fel a következő kulcsot:

P: Smith Londonba megy.

Q: Jones Londonba megy.

És a következő érvünk van:

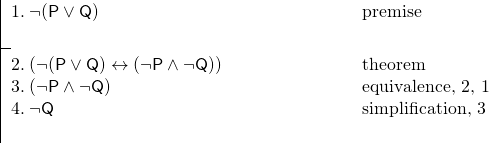
Ezt a bizonyítást nagyon megkönnyítette, hogy a 2. sorban a tételt használtuk.

Ezzel kapcsolatban két dolgot kell megjegyezni. Először is, ezt meg kell engednünk magunknak, mert ha tudjuk, hogy egy mondat egy tétel, akkor tudjuk, hogy ezt a tételt egy albizonyításban be tudjuk bizonyítani. Vagyis a fenti 2. sort helyettesíthetnénk egy hosszú albizonyítvánnyal, amely bizonyítja (¬(P v Q)↔(¬P ^ ¬Q)), amit aztán felhasználhatnánk. De ha biztosak vagyunk abban, hogy (¬(P v Q)↔(¬P ^ ¬Q)) egy tétel, akkor nem kellene ezt a bizonyítást újra és újra elvégeznünk minden egyes alkalommal, amikor használni akarjuk a tételt.

A második probléma, amit fel kell ismernünk, sokkal finomabb. A tételünk formájának végtelen sok mondata létezik, és ezeket is fel kellene tudnunk használni. Például a következő mondatok mindegyike a tételünk bizonyításával (¬(P v Q)↔(¬P ^ ¬Q)) megegyező bizonyítással rendelkezne, csak a betűk lennének különbözőek:

(¬(R v S) ↔ (¬R ^ ¬S))

(¬(T v U) ↔ (¬T ^ ¬U))

(¬(V v W) ↔ (¬V ^ ¬W))

Ez remélhetőleg nyilvánvaló. Vegyük a (¬(P v Q)↔(¬P ^ ¬Q)) bizonyítását, és ebben a bizonyításban cseréljük ki a P minden példányát R-re és a Q minden példányát S-re, és akkor megkapjuk a (¬(R v S)↔(¬R ^ ¬S)) bizonyítását.

De itt van valami, ami talán kevésbé nyilvánvaló. Az alábbi tételek mindegyikére úgy gondolhatunk, mint a (¬(P v Q)↔(¬P ^ ¬Q)) tételhez hasonlóra.

(¬((P^Q) v (R^S))↔(¬(P^Q) ^ ¬(R^S)))

(¬(T v (Q v V))↔(¬T ^ ¬(Q v V))

(¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬(R→¬Q)))

Például, ha veszünk egy (¬(P v Q)↔(¬P ^ ¬Q)) bizonyítást, és P minden kezdeti példányát (Q↔P)-re, Q minden kezdeti példányát pedig (¬R→¬Q)-ra cseréljük, akkor megkapnánk a (¬((Q↔P) v (¬R→¬Q))↔(¬(Q↔P) ^ ¬(¬R→¬Q)) tétel bizonyítását.)

Ezt a felismerést kétféleképpen ragadhatnánk meg. Megállapíthatjuk a metanyelvünk tételeit, és megengedhetjük, hogy ezeknek legyenek példányai. Így a (¬(Φ v Ψ) ↔ (¬Φ ^ ¬Ψ)) tételt vehetnénk metanyelvi tételnek, amelyben minden Φ-et egy mondattal, minden Ψ-et pedig egy mondattal helyettesíthetnénk, és így egy tétel adott példányát kapnánk. Egy másik lehetőség, hogy megengedjük, hogy egy tételből más tételeket is előállíthassunk helyettesítéssel. Az egyszerűség kedvéért ezt a második stratégiát választjuk.

A szabályunk a következő lesz. Ha egyszer bebizonyítottunk egy tételt, bármikor hivatkozhatunk rá egy bizonyításban. Azzal igazoljuk, hogy az állítás egy tétel. A tételben szereplő bármely atomos mondat helyettesítését bármely más mondattal akkor és csak akkor engedjük meg, ha a tételben szereplő atomos mondat minden egyes kezdeti példányát ugyanezzel a mondattal helyettesítjük.

Mielőtt egy példát megvizsgálnánk, hasznos, ha felsorolunk néhány hasznos tételt. Nyelvünknek végtelenül sok tétele van, de ez a tíz gyakran nagyon hasznos. Néhányat már bizonyítottunk. A többit gyakorlatként be lehet bizonyítani.

T1 (P v ¬P)

T2 (¬(P→Q) ↔ (P^¬Q))

T3 (¬(P v Q) ↔ (¬P ^ ¬Q))

T4 ((¬P v ¬Q) ↔ ¬(P ^ Q))

T5 (¬(P ↔ Q) ↔ (P ↔ ¬Q))

T6 (¬P → (P → Q))

T7 (P → (Q → P))

T8 ((P→(Q→R)) → ((P→Q) → (P→R)))

T9 ((¬P→¬Q) → ((¬P→Q) →P))

T10 ((P→Q) → (¬Q→¬P))

A tételek használatának előnyét néhány példával fogjuk érzékeltetni. Tekintsünk egy másik érvet, a fentiekre építve. Tudjuk, hogy sem az nem igaz, hogy ha Smith Londonba megy, akkor Berlinbe megy, sem az nem igaz, hogy ha Jones Londonba megy, akkor Berlinbe megy. Be akarjuk bizonyítani, hogy nem igaz, hogy Jones Berlinbe megy. A kulcsunkhoz a következőket adjuk hozzá:

R: Smith Berlinbe fog menni.

S: Jones Berlinbe fog menni.

És a következő érvünk van:

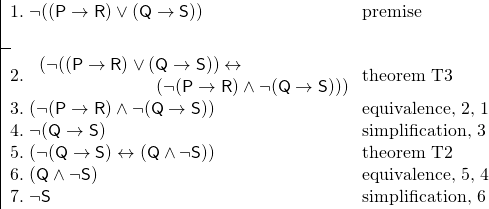
A tételek felhasználásával ez a bizonyítás sokkal rövidebb lett, mint amilyen egyébként lehetne. Emellett a tételek gyakran könnyebben követhetővé teszik a bizonyítást, mivel a tételeket tautológiáknak ismerjük fel – olyan mondatoknak, amelyeknek igaznak kell lenniük.

9.8. feladatok

1. Bizonyítsuk be, hogy a következő érvek mindegyike érvényes.

1. Tételek: P, ¬Q. Következtetés: ¬(P↔Q).
2. Premisszák: (¬PvQ), (Pv¬Q). Következtetés: (P↔Q).
3. Elhelyezkedések: (P↔Q), (R↔S) . Következtetés: ((P^R)↔(Q^S)).

1. Bizonyítsuk be a következő tételek mindegyikét.

1. T1
2. T2
3. T5
4. T6
5. T7
6. T8
7. T9
8. ((P^Q)↔¬(¬Pv¬Q))
9. ((P→Q)↔¬(P^¬Q))

1. Szokásos köznyelvi nyelven írja meg saját érvényes érvét legalább két premisszával, amelyek közül legalább az egyik bikondicionális. Az érvelésed csak egy bekezdés legyen (ne mondatok rendezett listája vagy bármi más, ami formális logikának tűnik). Fordítsd le tételes logikára, és bizonyítsd be, hogy érvényes.
2. Normál köznyelvi angol nyelven írj egy saját érvényes érvet legalább két premisszával, és egy olyan konklúzióval, amely két feltételes. Az érvelésed csak egy bekezdés legyen (ne mondatok rendezett listája vagy bármi más, ami formálisan logikának tűnik). Fordítsd le tételes logikára, és bizonyítsd be, hogy érvényes.