Forståelse af eksponenter og kvadratrødder
Læringsmål
– Vurdere udtryk, der indeholder eksponenter.
– Skrive gentagne faktorer ved hjælp af eksponentiel notation.
– Finde en kvadratrod af et perfekt kvadrat.
Introduktion
Eksponenter giver en særlig måde at skrive gentagne multiplikationer på. Tal, der skrives på denne måde, har en særlig form, hvor hver del giver vigtige oplysninger om tallet. Ved at skrive tal ved hjælp af eksponenter kan man også spare en masse plads. Den omvendte operation af multiplikation af et tal med sig selv kaldes at finde kvadratroden af et tal. Denne operation er nyttig i forbindelse med problemer om arealet af et kvadrat.
Forståelse af eksponentiel notation
Eksponentiel notation er en særlig måde at skrive gentagne faktorer på, f.eks. 7 – 7. Eksponentiel notation består af to dele. Den ene del af notationen kaldes basen. Basen er det tal, der ganges med sig selv. Den anden del af notationen er eksponenten, eller potensen. Det er det lille tal, der står højt oppe til højre for basen. Eksponenten, eller potensen, fortæller, hvor mange gange basen skal bruges som faktor i multiplikationen. I eksemplet kan 7 – 7 skrives som 72, 7 er basen, og 2 er eksponenten. Eksponenten 2 betyder, at der er to faktorer.
72 = 7 – 7 = 49
Du kan læse 72 som “syv i kvadrat”. Det skyldes, at multiplikation af et tal med sig selv kaldes “kvadrering af et tal”. På samme måde kaldes det at hæve et tal til en potens af 3 for at “kubikere tallet”. Du kan læse 73 som “syv kubikeret.”
Du kan læse 25 som “to til femte potens” eller “to til fem potenser af fem”. Du kan læse 84 som “otte i fjerde potens” eller “otte i fjerde potens”. Dette format kan bruges til at læse ethvert tal, der er skrevet i eksponentiel notation. Faktisk kan 63, selv om 63 oftest læses som “seks i kubik”, også læses som “seks i tredje potens” eller “seks i tredje potens.”
For at finde værdien af et tal, der er skrevet i eksponentiel form, skal du omskrive tallet som gentagen multiplikation og udføre multiplikationen. To eksempler er vist nedenfor.
|
Eksempel |
||||
|
Problem |
Find værdien af 42. |
|||
|
4 er grundleddet. 2 er eksponenten. |
En eksponent betyder gentagen multiplikation. Basen er 4; 4 er det tal, der ganges. Eksponenten er 2; Det betyder, at man bruger to faktorer af 4 i multiplikationen. |
|||
|
42 = 4 – 4 |
Opskriv det igen som gentagen multiplikation. |
|||
|
4 – 4 = 16 |
Multiplicer. |
|||
|
Svar 42 = 16 |
||||
|
Eksempel |
||||
|
Problem |
Find værdien af 25. |
|||
|
2 – 2 – 2 – 2 – 2 – 2 – 2 |
Opnyt 25 som gentagen multiplikation. Basen er 2, det tal, der ganges. Eksponenten er 5, det antal gange, der skal bruges 2 i multiplikationen. |
|||
|
2 – 2 – 2 – 2 – 2 – 2 – 2 4 – 2 – 2 – 2 – 2 8 – 2 – 2 – 2 16 – 2 32 32 |
Udfør multiplikation. |
|||
|
Svar 25 = 32 |
||||
Søg værdien af 43.
A) 12
B) 64
C) 256
D) 43
Skrivning af gentagen multiplikation ved hjælp af eksponenter
Skrivning af gentagen multiplikation i eksponentiel notation kan spare tid og plads. Overvej eksemplet 5 – 5 – 5 – 5 – 5 – 5. Vi kan bruge eksponentiel notation til at skrive denne gentagne multiplikation som 54. Da 5 bliver ganget, skrives det som basis. Da basen anvendes 4 gange i multiplikationen, er eksponenten 4. Udtrykket 5 – 5 – 5 – 5 – 5 kan omskrives i eksponentiel notation som 54 og læses: “5 i fjerde potens” eller “5 i 4’s potens.”
For at skrive gentagen multiplikation af det samme tal i eksponentiel notation skal du først skrive det tal, der multipliceres, som base. Tæl derefter, hvor mange gange dette tal bruges i multiplikationen, og skriv dette tal som eksponenten. Sørg for at tælle tallene, ikke multiplikationstegnene, for at bestemme eksponenten.
|
Eksempel |
||||
|
Problem |
Skriv 7 – 7 – 7 – 7 i eksponentiel notation. |
|||
|
7 er basis.
Da 7 bruges 3 gange, er 3 eksponenten. |
Basen er det tal, der ganges, 7. Eksponenten fortæller, hvor mange gange basen ganges. |
|||
Skriv 10 – 10 – 10 – 10 – 10 – 10 – 10 – 10 i eksponentiel notation.
A) 1.000.000
B) 60
C) 105
D) 106
Forståelse og beregning af kvadratrødder
Som du så tidligere, kaldes 52 for “fem i kvadrat”. “Fem i kvadrat” betyder, at man ganger fem med sig selv. I matematikken kalder vi det at gange et tal med sig selv for “kvadrering” af tallet. Vi kalder resultatet af kvadreringen af et helt tal for et kvadrat eller et perfekt kvadrat. Et perfekt kvadrat er et tal, der kan skrives som et helt tal opløftet til en potens af 2. F.eks. er 9 et perfekt kvadrat. Et perfekt kvadratisk tal kan repræsenteres som en kvadratisk form, som vist nedenfor. Vi ser, at 1, 4, 9, 16, 25 og 36 er eksempler på perfekte kvadrater.
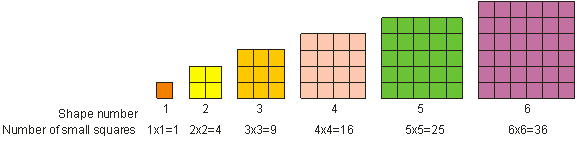

For at kvadrere et tal skal tallet ganges med sig selv. 3 kvadreret = 32 = 3 – 3 = 9.
Nedenfor er der flere eksempler på perfekte kvadrater.
|
1 kvadreret |
12 |
1 – 1 |
1 |
|
2 kvadreret |
22 |
2 – 2 |
4 |
|
3 kvadreret |
32 |
3 – 3 |
9 |
|
4 kvadreret |
42 |
4 – 4 |
16 |
|
5 kvadreret |
52 |
5 – 5 |
25 |
|
6 kvadreret |
62 |
6 – 6 |
36 |
|
7 kvadreret |
72 |
7 – 7 |
49 |
|
8 kvadreret |
82 |
8 – 8 |
64 |
|
9 kvadreret |
92 |
9 – 9 |
81 |
|
10 kvadreret |
102 |
10 – 10 |
100 |
Den omvendte operation af kvadrering af et tal kaldes at finde kvadratroden af et tal. At finde en kvadratrod svarer til at spørge: “Hvilket tal ganget med sig selv vil give mig dette tal?” Kvadratroden af 25 er 5, fordi 5 ganget med sig selv er lig med 25. Kvadratrødder skrives med det matematiske symbol, kaldet et radikalt tegn, der ser således ud: ![]() . “Kvadratroden af 25” skrives
. “Kvadratroden af 25” skrives ![]() .
.
|
Eksempel |
||||
|
Problem |
Find |
|||
|
|
Tænk, hvilket tal gange sig selv giver 81? 9 – 9 = 81 |
|||
|
Svar |
|
|
||
Find ![]() .
.
A) 6
B) 18
C) 72
D) 7
Summary
Exponential notation er en kortfattet måde at skrive gentagen multiplikation af det samme tal på. Et tal skrevet i eksponentiel notation har en base og en eksponent, og hver af disse dele giver oplysninger til at finde værdien af udtrykket. Basen fortæller, hvilket tal der multipliceres gentagne gange, og eksponenten fortæller, hvor mange gange basen anvendes i multiplikationen. Eksponenterne 2 og 3 har særlige navne. Når man hæver en base til en potens af 2, kaldes det at “kvadrere” et tal. Når man hæver en base til en potens af 3, kaldes det at “kubikere” et tal. Det omvendte af kvadrering af et tal er at finde kvadratroden af et tal. For at finde kvadratroden af et tal skal du spørge dig selv: “Hvilket tal kan jeg gange med sig selv for at få dette tal?”