Neutronens henfald
|
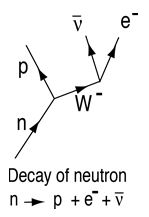
En fri neutron henfalder med en halveringstid på ca. 10,3 minutter, men den er stabil, hvis den indgår i en kerne. Dette henfald er et eksempel på beta-henfald med emission af en elektron og en elektron-antineutrino. Neutronens henfald involverer den svage vekselvirkning, som det fremgår af Feynman-diagrammet til højre. |
 |
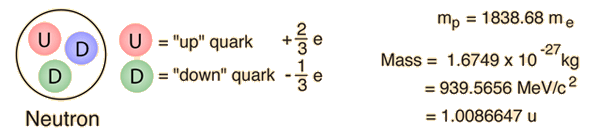
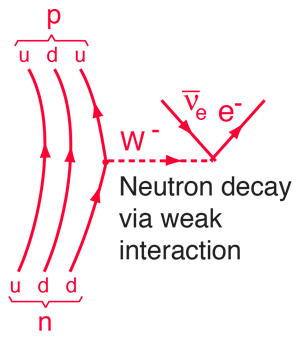 |
Et mere detaljeret diagram over neutronens henfald identificerer det som omdannelsen af en af neutronens down-kvarker til en up-kvark. Det er et eksempel på den slags kvark-transformationer, der er involveret i mange nukleare processer, herunder beta-henfald. |
Neutronens henfald er et godt eksempel på de observationer, som førte til opdagelsen af neutrinoen. En analyse af henfaldets energetik kan bruges til at illustrere de dilemmaer, som de tidlige undersøgere af denne proces stod over for.
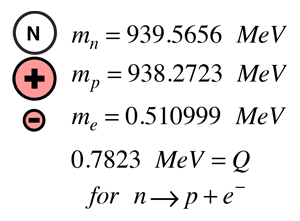 |
Hvis man anvender begrebet bindingsenergi og repræsenterer partiklernes masse ved hjælp af deres hvilemasseenergier, kan energiudbyttet fra neutronens henfald beregnes ud fra partikelmasserne. Energiudbyttet repræsenteres traditionelt ved symbolet Q. Da energi og impuls skal bevares i henfaldet, vil det blive vist, at den lettere elektron vil føre det meste af den kinetiske energi med sig. Med en kinetisk energi af denne størrelsesorden må det relativistiske udtryk for kinetisk energi anvendes. |
Foreløbig antager vi (fejlagtigt), at henfaldet kun involverer proton og elektron som produkter. Energiudbyttet Q ville i så fald blive fordelt mellem proton og elektron. Elektronen vil få størstedelen af den kinetiske energi og vil være relativistisk, men protonen er ikke-relativistisk. Energibalancen er så
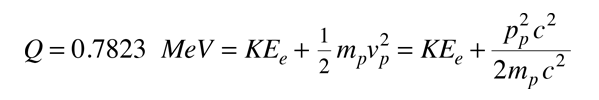
I neutronens hvileramme, kræver bevægelsesbevarelse
og pcelectron kan udtrykkes i form af elektronens kinetiske energi
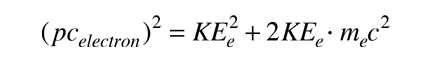 |
Vis |
Energibalancen bliver så
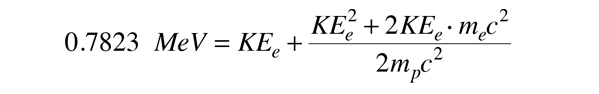
Når man indsætter tallene for denne værdi af Q, ser man, at udtrykket KEe2 er ubetydeligt, så den nødvendige kinetiske energi for elektronen kan beregnes. Den nødvendige kinetiske energi for elektronen for dette topartikelhenfaldsskema er
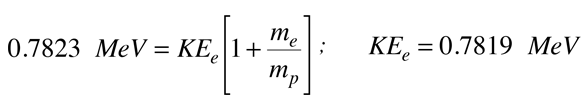
Sådan er elektronens momentum for dette topartikelhenfald tvunget til at være

Momentum og energi for topartikelhenfaldet er tvunget til disse værdier, men det er ikke sådan, naturen opfører sig. De observerede impuls- og energifordelinger for elektronen er som vist nedenfor.
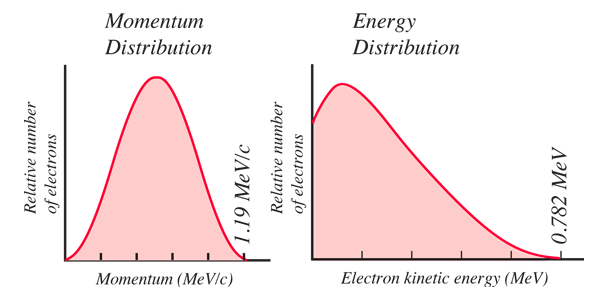
Det faktum, at de elektroner, der blev produceret fra neutronens henfald, havde kontinuerlige energi- og impulsfordelinger, var et klart tegn på, at der blev udsendt en anden partikel sammen med elektronen og protonen. Det måtte være en neutral partikel, og i visse henfald bar den næsten hele energien og impulsen fra henfaldet. Dette ville ikke have været så usædvanligt, hvis det ikke var fordi, at når elektronen havde sin maksimale kinetiske energi, stod den for al den energi Q, der var til rådighed for henfaldet. Der var altså ingen energi tilbage til den anden udsendte partikels masseenergi. De tidlige eksperimentatorer stod over for dilemmaet med en partikel, der kunne bære næsten al energi og impuls fra henfaldet, men som ikke havde nogen ladning og tilsyneladende ingen masse!
Den mystiske partikel blev kaldt en neutrino, men der skulle gå 25 år, før der blev foretaget en entydig eksperimentel observation af neutrinoen af Cowan og Reines. Den nuværende forståelse af neutronens henfald er
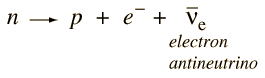
Dette henfald illustrerer nogle af de bevarelseslove, der gælder for partikelhenfald. Protonen i produktet opfylder bevarelsen af baryonantallet, men fremkomsten af elektronen uden ledsagelse ville overtræde bevarelsen af leptonantallet. Den tredje partikel skal være en elektrons antineutrino, for at henfaldet kan opfylde leptonantalets bevarelseskrav. Elektronen har lepton nummer 1, og antineutrinoen har lepton nummer -1.
Eksperimentel påvisning af neutrinos
Stabilitet af neutronen i deuteronen