En satellit er et legeme, der bevæger sig rundt om et andet legeme i en matematisk forudsigelig bane kaldet en bane. En kommunikationssatellit er intet andet end en mikrobølge-repeaterstation i rummet, der er nyttig inden for telekommunikation, radio og tv sammen med internetapplikationer.
En repeater er et kredsløb, der øger styrken af det signal, den modtager, og videresender det. Men her fungerer denne repeater som en transponder, der ændrer frekvensbåndet for det transmitterede signal i forhold til det modtagne.
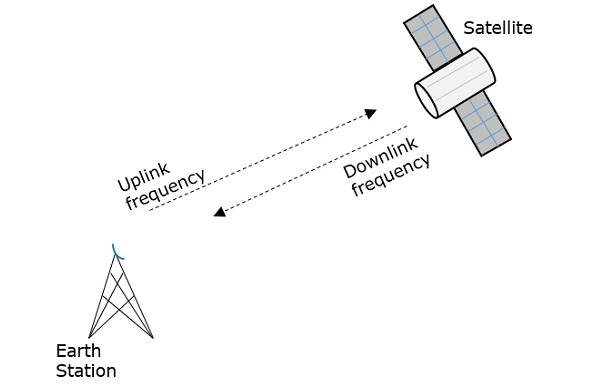
Frekvensen, hvormed signalet sendes ud i rummet, kaldes Uplink-frekvens, mens den frekvens, hvormed det sendes af transponderen, er Downlink-frekvens.
Den følgende figur illustrerer dette koncept tydeligt.
Nu skal vi se på fordele, ulemper og anvendelser af satellitkommunikation.
Satellitkommunikation – Fordele
Der er mange fordele ved satellitkommunikation såsom –
-
Fleksibilitet
-
Let at installere nye kredsløb
-
Distancer kan let dækkes, og omkostningerne er ligegyldige
-
Broadcasting muligheder
-
Alle verdenshjørner er dækket
-
Brugeren kan styre netværket
Satellitkommunikation – ulemper
Satellitkommunikation har følgende ulemper –
-
De indledende omkostninger, såsom segment- og opsendelsesomkostninger, er for høje.
-
Overbelastning af frekvenser
-
Interferens og spredning
Satellitkommunikation – Anvendelsesområder
Satellitkommunikation finder anvendelse på følgende områder –
-
I radioudsendelser.
-
I tv-transmission som f.eks. DTH.
-
I internetapplikationer som f.eks. tilvejebringelse af internetforbindelse til dataoverførsel, GPS-applikationer, internetsurfing osv.
-
Til talekommunikation.
-
Til forsknings- og udviklingssektoren, på mange områder.
-
I militære applikationer og navigationer.
Satellittens orientering i sin bane afhænger af de tre love, der kaldes Keplers love.
Keplers love
Den astronomiske videnskabsmand Johannes Kepler (1571-1630) gav tre revolutionerende love om satellitternes bevægelse. Den bane, som en satellit følger rundt om sin primære (jorden), er en ellipse. Ellipsen har to brændpunkter – F1 og F2, hvoraf jorden er det ene.
Hvis man betragter afstanden fra objektets centrum til et punkt på dets elliptiske bane, kaldes det fjerneste punkt i en ellipse fra centrum for apogee, og det korteste punkt i en ellipse fra centrum for perigee.
Keplers 1. lov
Keplers 1. lov siger, at “enhver planet kredser om solen i en elliptisk bane med solen som et af dens brændpunkter”. Som sådan bevæger en satellit sig i en elliptisk bane med jorden som et af brændpunkterne.
Ellipsens halvstore akse betegnes som “a” og halvmindste akse betegnes som “b”. Derfor kan dette systems excentricitet e skrives som –
$$$e = \frac{\sqrt{a^{2}-b^{2}}}}{a}$$$$
-
Ekcentricitet (e) – Det er den parameter, der definerer forskellen i ellipsens form i forhold til en cirkels form.
-
Semi-majorakse (a) – Det er den længste diameter, der er trukket mellem de to brændpunkter langs centrum, og som berører begge apogeer (de fjerneste punkter i en ellipse fra centrum).
-
Semi-mindre akse (b) – Det er den korteste diameter trukket gennem centrum, som berører begge perigeer (de korteste punkter i en ellipse fra centrum).
Disse er godt beskrevet i følgende figur.
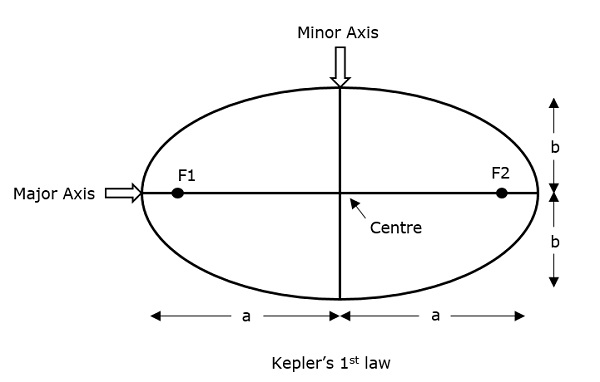
For en elliptisk bane er det altid ønskeligt, at excentriciteten skal ligge mellem 0 og 1, dvs.dvs. 0 < e < 1, for hvis e bliver nul, vil banen ikke længere have elliptisk form, men snarere blive omdannet til en cirkelformet bane.
Keplers 2. lov
Keplers 2. lov siger, at: “For lige store tidsintervaller er det areal, som satellitten dækker, lige stort i forhold til jordens centrum.”
Det kan forstås ved at se på følgende figur.
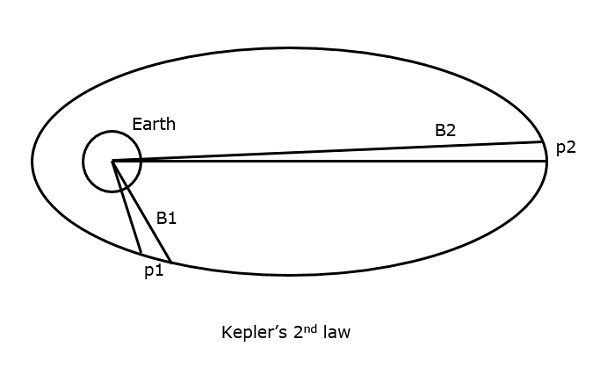
Sæt, at satellitten tilbagelægger p1 og p2 afstande, i samme tidsinterval, så er de arealer B1 og B2, der dækkes i begge tilfælde, henholdsvis lige store.
Keplers 3. lov
Keplers 3. lov siger, at: “Kvadratet af banens periodiske tid er proportionalt med kuben af den gennemsnitlige afstand mellem de to legemer.”
Dette kan matematisk skrives som
$$$T^{2}\:\alpha\:\:a^{3}$$$
Hvilket indebærer
$$$T^{2} = \frac{4\pi ^{2}}}{GM}a^{3}$$$
Hvor $\frac{4\pi ^{2}}}{GM}$ er proportionalitetskonstanten (i henhold til Newtons mekanik)
$$$$T^{2} = \frac{4\pi ^{2}}}{\mu}a^{3} $$$
Hvor μ = jordens geocentriske gravitationskonstant, i.dvs. Μ = 3.986005 × 1014 m3/sek2
$$$1 = \left ( \frac{2\pi}{T} \right )^{2}\frac{a^{3}}}{\mu}$$
$$$1 = n^{2}\frac{a^{3}}}{\mu}\:\:\:\:\Rightarrow \:\:\:\:\:a^{3} = \frac{\mu}{n^{2}}}$$$
Hvor n = satellittens gennemsnitlige bevægelse i radianer pr. sekund
Satellitternes banefunktion beregnes ved hjælp af disse Keplers love.
Sammen med disse er der en vigtig ting, som skal bemærkes. En satellit, når den drejer rundt om jorden, underkastes en trækkende kraft fra jorden, som er gravitationskraften. Desuden oplever den også en vis trækkende kraft fra solen og månen. Der er således to kræfter, der virker på den. De er –
-
Centripetalkraft – Den kraft, der har tendens til at trække et objekt, der bevæger sig i en bane, mod sig selv, kaldes centripetalkraft.
-
Centrifugalkraft – Den kraft, der har tendens til at skubbe et objekt, der bevæger sig i en bane, væk fra sin position, kaldes centrifugalkraft.
Så en satellit skal balancere disse to kræfter for at holde sig i sin bane.
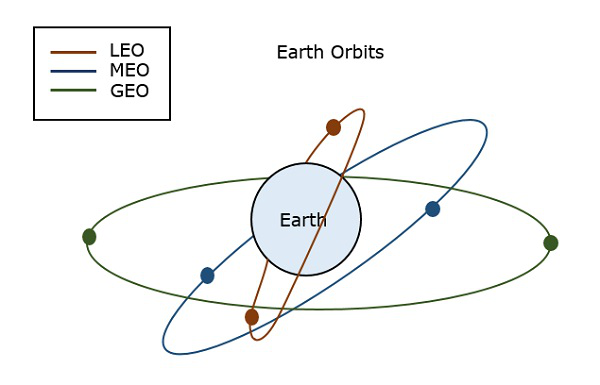
Jordbaner
En satellit, når den opsendes i rummet, skal placeres i en bestemt bane for at give en bestemt måde for dens omdrejning, så den kan bevare tilgængelighed og tjene sit formål, hvad enten det er videnskabeligt, militært eller kommercielt. Sådanne baner, som er tildelt satellitter i forhold til jorden, kaldes jordbaner. Satellitterne i disse baner er jordomløbssatellitter.
De vigtige former for jordbaner er –
-
Geo-synkrone jordbaner
-
Mellemjordbaner
-
Lav jordbaner
Geosynkrone jordbanesatellitter
En geosynkrone jordbanesatellitter
En geo-Synkrone jordomløb (GEO-satellit) er en satellit, der er placeret i en højde på 22,300 miles over Jorden. Denne bane er synkroniseret med en side reel dag (dvs. 23 timer og 56 minutter). Denne bane kan have en hældning og excentricitet. Den må ikke nødvendigvis være cirkulær. Denne bane kan være skæv ved jordens poler. Men den ser stationær ud, når den observeres fra Jorden.
Det samme geosynkrone kredsløb, hvis det er cirkulært og i ækvatorplanet, kaldes det for et geostationært kredsløb. Disse satellitter er placeret 35.900 km (det samme som geosynkrone) over Jordens ækvator, og de bliver ved med at rotere i forhold til Jordens retning (vest til øst). Disse satellitter betragtes som stationære i forhold til jorden, og deraf navnet.
Geo-Stationære jordomløbssatellitter anvendes til vejrudsigter, satellit-tv, satellitradio og andre former for global kommunikation.
Den følgende figur viser forskellen mellem geosynkrone og geostationære baner. Rotationsaksen angiver Jordens bevægelse.
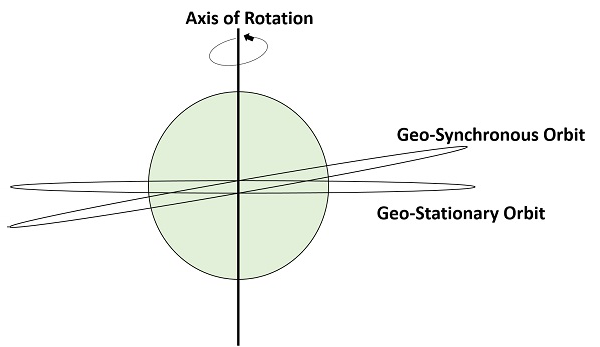
Bemærk – Enhver geostationær bane er en geosynkron bane. Men enhver geosynkron bane er IKKE en geostationær bane.
Medium Earth Orbit Satellitter
Medium Earth Orbit (MEO)-satellitnetværk vil kredse i en afstand på ca. 8000 miles fra jordens overflade. Signaler, der transmitteres fra en MEO-satellit, tilbagelægger en kortere afstand. Det betyder, at signalstyrken i den modtagende ende bliver bedre. Det viser, at der kan anvendes mindre og mere lette modtageterminaler i den modtagende ende.
Da signalet tilbagelægger en kortere afstand til og fra satellitten, er der mindre transmissionsforsinkelse. Transmissionsforsinkelse kan defineres som den tid, det tager et signal at rejse op til en satellit og tilbage ned til en modtagerstation.
For realtidskommunikation gælder det, at jo kortere transmissionsforsinkelse, jo bedre vil kommunikationssystemet være. Hvis en GEO-satellit f.eks. har brug for 0,25 sekunder til en rundrejse, har en MEO-satellit brug for mindre end 0,1 sekunder til at gennemføre den samme rejse. MEO-satellitter opererer i frekvensområdet 2 GHz og derover.
Low Earth Orbit Satellitter
Low Earth Orbit (LEO)-satellitterne er hovedsageligt klassificeret i tre kategorier, nemlig små LEO-satellitter, store LEO-satellitter og Mega-LEO-satellitter. LEO-satellitterne vil kredse i en afstand på 500 til 1000 miles over jordoverfladen.
Denne relativt korte afstand reducerer transmissionsforsinkelsen til kun 0,05 sekunder. Dette reducerer yderligere behovet for følsomt og omfangsrigt modtageudstyr. Små LEO’er vil operere i 800 MHz-området (0,8 GHz). Big LEO’er vil operere i 2 GHz-området eller derover, og Mega-LEO’er opererer i 20-30 GHz-området.
De højere frekvenser, der er forbundet med Mega-LEO’er, giver større informationskapacitet og giver mulighed for videooverførsel i realtid med lav forsinkelse.
Den følgende figur viser vejene for LEO, MEO og GEO.